Типовые звенья лаб1

Безынерционное (усилительное) звено

Дифференциальное уравнение:

Передаточная функция: W(p) = Y(p)/X(p)=k

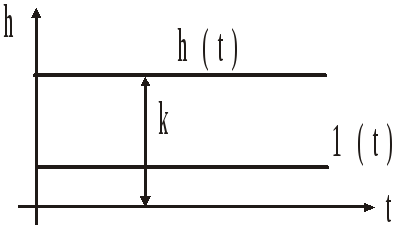
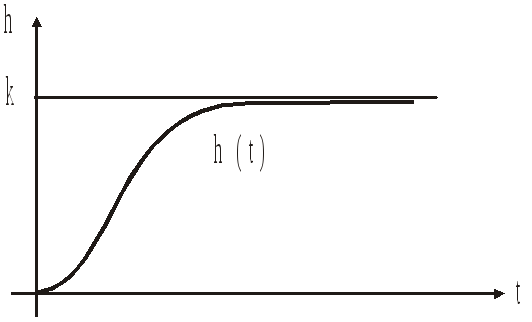
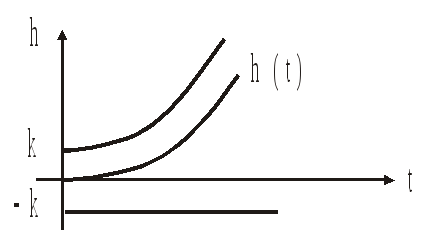
Переходная характеристика:

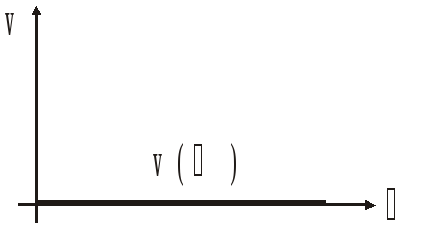
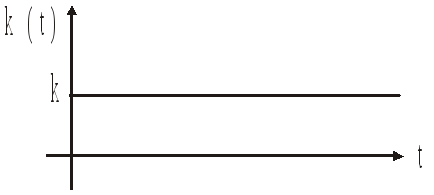
Импульсная переходная характеристика:

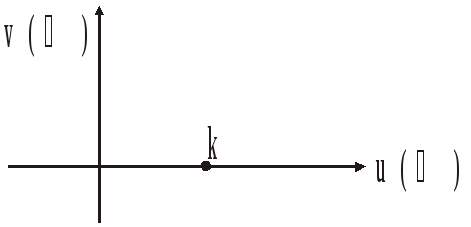
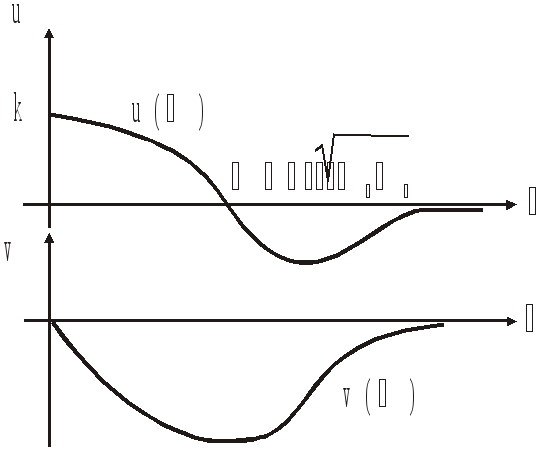
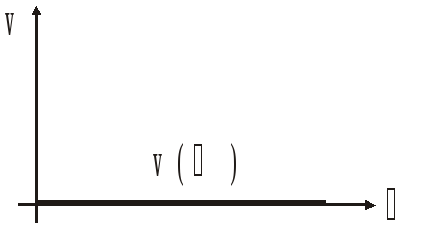
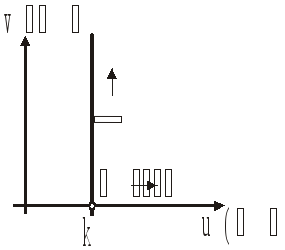
Частотная передаточная функция: W(j)=k; U()=ReW(j)=k; V()=ImW(j)=0

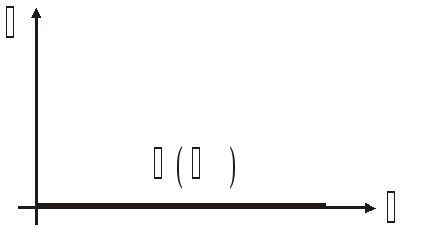
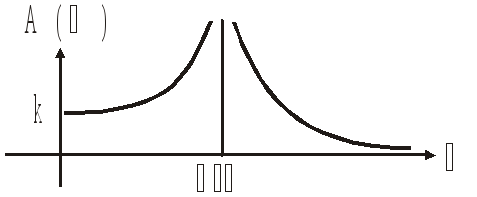
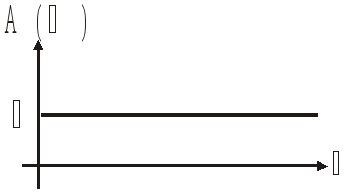
Амплитудная частотная характеристика (АЧХ):

Фазовая частотная характеристика (ФЧХ): () = arg W(j)=0

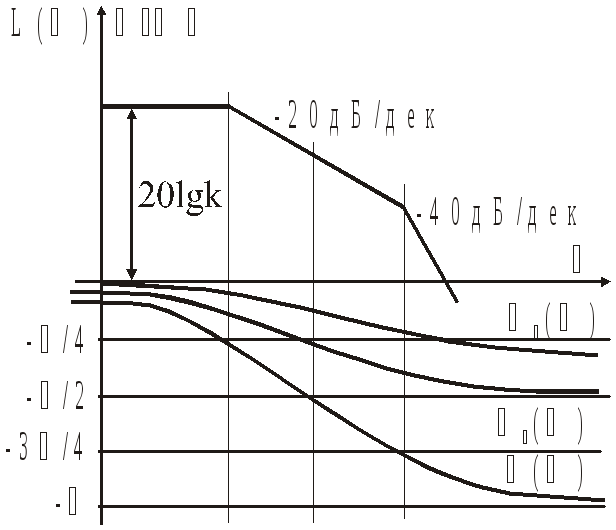
Логарифмическая АЧХ (ЛАЧХ): L() = 20 lgk

Логарифмическая ФЧХ (ЛФЧХ): () = 0

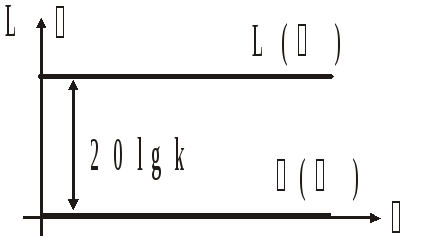
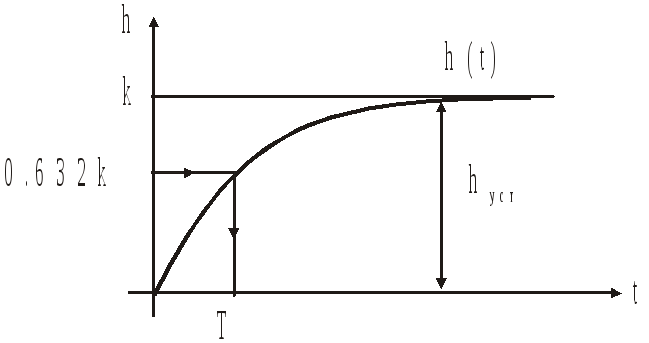
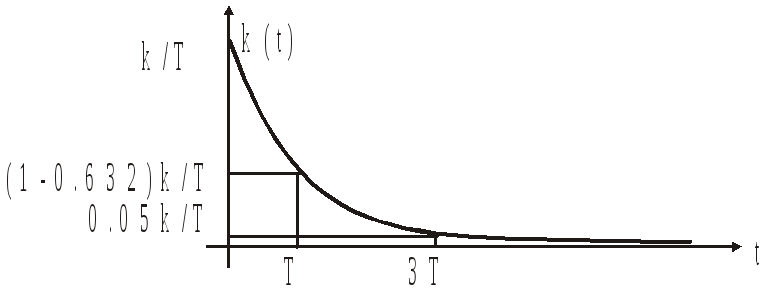
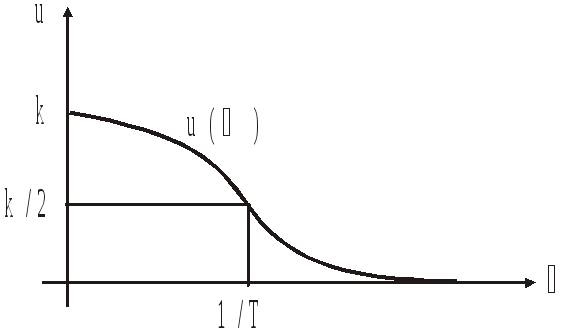
Апериодическое звено 1-го порядка

; ; ; ;

; ; ;

; ; ; ;

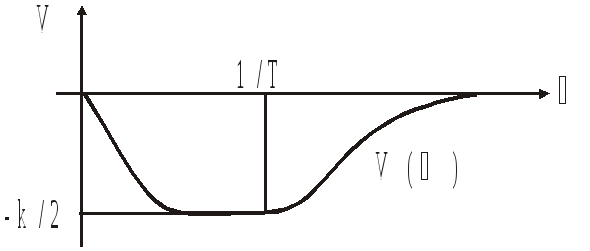
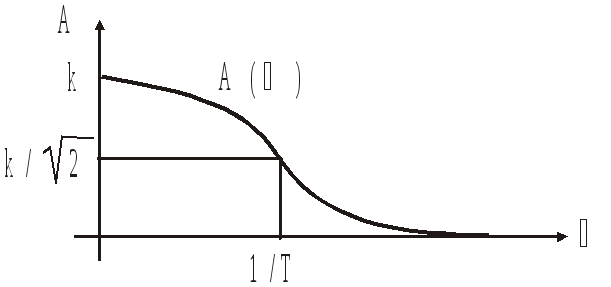
Апериодическое звено 2-го порядка

или ; ;

; ;

;

;

; ;

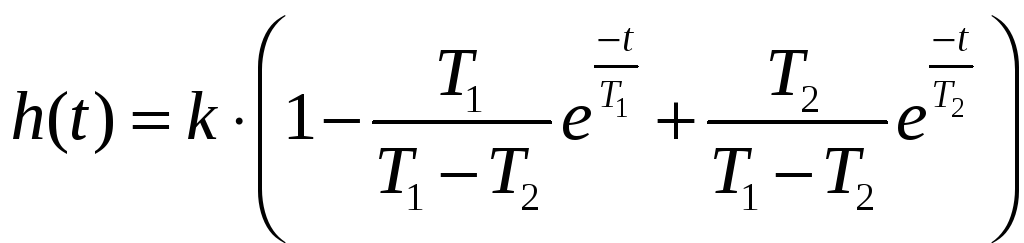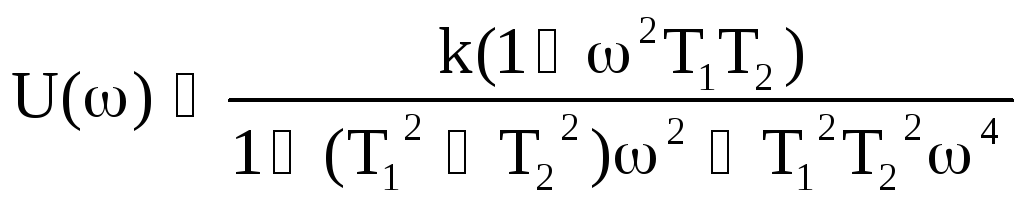c

Колебательное звено

; ;

; ;

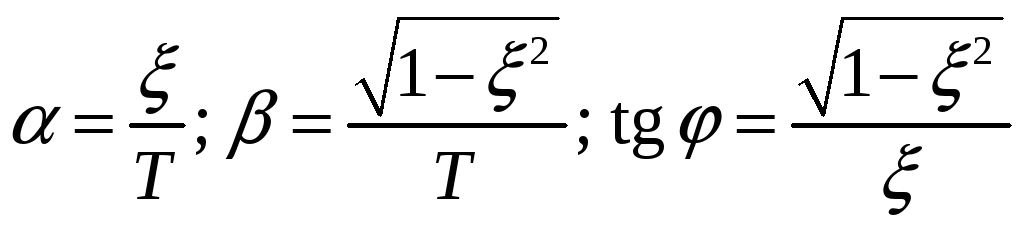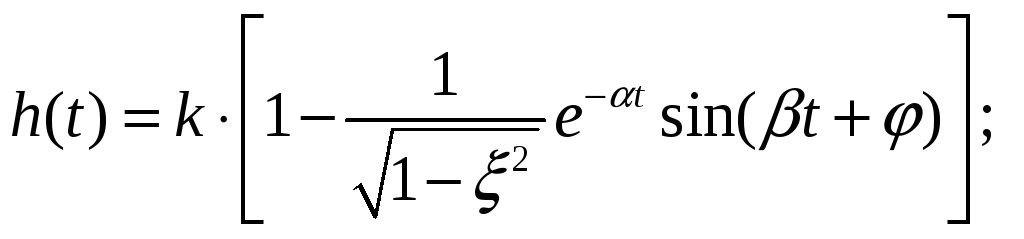
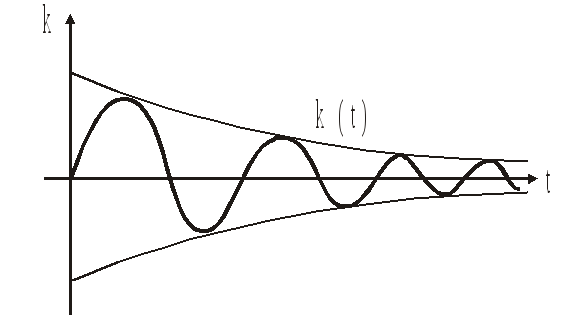
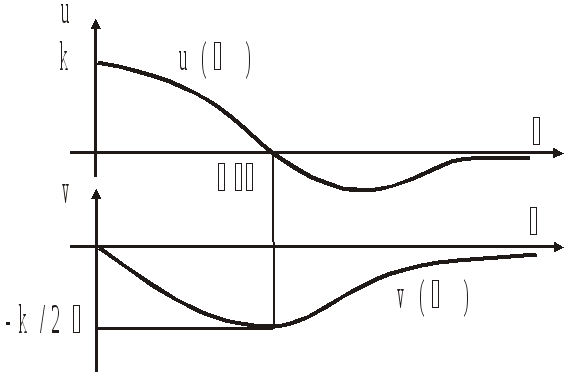
Консервативное звено

; ; ; ;

;;;

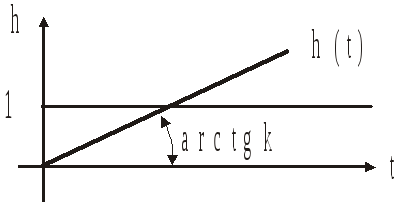
Идеальное интегрирующее звено

; ; ;

; ;

; ;

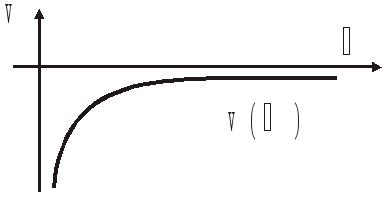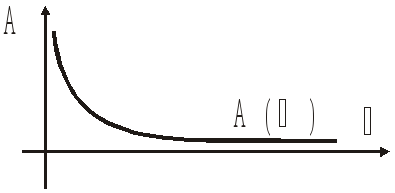
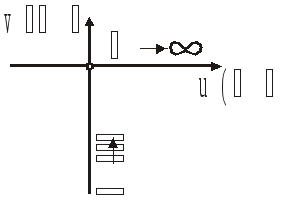
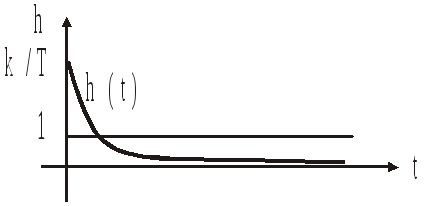
Реальное интегрирующее звено

; ; ;

; ;

; ;

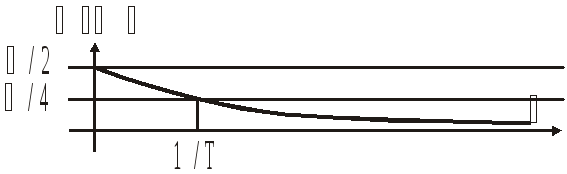
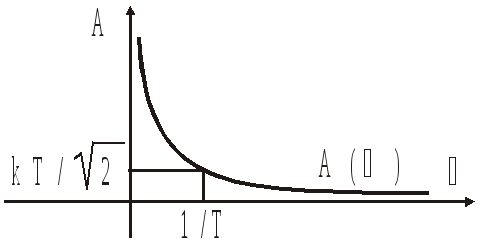
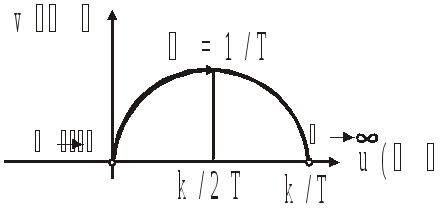
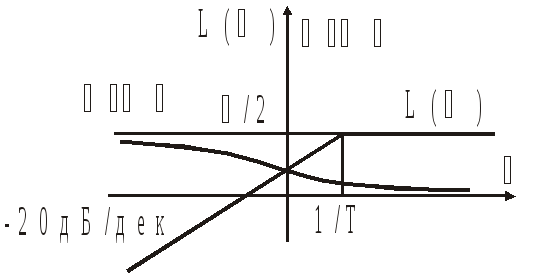
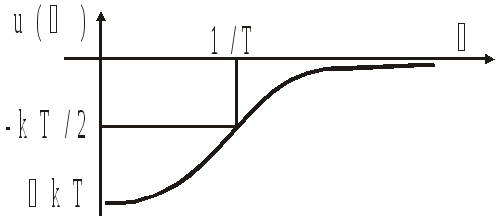
Идеальное дифференцирующее звено

; ; ;

; ;

; ;

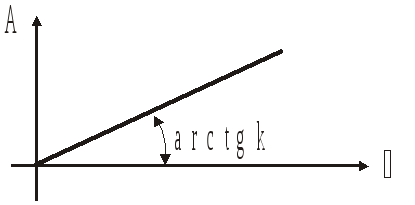
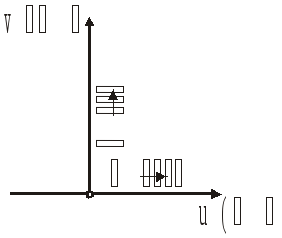
Реальное дифференцирующее звено

; ; ;

; ;

; ;

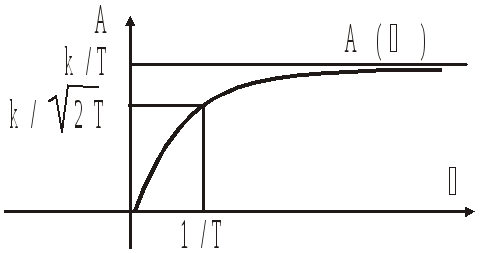Звено предварения (форсирующее звено)

; ; ;

; ;

; ;

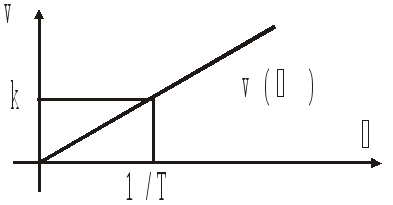
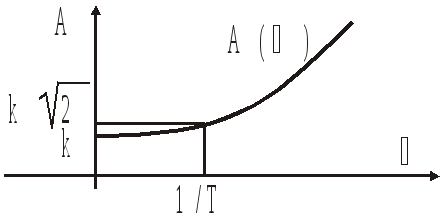
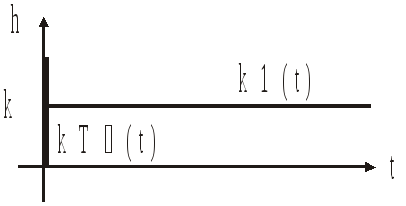
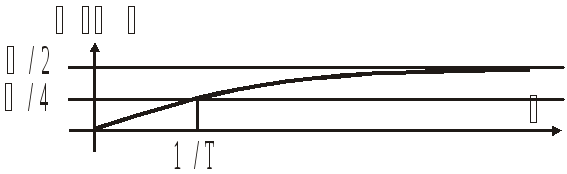
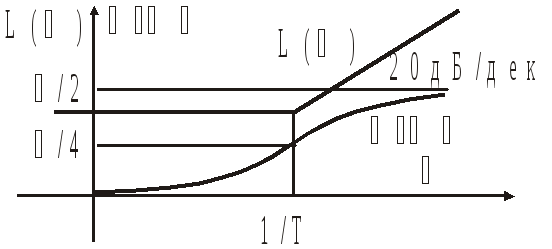
Звено чистого запаздывания

; ; ;

; ;

; ;

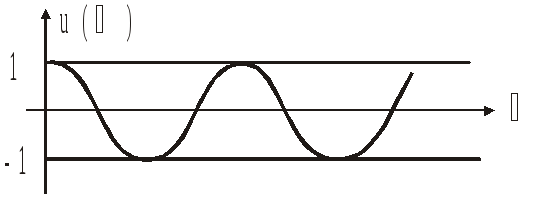
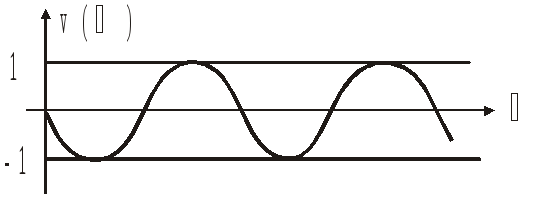
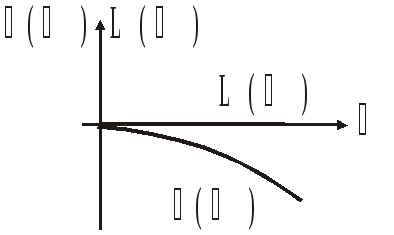
Неминимально-фазовое звено

; ; ;

; ;

; ;

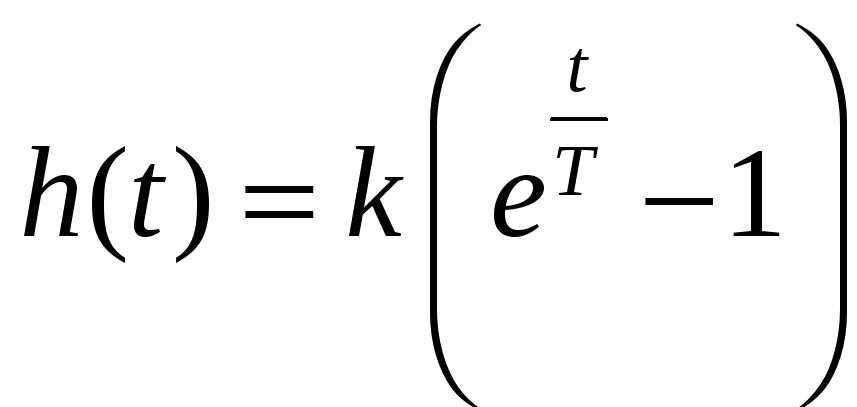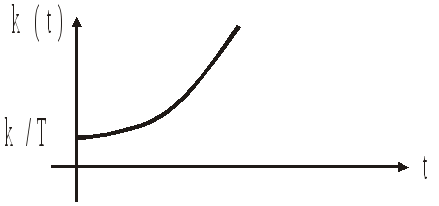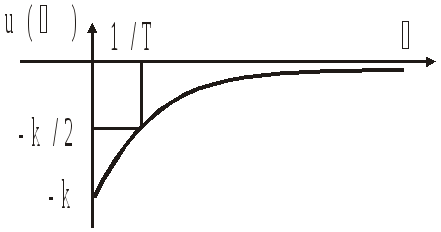
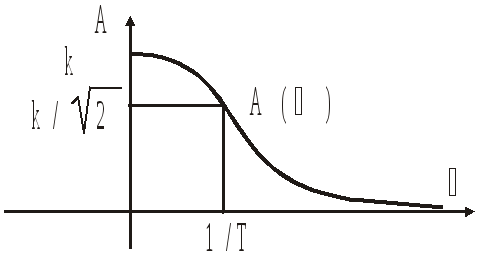
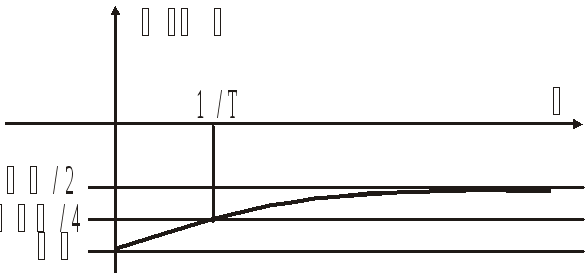
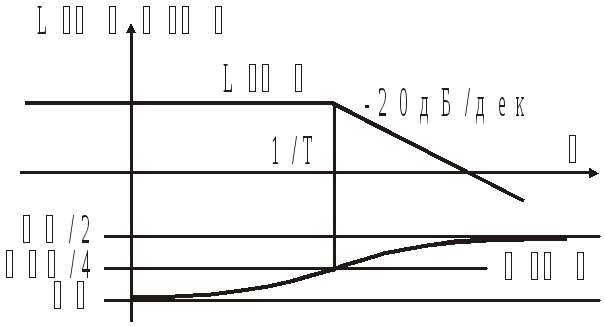
Изодромное звено

; , где ; ;

; ; ; ; ;

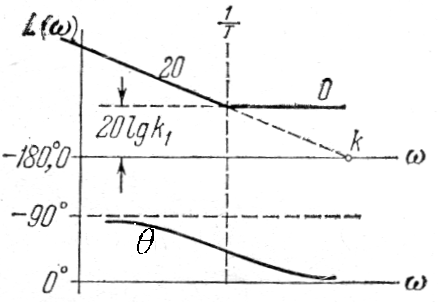
Упругое звено

; ; ; ; ; ; ;

При k=5 T₁=5 T₂=1

h(t)

A()

()

L()

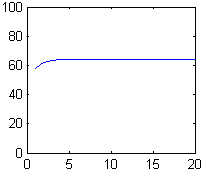
При k=5 T₁=1 T₂=5

h(t)

A()

()

L()