Дипломы2 / Диплом / Чужие дипломы / Колин / MAT

Исследование характеристик транспортных (телекоммуникацион- ных) сетей с централизованным обменом информацией [6].

В этом разделе исследуются централизованные сети обмена дискретной информацией (ЦС) типа "звезда" и "дерево". В частности, определяются распределения пропускных способностей и задержек в передаче информации по каналам ЦС для различных критериев распределения пропускных способностей.

1. Теоретические сведения.

Сети с централизованной структурой.

1. Под сетью с централизованной структурой будем в дальнейшем понимать такую сеть, в которой имеется один центральный узел (НУ) и несколько периферийных узлов (НУ), при этом информация передается только из периферийного узла в центральный. В лабораторной работе исследуются две конфигурации сети с централизованной структурой - "звезда" и "дерево".

Конфигурация типа "звезда" характерна тем, что каждый периферийный узел напрямую соединен с центральным. На рис. 1 приведен пример сети типа "звезда". Центральный узел обозначен номером 0, периферийные 1-4.

Рис. 1.

Рис. 2.

Конфигурация типа "дерево" отличается от "звезды" тем, что периферийный узел может передавать центральному узлу информацию не напрямую, а через более близкий к центральному периферийный узел. При этом каждый периферийный узел соединяется только с одним узлом, периферийным или центральным.

На рис. 2 приведен пример сети типа "дерево". Центральный узел обозначен номером периферийные узлы 1-8.

Линия нумеруется по исходящему узлу, т.е. линия, соединяющая 3-й узел с 1-м будет иметь номер 3.

2. Действующие и проектируемые в настоящее время сети могут быть отнесены к одной из двух групп:

а. Сети с коммутацией каналов, аналогичные телефонным сетям. Здесь установление соединения и выбор маршрута предшествуют началу передачи сообщений. Сообщения передаются только после того, как установлено соединение.

б. Сети с коммутацией сообщений или пакетов. В этом случае не .устанавливается прямое соединение двух абонентов между собой до начала передачи. Сообщения полностью или по частям ( в виде коротких пакетов ) передаются по каналам связи от узла к узлу, образуя очереди. В узлах сети с коммутацией сообщений устанавливаются микро-ЭВМ, которые осуществляют необходимую перекодировку при вводе сообщения в сеть, концентрацию и буферизацию сообщений, выбор маршрута к следующему узлу и т.д. Эти ЭВМ называют программируемыми или удаленными концентраторами или связными процессорами. При этом между взаимодействующими абонентами (терминалами) устанавливается логический или виртуальный канал. В данной работе мы будем исследовать только сети с коммутацией каналов, использующие либо коммутированные либо выделенные (скроссированные) каналы.

Для анализа модели используем методы теории очередей. Рассматриваемая модель обслуживания имеет следующие характеристики:

· процесс поступления сообщений- пуассоновский с интенсивностью l сообщений/с;

· объем буферной памяти не ограничен;

· распределение времени обслуживания- экспоненциальное;

· длина сообщения подчиняется экспоненциальному закону распределения со средним значением 1/m(i) бит;

· сообщения обслуживаются по принципу "первым пришел - первым обслужен".

3. Определение пуассоновского процесса включает следующие предположения:

Рис. 2.

а. Вероятность одного поступления за малый интервал времени (t₂-t₁) равна l*(t₂-t₁)<<1 и не зависит от поступления сообщений в соседние временные интервалы, т.е. вероятность поступления сообщений пропорциональна величине интервала (t₂-t₁).

б. Вероятность того, что за данный интервал времени (t₂-t₁) не поступит ни одного сообщения, равна 1-l*(t₂-t₁).Таким образом, исключается поступление более чем одного сообщения за интервал (t₂-t₁) (при (t₂-t₁) стремящемся к нулю).

в. Вероятность поступления К сообщений за время Т:

(1)

Среднее число сообщений, поступивших за время Т:

(2)

Таким образом, параметр l, являющийся коэффициентом пропорциональности в определении пуассоновского процесса, определяет также интенсивность входного потока.

4. Каждый (i-й) узел сети содержит несколько (N) источников информации, которые, в свою очередь, передают информацию с интенсивностью l(i,j) и средней длиной 1/m(i,j) (j=1...N). Общую интенсивность узла l(i) можно вычислить по формуле:

(3)

Длина сообщения для этого узла будет иметь вид:

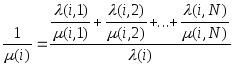(4)

5. Основными факторами при проектировании сети являются время задержки и стоимость.

Так как в данной лабораторной работе принято допущение, что стоимость прямо пропорциональна пропускной способности линии, то при проектировании возникает проблема выбора пропускных способностей каналов связи, т.е. определения такого значения пропускной способности каждого канала сети, при котором обеспечивался бы заданный уровень обслуживания (заданное время задержки).

Для выбора пропускных способностей могут быть использованы следующие критерии:

· критерий равномерного распределения;

· критерий пропорционального распределения;

· критерий "корень квадратный";

· минимаксный критерий.

а. Критерий равномерного распределения. Пропускная способность С распределяется поровну между всеми линиями, независимо от интенсивности трафика, проходящего по каждой линии. В этом случае пропускная способность каждой линии С(i)==С/N , где N - количество линий, С - общая пропускная способность.

б. Критерий пропорционального распределения. Пропускная способность С(i) каждого канала пропорциональна интенсивности потока сообщений l(i) этого канала, т.е.:

(5)

в. Критерий "корень квадратный". Пропускная способность каждого канала вычисляется по формуле:

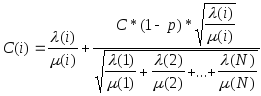(6)

где P - величина загрузки всей сети, причем:

Среднее время задержки для этих критериев вычисляется по формуле:

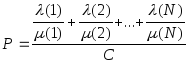(7)

г. Минимаксный критерий.

Пропускная способность:

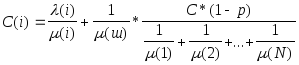(8)

Соответствующее время задержки для каждой линии определяется равенством:

(9)

2. Расчет на примере сети с конфигурацией типа дерево.

Пусть в сети имеется один центральный узел и три периферийных (рис. 3), каждый из узлов содержит по четыре терминала. Каждый терминал выдает сообщение длинной 1/m₁ = 56 бит/сообщений, каждая станция, кроме центральной, выдает сообщение длинной 1/m₂ = 136 бит/сообщение.

Решим обратную задачу, т.е. для известной скорости передачи между станциями (32 Кбит/с) и скоростью передачи между станцией и терминалом (64 Кбит/с) найдем необходимые интенсивности сообщений станций и терминалов, чтобы обеспечить данную скорость передачи.

Рис. 3.

Поскольку все терминалы выдают сообщения с одинаковой интенсивность l1, тогда преобразовав формулу 3 получим общую интенсивность станции

Пропускная способность по критерию пропорционального распределения С₂ между станциями 8 Кбит/с, следовательно для известных 1/m₂ и С₂ получим, что l₂ £ 60,2 сообщений/с и l₁ £ 36,5 сообщений/с.

Для критерия «корень квадратный»:

р1 = 0,1248;

С₁ = 16 Кбит/с;

Т₁ = 3,9 мс;

р2 = 0,9994;

С₂ = 8 Кбит/с;

Т₂ = 6,7 мс.

Минимаксный критерий:

С₁ = 16 Кбит/с;

Т₁ = 3,9 мс;

С₂ = 8 Кбит/с;

Т₂ = 6,9 мс.

Результаты расчетов показали, что для данной конфигурации сети необходимо опрашивать терминалы с интенсивностью не более 36,5 раз в секунду, а станции не более 60,2 раз в секунду. При этом будет поддерживаться заданные скорости передачи между станцией и станцией, между станцией и терминалом с временем задержки 6,9 мс и 3,9 мс, соответственно.