Лабораторные / АТПП-3-Лабораторные / Метод параллельного программирования

Метод параллельного программирования

Применяется, если

Пример:

; ;

Метод последовательного программирования

Применяется, когда САУ представлена структурной схемой с использованием типовых звеньев. В этом случае каждое из типовых звеньев заменяется соответствующей ему схеме переменных состояния, построенной методом прямого программирования.

П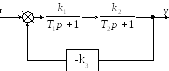 ример:

Области применения методов программирования схем переменных состояния

Если САУ представлена передаточной функцией высокого порядка и не раскладывается на простые составляющие, то применяется метод прямого программирования.

Если САУ представлена структурной схемой, в которой м.б. выделены типовые звенья, то применяется метод последовательного программирования, кроме того метод последовательного программирования применяется в том случае, если для использования САУ необходимы не только выходные, но и промежуточные переменный.

Схема переменных состояния построенная методом последовательного программирования имеет наиболее ясный физический смысл.

Схема переменных состояния, построенная методом параллельного программирования применяется тогда, когда W(p) представлена в виде  типовых передаточных функций. В этом случае матрица коэффициентов имеет наиболее простой вид, сто облегчает дальнейшее исследование САУ

Матрицы перехода

;

Т – некоторое время (не постоянная времени)

(Т) – матрица перехода

Матрицу перехода можно получить тремя способами:

• Аналитический

• Разложением в ряд

• По схеме переменных состояния

Аналитический способ получения матрицы перехода

(1)

Применим к уравнению (1) преобразование Лапласа:

, где

- квадратная матрица;

- единичная матрица

Ф(Т)

Пример:

; ;

;

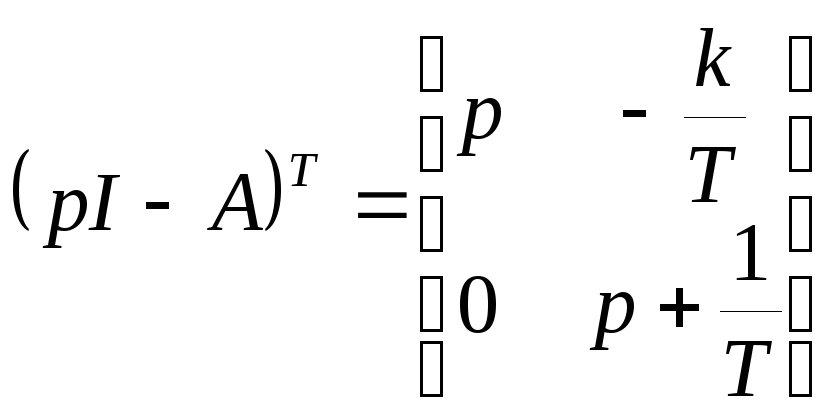
Получение матрицы перехода разложением в ряд

Решением дифференциального уравнения (1) является:

Вычислять до тех пор, пока:

Получение матрицы перехода по схеме переменных состояния

,

Предположим, что ;

Элемент , матрицы перехода Ф определяется по схеме переменных состояния как реакция i-й переменной на ед. ступеньку, поданную на j-ю переменную при прочих нулевых начальных условиях.

С точки зрения использования различных способов получения Ф(Т), предпочтение отдается аналитическому способу и способу разложения в ряд, при этом аналитический способ дает явную формулу определения матрицы перехода, что позволяет использовать данную матрицу при различных значениях.

Если величина t является фиксированной, то удобнее использовать метод разложения в ряд, как наиболее экономичный