Лабораторные / АТПП-3-Лабораторные / Анализ систем методом пространства состояний95

Анализ систем методом пространства состояний.

1. Основные понятия и термины метода пространства состояний.

Метод пространства состояний предполагает использование методов матричного исчисления и векторного анализа.

Произвольная непрерывная система автоматического управления представляется в виде черного ящика:

Состояние системы характеризуется как минимальная информация о системе, необходимая для определения поведения системы в будущем при известных входных воздействиях.

Вектор входа (совокупность сигналов управления):

или

Входные сигналы управления преобразуются в объекте управления, образуя векторное пространство состояний, описываемое вектором состояний:

или

Совокупность выходных переменных образует векторное пространство выхода системы и описывается вектором выхода:

или

Разделение переменных в формализуемой системе на переменные входа, выхода и состояния произвольно и определяется проектировщиком с позиции удобства формализации и наглядности избранных матриц, отражающих взаимодействие сигналов в системе.

Наиболее распространенной формой представления дифференциальных уравнений в векторно-матричной форме в терминах пространства состояний является матричное уравнение:

- уравнение состояния системы.

Задача найти V(t).

Находим решение с помощью операционного исчисления.

Прямое преобразование Лапласа:

- решение уравнения в операционном виде.

Обратное преобразование Лапласа:

,

где - показывает реакцию системы в точке i при подаче на

j-ый элемент единичного воздействия.

где V(t) – расширенный вектор-столбец системы, включает в себя переменные входа и переменные состояния:

А – матрица коэффициентов дифференциальных уравнений.

Пример: уравнение линейной системы в векторно-матричной форме:

- вектор состояния системы,

- матрица коэффициентов.

Начальное состояние системы выражается вектором начальных условий:

,

где 0⁺ - отражает начальные условия с положительным смещением по оси времени.

Расчет переходного процесса по методу пространства состояний сводится к следующему:

1. производим преобразование Лапласа с учетом вектора начальных условий:

   ,

   где I – единичная матрица:

   .

2. Обозначим через Ф(р), где Ф(р) – изображение матрицы перехода. Выполнив обратное преобразование Лапласа, получим:

.

Наиболее сложные процедуры определения динамики системы следующие:

1. обращение матрицы ;

2. определение элементов матрицы Ф(t).

Способы определения матрицы перехода (Ф(t)).

I способ – аналитический способ.

Пример составления структурной схемы по передаточной функции:

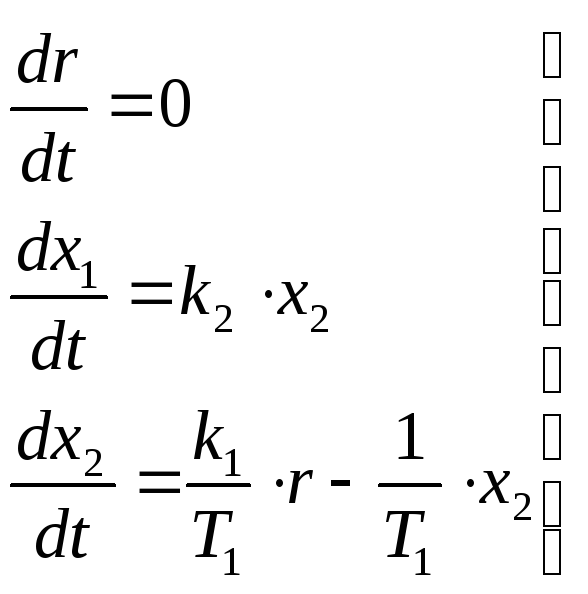
Пример составления структурной схемы по передаточной функции.

Дана передаточная функция:

Показать переход от W(p) и схем переменных состояний

Определитель

Находим присоединенную матрицу перехода:

Преобразование L^-1 – обратное преобразование Лапласа:

Зададимся конкретными числами: Т=Т₀=1

к₁=2; к₂=1; Т₁=4;

Дано:

Расчет:

припасовывание

Один раз рассчитав Ф(T₀) можно узнать состояние системы в любой момент времени:

II способ определения матрицы Ф(t)

Способ основан на численном разложении матрицы в степенной ряд:

где А – матрица коэффициентов дифференциального уравнения;

Т – фиксированное время разложения.

Данный способ легко реализуется на ЭВМ.

III способ определения матрицы перехода Ф(р).

Схемы переменных состояния используются в двух аспектах: расчет элементов изображения матрицы перехода Ф(р) и получение формализованной формы линейных дифференциальных уравнений, необходимых при расчете системы средствами ЭВМ.

Определение элементов изображения Ф(р) основано на уравнении:

Развернув матрицы поэлементно, получим:

Для координаты

Принимаем нулевые начальные условия по всем координатам, за исключением одной , определим

Это сделали для того, чтобы установить физический смысл элемента матрицы перехода или соответствующего ему изображения:

элемент матрицы перехода (Ф(р)) есть реакция системы в точке i при возбуждении системы, т.е. при подаче на вход j-го интегратора одного импульсного сигнала.

Метод переменных состояний

Пример:

1,2,3 – номера интеграторов.

Определим элементы матрицы Ф(р):

Элемент матрицы усть W(p) на участке между входом j-го интегратора и выходом i-го интегратора.

Пример вычислений.

Расчет :

Пример 2.

Определение нормализованной формы дифференциальных уравнений (необходимо для расчета систем методом пространства состояний с помощью ЭВМ)

Данный раздел имеет особую актуальность, т.к. в практике проектирования автоматизированных систем конструктор имеет в качестве первичной информации об объекте регулирования структурную схему.

Используя рассмотренные методики преобразования, можно способом последовательного программирования построить схему переменных состояния на основе которой строится нормализованная система дифференциальных уравнений.

Рассмотрим методику на примере:

схема переменных состояний САР

На входе любого интегратора схемы может быть выделена производная интегрируемой переменной. В свою очередь производная определяется суммой сигналов, поступающих на вход интегратора. С учетом этих закономерностей можно определить производные на входах всех интеграторов системы, что и составит в итоге систему уравнений.

Избрав вектор переменных состояния в виде:

Определим систему уравнений для приведенной схемы:

и соответствующую ей матрицу,

которая необходима для расчета Ф(р) на ЭВМ.

Применение метода пространства состояний для расчета дискретных систем.

Метод пространства состояний оказывается наиболее эффективным в задачах анализа и синтеза дискретных систем автоматического управления. Рассмотрим системы с использованием в качестве управляющих устройств микропроцессорных средств. Наиболее распространенным является вариант работы микропроцессора со ступенчатой диаграммой управляющего сигнала, что в соответствии с классификацией дискретных систем ТАУ рассматривается как вариант системы с амплитудной модуляцией.

Обобщенная функциональная схема:

Здесь микропроцессор (МП) представлен как ключ с фиксатором, а объект управления – произвольной непрерывной системой с передаточной функцией W(р).

При обсуждении особенности математического описания дискретных величин с помощью аппарата пространства состояний, необходимо ввести понятие интервала дискретности T₀.

Внутри интервала дискретности МП производится обработка алгоритма управления, по окончании которой обеспечивается прерывание и изменение информации, определяющей уровень последующего дискрета сигнала управления.

Момент изменения информации – момент квантования.

Описание системы автоматического управления возможно как внутри интервала дискретности, так и в точках квантования.

Внутри интервала дискретности для времени система описывается векторно-матричным уравнением:

решение которого аналогично решению для непрерывных систем и имеет вид:

где - вектор расширенный, переменных состояний;

- матрица перехода системы;

- начальные условия, определенные на предыдущем интервале квантования.

При условии вычисляется состояние системы в точке квантования:

.

Далее происходит срабатывание ключей и изменение информации в дискретной части системы, тем самым изменяются начальные условия для расчета движения системы.

Следует отметить, что для большинства систем, при правильном шаге квантования, достаточно обеспечить расчет системы в точках квантования (т.к. расчет движения системы внутри интервалов квантования является нецелесообразным).

Расчет дискретной системы ведется методом припасовывания, т.е. рассчитывается состояние системы на предыдущем интервале квантования, определяются начальные условия в точке , затем определяется состояние системы в точке соответственно уравнению:

Рассмотрим методику определения начальных условий в точках квантования, которая базируется на основе уравнений переходных состояний.

Уравнения переходных состояний определяют связь между переменными в момент замыкания ключа и являются алгебраическими уравнениями.

Пример дискретной системы:

где - момент срабатывания импульсного элемента.

На основе этих уравнений определяется матрица ключей В:

Данная матрица используется для определения состояния системы в точках квантования:

.

Данное уравнение является уравнением переходных состояний в матричной форме.

Непрерывная часть системы в рассматриваемом примере описывается нормализованными дифференциальными уравнениями, определенных по схеме переменных состояния:

По данным уравнениям находим матрицу коэффициентов А:

Рассчитываем расширенную матрицу перехода Ф(Т₀).

Имея Ф(Т₀) и В, можно производить расчет состояния дискретной системы последовательно в точках квантования:

.

Вводим подстановку: ,

где - дискретная матрица перехода.

В итоге получаем:

Уравнение является алгоритмом анализа дискретной системы в точках квантования.

Пример в числах.

Дифференциальными уравнениями описываем систему внутри интервала квантования, а в моменты квантования систему описывают уравнениями переходных состояний.

, т.к. сигнал ступенчатый и он внутри интервала дискретности постоянен.

Для себя: