3. Расчет установившегося режима работы сар по заданной максимальной допустимой ошибке системы с неединичной обратной связью

Пусть априорная информация о входном сигнале сведена к минимуму:

1. Максимальное по модулю значение первой производной входного воздействия (максимальная скорость слежения) – ;

2. Максимальное по модулю значение второй производной входного воздействия (максимальное ускорение слежения) – ;

3. Входное воздействие может быть детерминированным или случайным сигналом с любой спектральной плотностью.

Требуется ограничить максимально допустимую ошибку системы управления при воспроизведении полезного сигнала в установившемся режиме работы величиной .

Требование к точности воспроизведения наиболее просто формулируется для гармонического входного воздействия эквивалентного реальному входному сигналу:

в предположении, что амплитуда и частота заданы, а начальная фаза имеет произвольное значение.

Установим связь между допустимой ошибкой воспроизведения входного воздействия и параметрами системы и входного сигнала.

Пусть структурная схема непрерывной САУ сведена к виду (рис.4).

Рис.4.

Ошибка на выходе системы во временной области определяется выражением:

,

где – эталонная (безошибочная) выходная функция.

Можно показать, что вследствие ограничений на скорости и ускорения выходная функция отличается от ступенчатой.

Отобразим последнее выражение в пространство преобразований Лапласа:

.

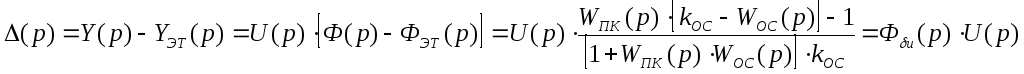Отобразим в пространство преобразований Фурье:

.

В области низких частот (,–постоянные времени цепи обратной связи), тогда

,,

максимальная амплитуда ошибки определяется по выражению:

.

В реальных системах на низких частотах обычно , ибо следует выполнить требование; математическое выражение для определения преобразуется на контрольной частоте () к виду

и для того, чтобы выходная функция воспроизводилась с максимальной ошибкой не более заданной , ЛАЧХ проектируемой системы не должна проходить ниже контрольной точкис координатамии

.

4. Расчет установившегося режима работы статической сау методом предельных переходов

Утверждение

Пусть задана обобщенная структурная схема статической САР:

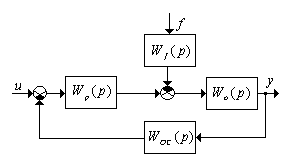
где ,,,, здесь полиномы числителей и знаменателей не содержат множителяp (свободные члены их равны единице),

– передаточный коэффициент регулятора,

– передаточный коэффициент объекта по каналу управления,

– передаточный коэффициент обратной связи,

– передаточный коэффициент объекта по каналу возмущения,

причем в первом приближении статические и динамические передаточные коэффициенты звеньев приняты равными, номинальному входному воздействию соответствует номинальная величина выходной функциипо каналу управления, и пусть заданы величина ступенчатого возмущающего воздействияи– допустимая статическая ошибка по каналу возмущения в % от номинального значения выходной функции.

Тогда передаточные коэффициенты системы по каналам управления и возмущения в установившемся режиме равны статическим передаточным коэффициентам замкнутой системы и определяются по формулам:

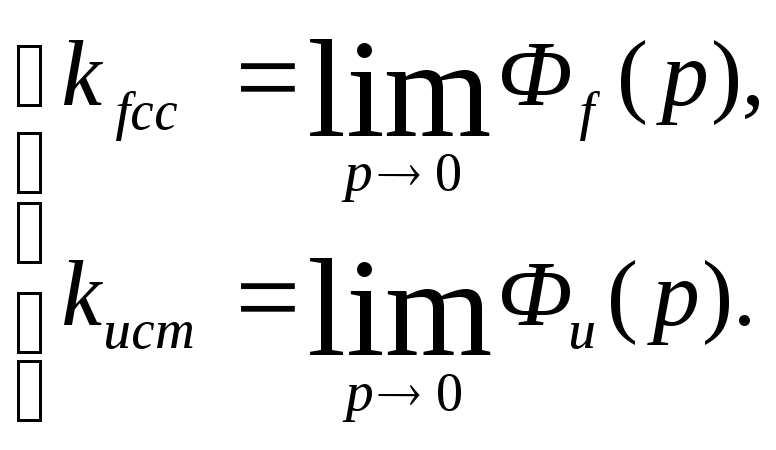(1)

Уравнения статики по каналам управления и возмущения имеют вид

(2)

Передаточные коэффициенты регулятора и цепи обратной связи определяются по выражениям:

(3)