Практическое занятие №12

Тема: «Применение метода фазовых траекторий для анализа и синтеза

нелинейных систем управления »

Литература

1. Лукас В.А. Теория управления техническими системами.-Екатеринбург: Изд-во УГГУ,2005.

2. Филлипс Ч., Харбор Р. Системы управления с обратной связью. – М.: Лаборатория Базовых Знаний, 2001.

3. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПб, Издательство

«Профессия», 2003.

.

Пример содержания отчёта

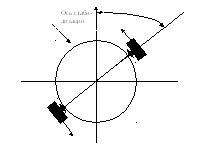
Под действием возмущающих сил спутник поворачивается относительно оси вращения. Предположим , что спутник жёсткий , трение о воздух отсутствует .

Требуется стабилизировать положение спутника относительно оси вращения,

применив систему управления положением спутника с обратной связью по скорости.

- выходная функция

спутник

двигатели

0 - ось вращения

двигатели

- входное воздействие

Вращающий момент, приложенный к спутнику с целью стабилизации положения в пространстве, создаётся парой двигателей.

Уравнение динамики вращательного движения:

,

где – момент инерции спутника,

“ – “ - момент направлен в сторону уменьшения рассогласования (против часовой стрелки).

Преобразуем уравнение к виду

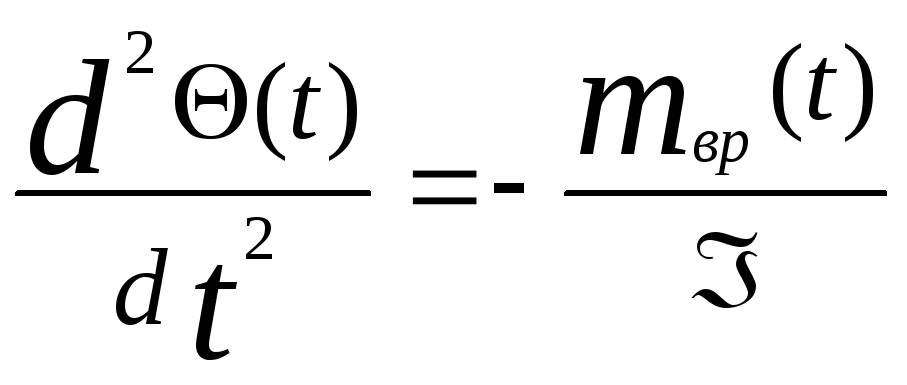, обозначим u(t) =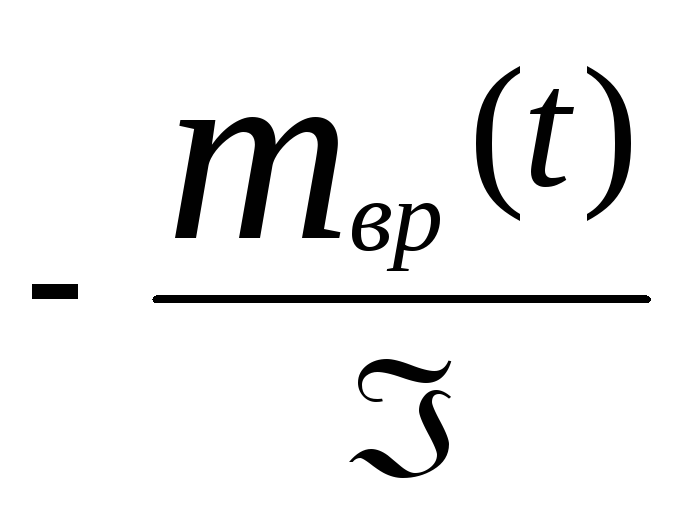 , тогда .

Передаточная функция спутника .

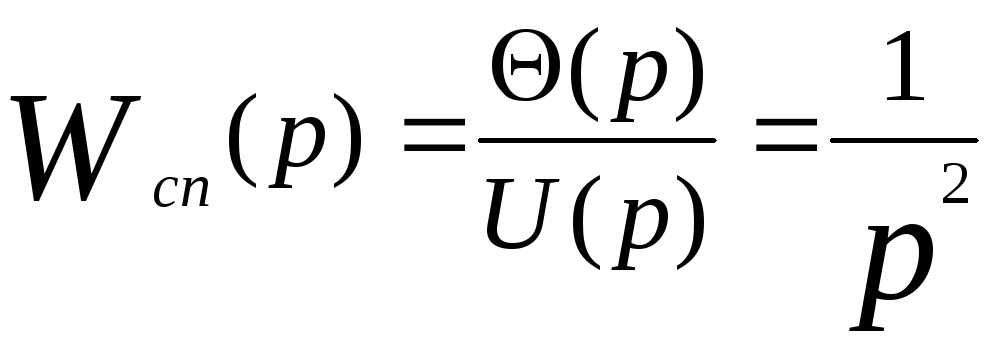Двигатели

- команда на

Мвр/ Спутник выключение

двигателей системы.

g=0 + u(t)

_ _

-Мвр/

Гироскопический датчик скорости

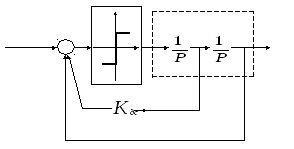
Структурная схема системы стабилизации

Обозначим (t)=y , тогда модель системы в форме переменных состояния примет вид

u-при уменьшении угла поворота спутника

-u–при увеличении угла поворота спутника

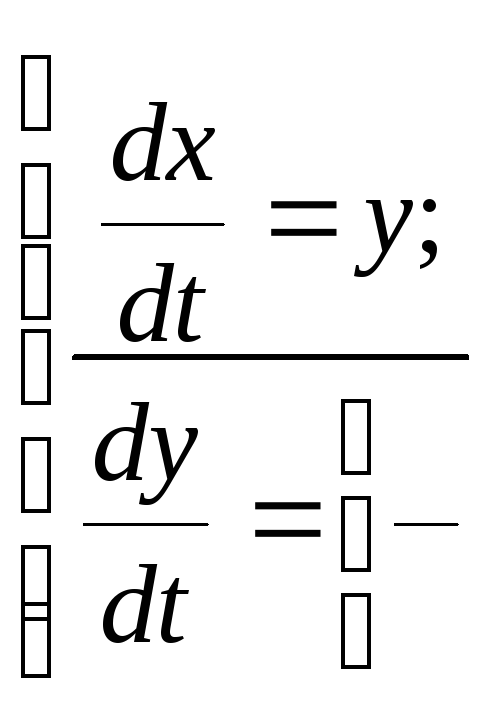- уравнение в форме Коши.

Разделив второе уравнение на первое, получим уравнение фазовых траекторий для области А:

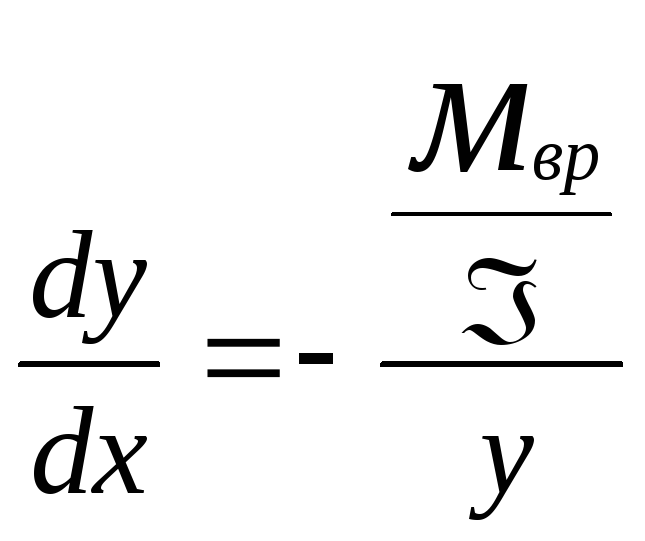, для области Б: .

Следовательно , фазовые траектории представляют собой параболы :

для области А: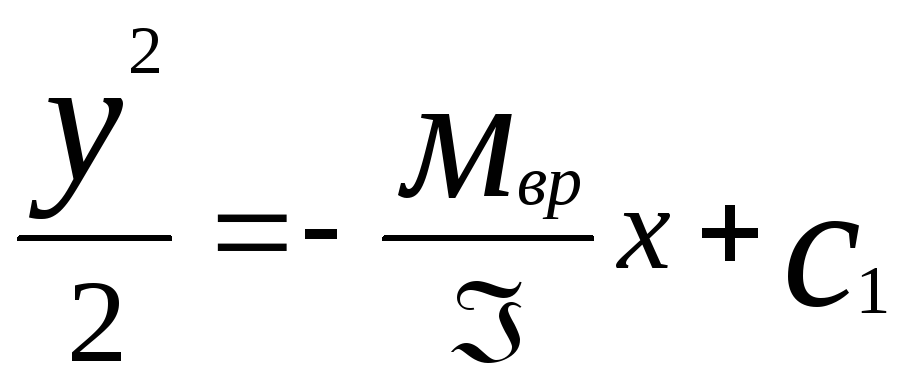 , для области В: ,

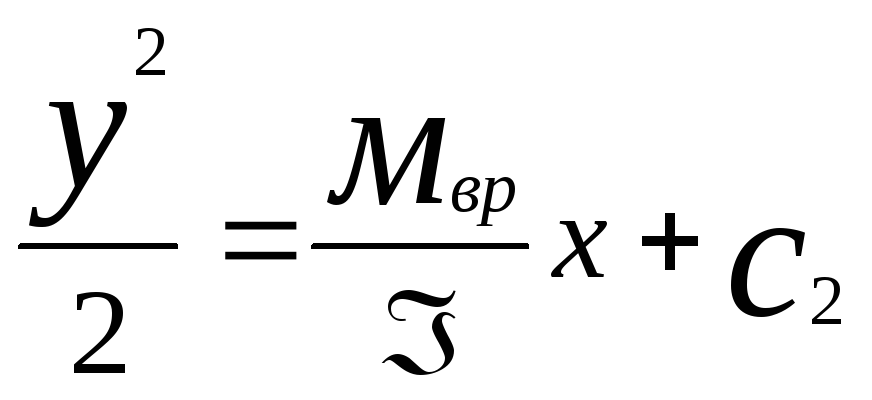при Кдс=0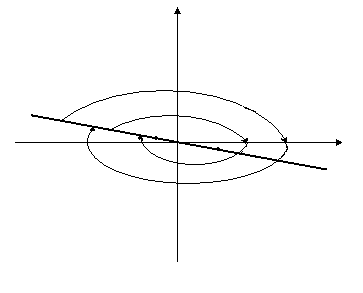

y A - условие переключения

Скользящий режим двигателей системы.

(дребезг)

Фазовые траектории y=; .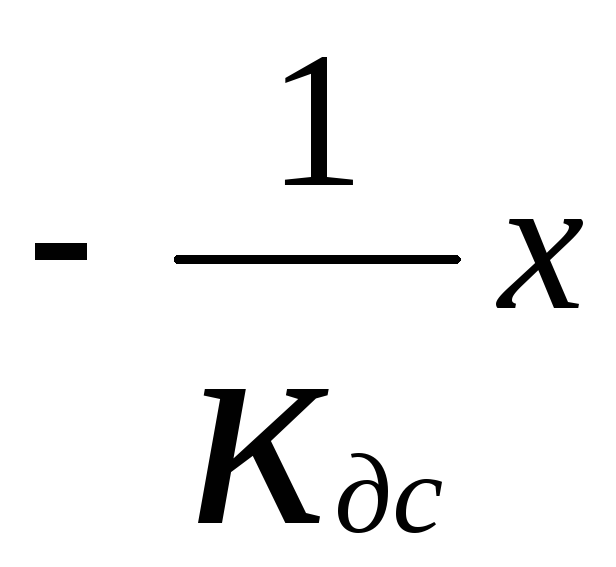

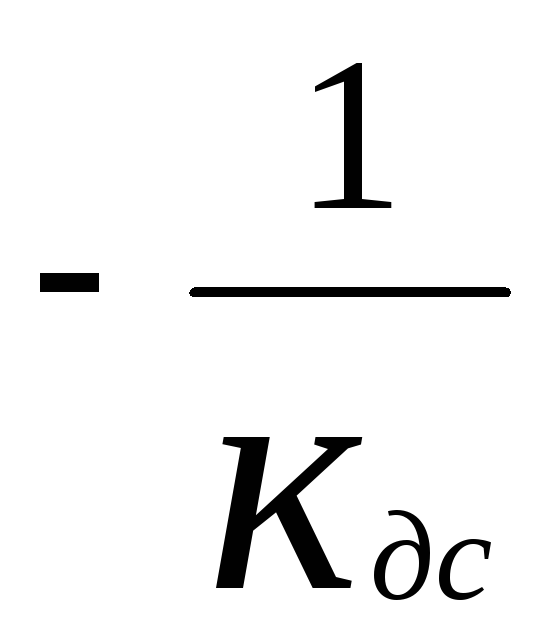М x

N Линия переключения

MN – особый отрезок.

Б

Асимптотически

устойчивый центр

Фазовая плоскость

где C1 определяется из начальных условий : => ) ,

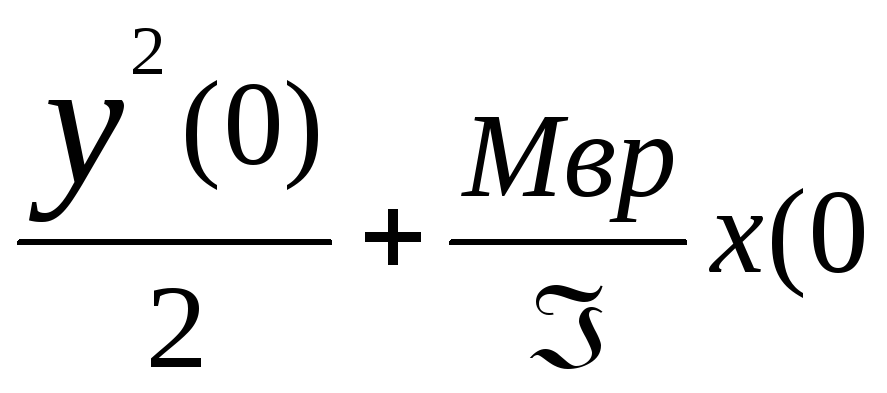аналогично ).

Корректирующая обратная связь аналогична действию ПД – регулятора прямого канала.