Практическое занятие №9

Тема: «Определение изображений решетчатых функций по заданным аналитическим выражениям непрерывных производящих функций. Определение дискретных и псевдочастотных передаточных функций разомкнутых цифро-аналоговых систем»

Литература

1. Лукас В.А. Теория управления техническими системами.-Екатеринбург: Изд-во УГГУ,2005.

2. Бесекерский В. А. Цифровые автоматические системы. – М.: Наука,1976.

3. Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория базовых знаний, 2004.

.

Пример содержания отчёта

Пример 1.

Определить z - изображение единичной ступенчатой решетчатой функции f[nT] при T=1c.

1(t) – производящая функция;

L1(t)=.

; ; .

Используем формулу суммирования убывающей геометрической прогрессии .

Для бесконечно убывающей прогрессии n,

тогда . Знаменатель прогрессии q=z^-1.

Тогда для |z|>1 .

Пример 2.

Задана решетчатая экспонента , где  - постоянная, в общем случае, комплексная величина, T=1c.

;

;

;

;

знаменатель прогрессии q=z^-1.

Для |z| > e^-αT

, где d=e^-αT.

Пример 3.

Пусть - интегратор; , .

.

Тогда .

Чтобы перейти к логарифмическим частотным характеристикам произведем подстановку : , если вместо w подставить , получим псевдочастотную функцию : .

- комплексный передаточный коэффициент интегрирующего звена с фиксатором 0-го порядка.

Свойства :

1. C уменьшением периода дискретизации (T0, =2/T ) характеристика приближается к характеристике непрерывной системы;

2. Предельный фазовый сдвиг равен -, такая замкнутая система приближается к границе устойчивости при больших k.

Пример 4.

Пусть , тогда

,

где .

.

Перейдем к псевдочастотным функциям :

,

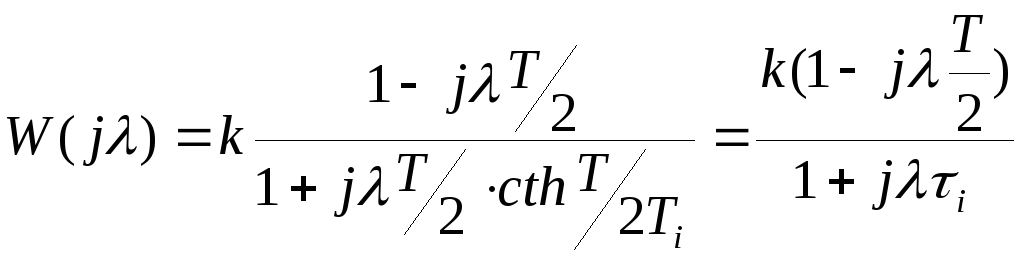так как 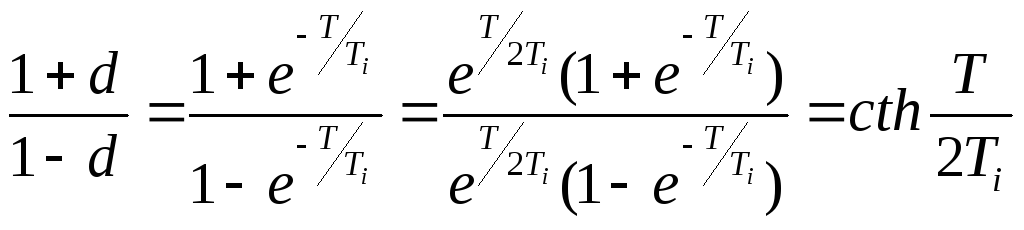. (1)

Исследуем это выражение :

1. Пусть период дискретности [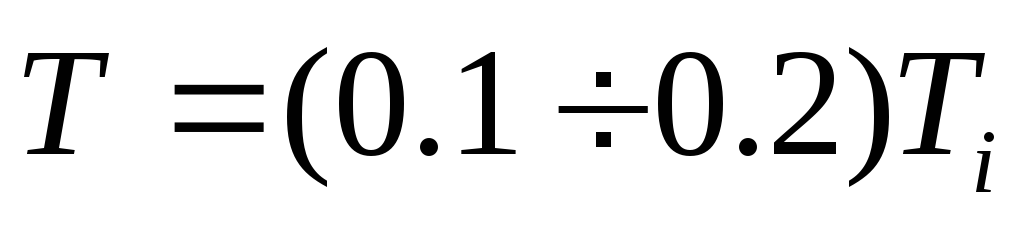] и определим :

, это видно из выражения (1), отсюда , при этих соотношениях .

- неминимально - фазовый множитель.

2. Пусть , тогда , .

.

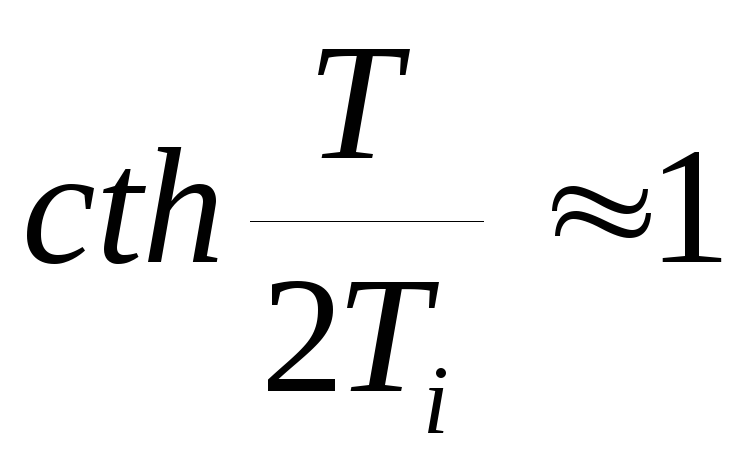Построим частотные характеристики:

1. 2.