Практическое занятие №10

Тема: «Анализ устойчивости микропроцессорных САУ»

Литература

1. Лукас В.А. Теория управления техническими системами.-Екатеринбург: Изд-во УГГУ,2005.

2. Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория базовых знаний,

2002.

.

Пример содержания отчёта

Система автоматического регулирования частоты вращения ротора газотурбинного двигателя

Функциональная схема системы

Напряжение Количество поступающего топлива

МикроЭВМ Объект управления

Дозирующий эл-т Одновальный Скорость

+ _- W_M(z) ЦАП расхода топлива газотурбинный вращения

двигатель ротора

ГТД

Цифровой код ЦД

Структурная схема системы

Дискретная часть системы Непрерывная часть системы

ЦАП

u[n] E[n] y_m[n] y_цап[n] k_цап·y_цап[n] y_цап(t) y_дэ(t) ω_p(t)

W_M(z) ┴ k_цап W_э(p) W_им(p) W_д(p)

Вход разом. y_цд[n] y_цд(t)

размыкание цепи сист. k_цд

ос. Выход разом.

цепи сист. АЦП

Требуется определить дискретную передаточную функцию нескорректированной разомкнутой системы.

Примем W(z)=1. Передаточные коэффициенты цифрового датчика и ЦАП отнесем к непрерывной части системы и обозначим k=k_цдk_дk_цап. Передаточная функция приведенной непрерывной части системы имеет вид

W_пнч(р)=k_цапW_э(p)W_им(p)W_д(p)k_цд,

где

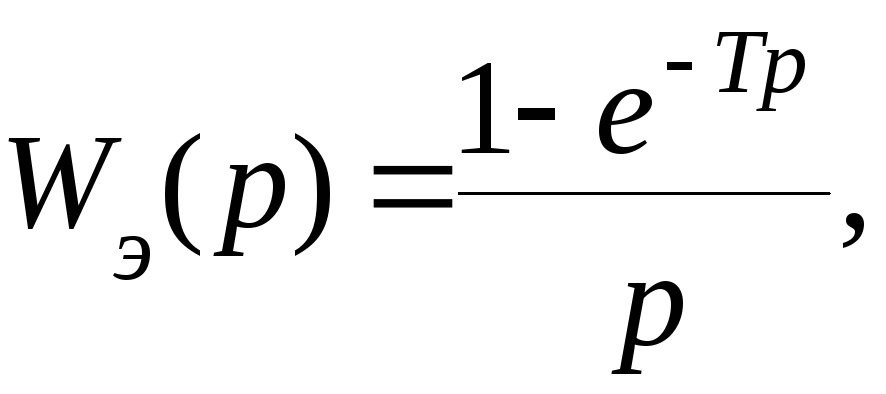
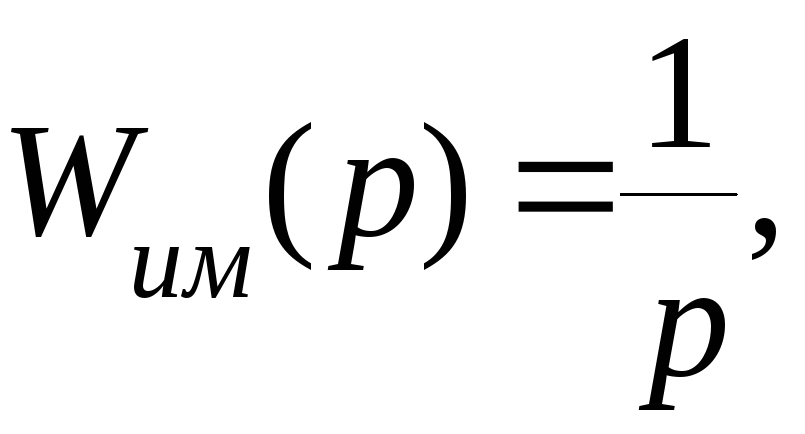
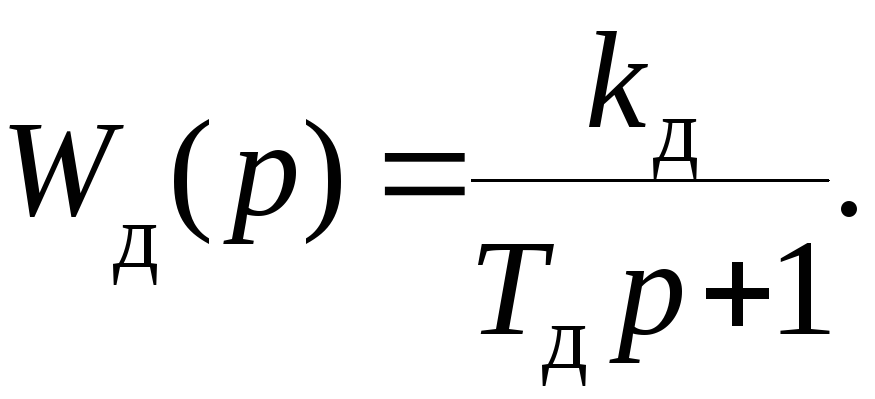
Тогда где Т – такт квантования сигналов.

Разложим выражение в скобках на простые дроби:

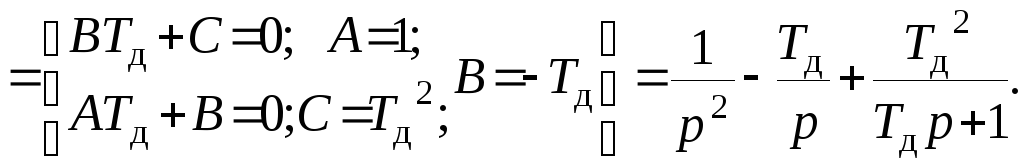
Используя таблицу Z–преобразований, получим Z–изображения слагаемых этого выражения:

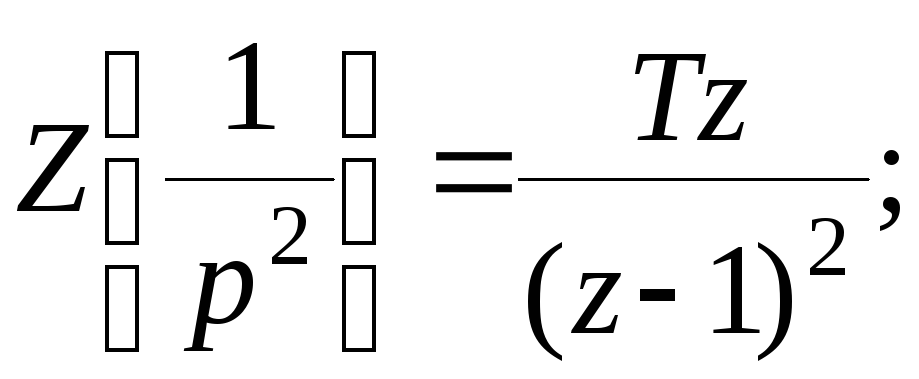
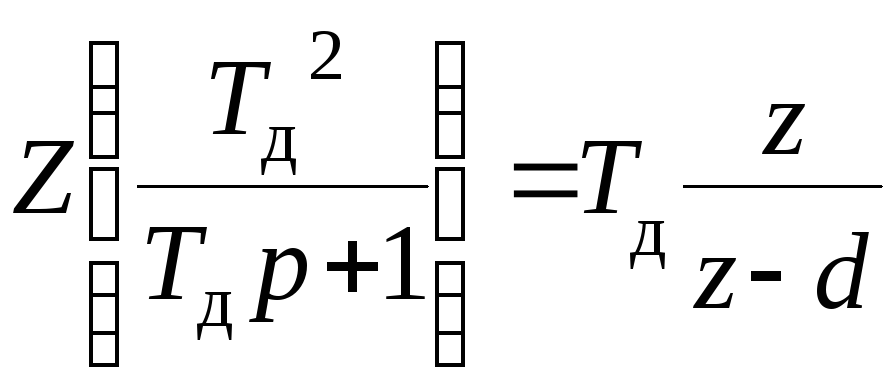, где d=.

Используя эти преобразования получим:

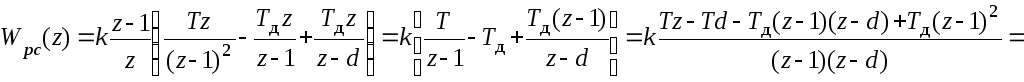
где b₁=T-T_д(1-d); b₀=T_д (1-d)-T_д.

При k=1, T_д=1c, T=0,027c будем иметь

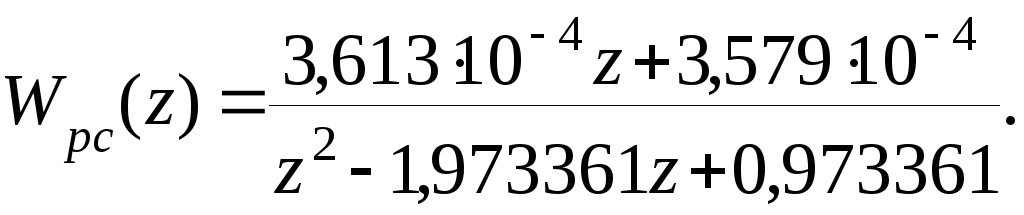
Получим псевдочастотную передаточную функцию путем подстановки 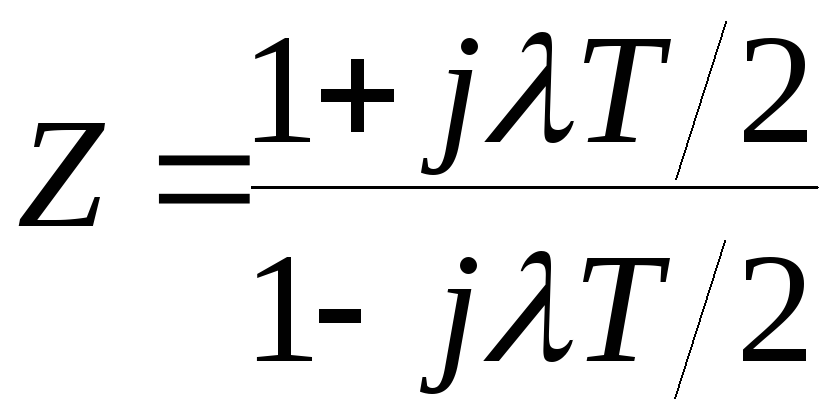в W_pc(z):

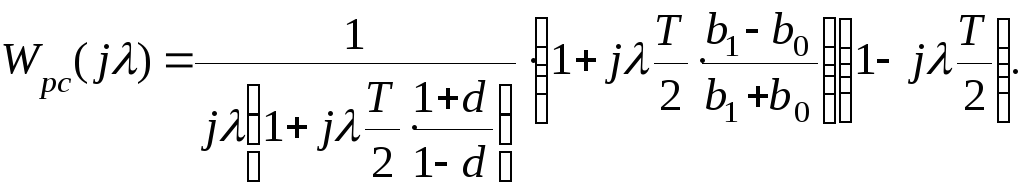
Введя обозначения: , , перепишем последнее выражение в более компактной форме:

Построим асимптотическую логарифмическую амплитудную L(λ) и фазовую θ(λ) частотные характеристики:

L, θ, град

дБ

-20 ΔL-малое число

λ=1 10 λ=2/T 10² 10³ 10⁴ 4,195 10⁵ lgλ

74,07 λ,c^-1

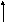λ=1/T₁^* λ=1/τ^*

-40

-90⁰

-20

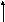
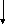
Δθ - малое

-180⁰ число

-270⁰

Система близка к границе устойчивости.

Определим дискретную передаточную функцию замкнутой системы:

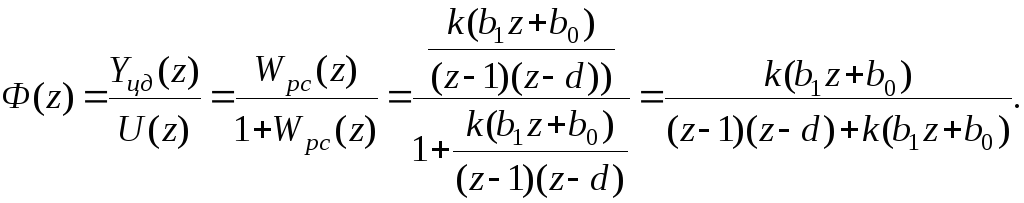
Перейдем к -преобразованию, сделав замену :

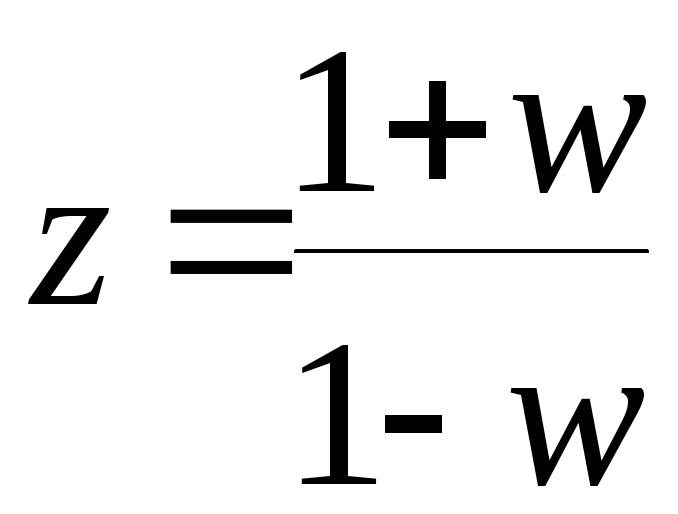Обозначив a₀=2(1+d)-k(b₁-b₀)=2(1+0,973361)-(3,613·10^-4-3,579·10^-4)=3,9467186;

a₁=2(1-kb₀-d)=2(1-3,579·10^-4-0,973361)=0,0525622;

a₂=k(b₀+b₁)= 3,613·10^-4+3,579·10^-4=0,0007192,

получим характеристическое уравнение замкнутой системы:

a₀w²+a₁w+a₂=0.

Согласно критерию Гурвица система устойчива (а₀>0,a₁>0,a₂>0), a₂ – малое значение. Система у границы устойчивости.

Оценим устойчивость системы по модулю корней характеристического уравнения дискретной передаточной функции замкнутой системы:

z²-1,973361z+0,973361=0,

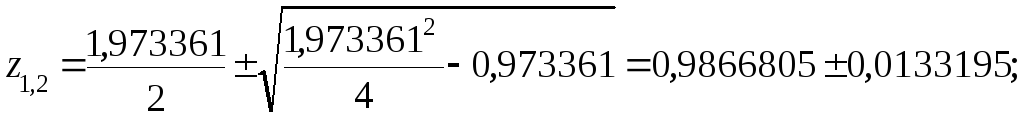
z₁=1, z₂=0,973361.

Система на границе устойчивости.