Курсач мой / курсач мой

Федеральное агентство по образованию Российской Федерации

Пермский государственный технический университет

Кафедра «Динамика и прочность машин»

Курсовая работа по аналитической динамике и теории колебаний

«Расчет частоты колебаний вала

с сосредоточенными массами»

Выполнила:

ст. гр. ДПМ-03

Ивукова Л.А. (вариант 7)

Проверила:

Мельникова Т.Е.

Пермь 2007

Цель работы: Изучить приближенный метод расчета частоты колебаний вала с сосредоточенными массами – метод последовательных приближений; вычислить первую частоту колебаний вала и сравнить ее с частотой, найденной другим приближенным методом.

A m₁ m₂ m₃ m₄ B

50 см 40 см 135 см 85 см 40 см

L=350 см

l. Метод последовательных приближений.

1.Размеры вала:

2.Массы сосредоточенных грузов:

3.Задаем приближенную форму колебаний U_i⁽⁰⁾ (нулевое приближение):

4.Принимаем частоту колебаний:

5. Определяем силы инерции при амплитудных отклонениях системы:

(1)

6.Дифференциальное уравнение изогнутой оси вала имеет вид:

, (2)

где E – модуль упругости (для стали);

I_z(x) – осевой момент инерции поперечного сечения вала ;

u(x) – линейное перемещение центров тяжести поперечных сечений;

M(x) – изгибающий момент в сечении.

7.Найдем реакцию в левой опоре из условия:

(3)

7.Составляем уравнение момента:

Интегрируем его дважды и получаем уравнение прогибов:

(4)

Константы определяем из граничных условий:

(5)

8.Определяем прогибы сечений вала, к которым приложены силы:

9.Определяем приближенное значение частоты собственных колебаний:

10.Прогибы первого приближения являются исходными для второго. По этим прогибам при частоте p⁽¹⁾ найдем силы инерции:

11.Определяем прогибы и частоту во втором приближении:

Полученная во втором приближении частота отличается от частоты, полученной в первом – на 4,5%.

13. Определим прогибы и частоты в третьем, четвертом и пятом приближениях.

Погрешности: для третьего приближения 0,41%, для четвертого приближения 0,44%, а для пятого приближения 0,001%.

ll. Метод Донкерлея.

Приближенная формула Донкерлея имеет вид:

(6)

где δ_ii – податливость балки при приложении силы в точке закрепления массы m_i.

Податливость балки находится как интеграл Мора: (7)

Учитывая, что перемножаются одинаковые эпюры, то можно использовать формулу сопромата: (8)

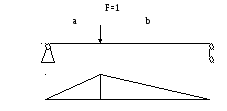
Получаем значения податливостей:

Вычисляем значение частоты:

Формула Донкерлея всегда дает заниженное значение частоты.

Эта частота отличается от частоты, полученной методом последовательных приближений на 9,7%.

Список литературы

1. Бидерман В.А. Теория механических колебаний. М.: Высшая школа, 1980.

408с.

2. Сопротивление материалов: Учеб. для вузов / Под ред. Г. С. Писаренко. Киев: Вища школа, 1979. 696 с.

3. Шевелев Н.А., Мельникова Т.Е. Исследование динамики механических систем: Учеб. пособие / Перм. гос. техн. ун.-т. Пермь, 2007. 50 с.

6