
ЛР №1 / Лабораторная работа №1 / Лабораторная работа №1
.pdf6
1.Применение первичных и избыточных комбинаторных кодов
втелекоммуникационных системах
Вданной главе исследуются первичные (неизбыточные) и избыточные (комбинаторные) коды, в частности, коды на некоторые сочетания (с общей проверкой на четность или нечетность), коды с постоянным весом, коды Бергера. Также проводится анализ комбинаторных и декомбинаторных узлов в трактах передачи дискретных сообщений, реализующих операции кодирования и декодирования исследуемых типов кодов.
1.1.Общие сведения из теории
1.1.1. Первичные (неизбыточные) двоичные коды
Полное множество всех возможных n-разрядных комбинаций указанного класса двоичных кодов
|
|
n n |
|
n |
|
|
n! |
|
|
|||
M |
0 |
= 2n = ∑ |
|
, |
|
|
=Ci |
= |
. |
(1.1) |
||
|
||||||||||||
|
|
|
|
|
|
n |
|
i!(n −i)! |
|
|||
|
|
i=0 i |
|
i |
|
|
|
|||||
Поэтому код, составленный из всех кодовых комбинаций, называют кодом на все возможные сочетания. Следовательно, количество рабочих комбинаций кода Mр (используемых для первичного кодирования сообщений) равно количеству всех комбинаций: Mр = M0.
1.1.2. Комбинаторные избыточные коды
Комбинаторные коды на некоторые сочетания (четные или нечетные)
Комбинации данного кода отбираются из всех возможных сочетаний неизбыточного кода по принципу четности или нечетности веса кодовых комбинаций. Число рабочих комбинаций кода на некоторые сочетания
M р = 2n−1 . |
(1.2) |
Минимальное кодовое расстояние dmin = 2, поэтому r = 1 (dmin – 1). Данный код обнаруживает всевозможные ошибки нечетной кратности, так как именно они нарушают заданную четность (или нечетность) веса. В то же время данный код не обнаруживает ошибки четной кратности, в частности двукратные ошибки.
Проведем оценку избыточности:
|
|
|
|
|
7 |
|
|
|
|
|
|
|
||
|
|
R |
= |
M 0 − M р |
= 2n −2n−1 |
= 0,5, |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
I |
M0 |
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
RII = |
n −m |
|
n −[log2 M р] |
|
n −log2 |
2n−1 |
n −(n −1) |
|
1 |
. (1.3) |
||||
|
= |
|
|
|
|
= |
|
|
= |
|
= |
|
||
n |
|
n |
|
|
n |
|
n |
n |
||||||
|
|
|
|
|
|
|
|
|
|
|||||
I способ формирования: выбор из всех возможных кодовых комбинаций только тех, которые удовлетворяют требованию по четности (нечетности) веса. Количество таких комбинаций – половина от полного множества.
II способ формирования: к кодовой комбинации неизбыточного кода добавляется один дополнительный символ, который и формирует необходимую четность (нечетность) кодовых комбинаций. Он образуется за счет суммирования по модулю два всех символов неизбыточного кода и, если необходимо придать кодовой комбинации нечетный вес, инверсии полученной суммы.
Пример 1.1. Пусть n = 4, тогда M = 24–1 = 8. Техника построения разделимого кода, т.е. кода с явно выраженными информационными (m) и избыточными (k) символами: выписываем все возможные кодовые комбинации 3-разрядного двоичного кода, далее для кода на четные (нечетные) сочетания приписываем 4-й разряд, дополняющий вес кодового слова до четного (нечетного):
m = 3 |
Ч |
Н |
|
|
|
000 |
0 |
1 |
001 |
1 |
0 |
010 |
1 |
0 |
011 |
0 |
1 |
100 |
1 |
0 |
101 |
0 |
1 |
110 |
0 |
1 |
111 |
1 |
0 |
Отметим, что код на четные (нечетные) сочетания широко применяется для обнаружения ошибок при передаче информации по каналам связи, по внутриблочным магистралям, при межузловом обмене. Замечательным свойством разделимого кода на некоторые четные сочетания является его принадлежность к различным классам кодов: комбинаторным, алгебраическим, арифметическим.
8
Двоичные коды с постоянным весом
Код на одно сочетание называется еще кодом с постоянным весом, так как из всех возможных сочетаний неизбыточного кода отбираются только кодовые комбинации одинакового веса (w), а их и образуют коды на одно сочетание. Тогда число рабочих комбинаций такого кода
M = Ci |
n |
, |
(1.4) |
= |
|||
n |
i |
|
|
где i = w.
Для анализируемого кода dmin = 2, r = 1.
Данный код является неразделимым кодом, обнаруживающим ошибки произвольной кратности, нарушающие постоянство веса. В частности, обнаруживаются все возможные однонаправленные ошибки четной кратности, т.е. ошибки типа 0 → 1 или 1 → 0 в пределах одной кодовой комбинации. Симметричные ошибки четной кратности (два и более) не обнаруживаются, так как не нарушают постоянства веса. При симметричных ошибках в пределах одной кодовой комбинации допускаются одновременно переходы 0 → 1 и 1 → 0. Отметим, что асимметричные ошибки, т.е. ошибки только одного знака, являются частным случаем однонаправленных ошибок. Код с постоянным весом оптимален в полностью асимметричных каналах, т.е. не существует кода с той же обнаруживающей способностью, имеющего меньшую избыточность.
Пример 1.2. Построим следующий код с постоянным весом w = 2:
M = 42 = 6 , dmin = 2, r = 1.
Кодовая таблица:
1100
0110
0011
1001
1010
0101
Оценим избыточность кода: |
|
|
|
|
|||||
RI = |
32 − 6 |
= 0,813; |
RII = |
n −[log M ] |
= |
4 − 3 |
= 0,25. |
||
32 |
|
n |
4 |
|
|||||
|
|
|
|
|
|
|
|||
Из этого примера видно, насколько грубее оценка RII. Кроме того, из приведенных выше рассуждений становится понятней, на обнаружение каких дополнительных (по сравнению с кодом на некоторые сочетания) ошибок расходуется большая избыточность кода с постоянным весом.

9
Одним из основных недостатков данного кода является то, что он неразделимый и нелинейный. Поэтому область его применения достаточно ограниченна. В частности, он применяется для кодирования внутренних состояний цифровых автоматов.
Код Бергера
Существует разделимый квазиоптимальный код для полностью асимметричных каналов, называемый кодом Бергера. Структура кодовых слов его показана на рис. 1.1.
k =[log2 (m +1)]
Рис. 1.1. Структура кодовых слов кода Бергера
Процедура кодирования такова. На первых m позициях размещаются информационные символы, на последних k позициях – избыточные сим-
волы, причем k = [log2 (m + 1)].
Избыточные символы представляют собой инверсию от записи в двоичном позиционном коде текущего веса информационного m-раз- рядного вектора.
Пример 1.3. Пусть m = 5, тогда k = [log2 (m + 1)] = 3.
Пусть кодируемое сообщение является 01011, тогда вектор кода Бергера имеет вид 01011 100.
Код Бергера так же, как и код с постоянным весом, обнаруживает асимметричные ошибки любой кратности (в пределах кодового слова), но имеет большую избыточность.
Пример 1.4. Код с постоянным весом M = |
9 |
=126 имеет избыточ- |
|
4 |
|
ность RI = 512 −126 = 0,75. Код Бергера, передающий то же множество
512
сообщений, имеет m = 7 и k = 3, т.е. его избыточность
= 1024 −128 =
RI 0,87. 1024
Способность кода Бергера обнаруживать асимметричные (однонаправленные) ошибки обусловлена следующим.
Пусть произошли ошибки одного знака, например 0 → 1, в информационной и избыточной частях кодового вектора. В информационных символах эти ошибки увеличили вес информационного вектора, а в избыточных символах вес двоичного слова уменьшился в результате операции

10
инвертирования, произведенной в декодере. Поэтому маскирование ошибки не произойдет и она будет обнаружена.
Пример 1.5. Пусть исходный кодовый вектор V = 01011 100, искаженный вектор V ′ = 11111 101. После декодирования, в результате инвертирования избыточной части получим вектор V ′′ = 11111 010.
Таким образом, асимметричные ошибки увеличивают (уменьшают) текущий вес информационного кодового слова, одновременно уменьшают (увеличивают) вес избыточного слова. Поэтому любая асимметричная (однонаправленная) ошибка будет обнаружена.
Выше были рассмотрены наиболее популярные комбинаторные коды. Но список этих кодов значительно шире. Кроме того, не рассматривались низкоскоростные коды с подстановками, у которых в качестве внешних и внутренних кодов используются комбинаторные коды. Для кодов с подстановками кодовое расстояние равно произведению кодовых расстояний внешнего и внутреннего кодов. Таким образом, можно сравнительно просто построить коды, исправляющие ошибки, которые могут найти применение в трактах телеуправления (ТУ), телесигнализации (ТС), телерегулирования (ТР). Это обусловлено малым объемом передаваемых сообщений в указанных трактах и сравнительно низкими требованиями к скорости передачи информации, т.е. допустима большая избыточность.
1.1.3.Проектирование комбинаторных узлов неизбыточных
иизбыточных кодов
Назначение комбинаторных устройств (узлов) – формирование одноступенных и многоступенных первичных (неизбыточных) и избыточных (комбинаторных) кодов.
Одноступенные комбинаторные узлы (КМУ)
Основой КМУ является комбинатор (КМ). Комбинатор – это логический (l, f)-многополюсник (комбинационная схема), имеющий l входов и f выходов и реализованный из дизъюнкторов.
Будем различать два типа КМУ в зависимости от способа включения КМ в состав комбинаторного устройства, влияющего на технические характеристики КМУ. В частности, способ включения определяет структуру КМУ и время формирования кодовых слов.
Для первого тип КМУ характерно включение КМ между ключами управления в тракте ТУ (блок-контакты объектов ТС) и буферным регистром. Комбинатор представляет собой логический (М, n)-многополюсник, состоящий из n многовходовых дизъюнкторов, где М – число кодируемых
11
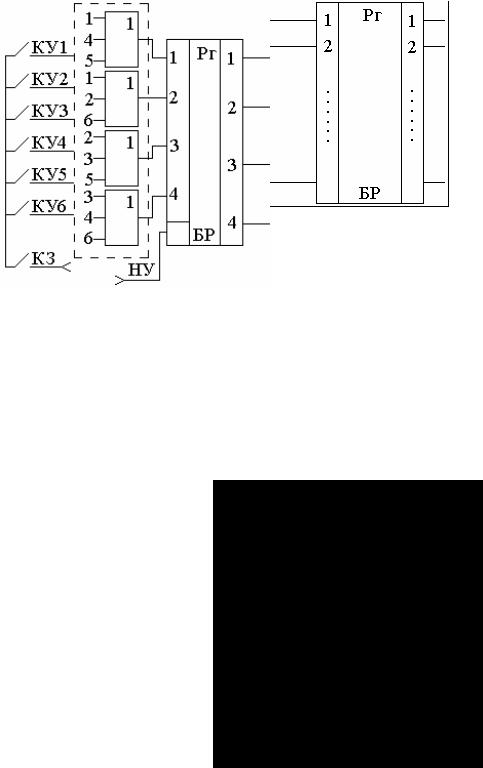
сообщений, n – длина кодовых слов избыточных (комбинаторных) или неизбыточных кодов, формируемых за один такт. На рис. 1.2 представлена обобщенная функциональная схема КМУ первого типа.
Рис. 1.2. Обобщенная функциональная схема КМУ первого типа
Пример 1.6. Построить КМУ первого типа, формирующий код с по-
стоянным весом M = 42 . Согласно изложенному выше комбинатор в дан-
ном примере – это (6, 4)-многополюсник, состоящий из 4 трехвходовых дизъюнкторов.
На рис. 1.3 приведены кодовая таблица и функциональная схема КМУ первого типа.
Следует отметить, что каждый из 4 дизъюнкторов реализует один из столбцов кодовой таблицы, а единицы соответствующего столбца определяют связь входов дизъюнкторов и ключей управления.
1 – 1100
2 – 0110
3 – 0011
4 – 1001
5 – 1010
6 – 0101
а
б
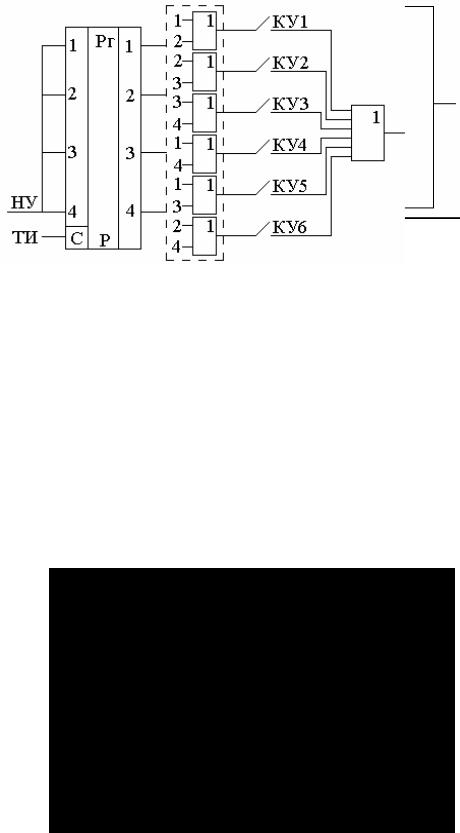
Рис. 1.3. Кодовая таблица (а) и функциональная схема КМУ первого типа (б)
12
Рис. 1.4. Обобщенная функциональная схема КМУ второго типа
Для второго типа КМУ характерно включение КМ между распределителем (формирователь временных каналов) и ключами управления в тракте ТУ (блок-контактами объектов ТС в тракте ТС). Комбинатор представляет собой логический (n, М)-многополюсник, состоящий из М многовходовых дизъюнкторов. КМУ этого типа формирует кодовые слова за n тактов. На рис. 1.4 показана обобщенная функциональная схема КМУ второго типа.
Пример 1.7. Построить КМУ второго типа, формирующий код с по-
= 4
стоянным весом M 2 . Комбинатор в составе КМУ представляет собой
(4, 6)-многополюсник, состоящий из шести двухвходовых дизъюнкторов (рис. 1.5). Кодовая комбинация формируется за 4 такта.
Рис. 1.5. Функциональная схема КМУ второго типа,
формирующего код M = 42
13
Отметим, что по основным техническим характеристикам КМУ первого и второго типов являются инверсными.
1.1.4.Проектирование декомбинаторных узлов неизбыточных
иизбыточных кодов
Назначение декомбинаторных устройств (узлов) – отображение (декомбинирование) дискретного множества кодовых слов (комбинаций) неизбыточных (первичных) или избыточных (комбинаторных) одноступенных и многоступенных кодов на дискретное множество сообщений.
Рассмотрим краткую классификацию декомбинаторных узлов (ДКМУ):
1.По числу ступеней декомбинируемого кода:
–одноступенные;
–многоступенные.
2.По структуре декомбинатора (ДКМ):
–матричные;
–пирамидальные;
–координатные.
Наибольшее распространение получили матричные декомбинаторы, поэтому в данном подразделе в основном рассматриваются матричные ДКМУ.
3. По применению декомбинаторов в составе других функциональных узлов:
–декомбинаторный узел передаваемых сообщений;
–в составе распределительных узлов;
–в составе декодера (кодера).
Внастоящем подразделе рассматриваются только декомбинаторные узлы передаваемых сообщений (ДКМУ).
Одноступенные матричные ДКМУ
Основой матричного ДКМУ является матричный декомбинатор. Матричный ДКМ – это ((2n + 1), М)-многополюсник (комбинационная схема), состоящий из М (n + 1)-входовых конъюнкторов, где n – длина декомбинируемого кода, М – множество передаваемых сообщений. Обязательным элементом ДКМУ является буферный регистр (БР) на входе ДКМ, обеспечивающий хранение кодовой комбинации, поступившей из канала связи, и синхронную подачу ее на вход ДКМ.
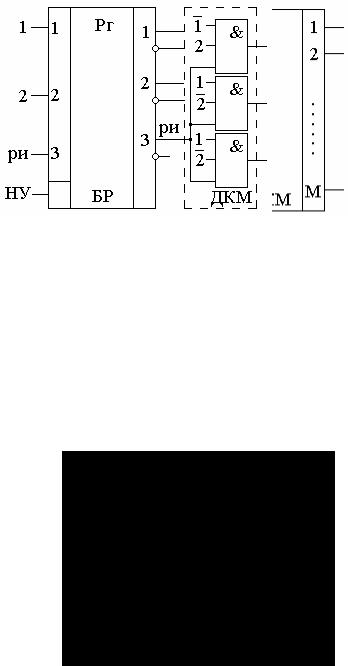
Обобщенная функциональная схема матричного ДКМУ приведена на рис. 1.6.
|
|
14 |
|
|
|
|
|
S |
|
X/Y |
|
S |
|
|
|
nS |
|
|
|
n |
n |
n |
|
n |
n |
||
R |
|||
|
|
|
Рис. 1.6. Обобщенная функциональная схема одноступенного матричного ДКМУ
С выхода ДКМУ декомбинированное сообщение поступает в индивидуальные узлы управления – ИУУ (тракт ТУ), индивидуальные узлы сигнализации – ИУС (тракт ТС), узлы коммутации датчиков телеизмерения по запросам оператора (тракт ТИ). (n + 1)-й входы БР и ДКМ связаны с сигналом разрешения исполнения (РИ), обеспечивающим синхронную подачу входного сигнала на ДКМ, что позволяет избежать рисков на выходе ДКМУ. Рассмотрим ряд примеров построения одноступенных матричных ДКМУ неизбыточных и комбинаторных кодов.
Рис. 1.7. Функциональная схема неизбыточного кода М = 22
Пример 1.8. Построить ДКМУ двоичного неизбыточного кода М = 2n. Пусть n = 2, тогда матричный ДКМ – это (5,4)-многополюсник, состоящий из М = 4 трехвходовых конъюнкторов. Функциональная схема ДКМУ приведена на рис. 1.7.
Пример 1.9. Построить ДКМУ двоичного кода с постоянным весом
M = 23 , для которого dmin = 2. В данном случае матричное ДКМУ – это
15
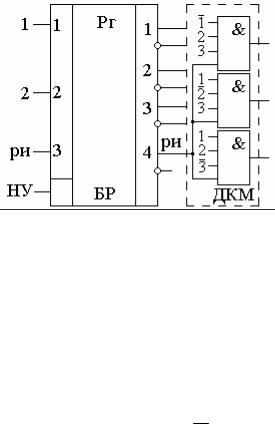
(7, 3)-многополюсник, состоящий из М = 3 четырехвходовых конъюнкторов. Функциональная схема ДКМУ приведена на рис. 1.8.
Рис. 1.8. Функциональная схема ДКМУ кода с постоянным весом M = 23
Следует обратить внимание на то, как реализуется в данном случае обнаруживающая способность избыточного кода. Каждый из М = 3 конъюнкторов реализует одну из М сигнальных зон, включающих в себя только рабочую комбинацию кода. В том случае, когда возникает обнаруживаемая ошибка, приводящая к изменению веса, срабатывает дополнительная комбинационная схема, реализующая булеву функцию:
M |
|
ε = PИ∏xi |
(1.5) |
i=1
где хi – значение булевой функции на выходе i-го конъюнктора матричного ДКМ.
При ε = 1 происходит стирание кодовой комбинации, записанной в БР ДКМУ.
Возможны и другие варианты реализации обнаруживающей способности кода с постоянным весом, например подсчет веса кодовой комбинации на выходе ПРС с помощью дополнительного двоичного счетчика.
1.2.Порядок выполнения лабораторной работы
1.2.1.Выполнение расчетной части лабораторной работы
1.Выбрать вариант задания на лабораторную работу. Для этого сначала для своего номера в списке группы необходимо определить тип кода, который будет использован в работе (по табл. 1.1). В ней используются следующие условные обозначения: n – общая длина кодовой комбинации, m – длина информационной части кодовой комбинации, W – вес рабочей кодовой комбинации.
