Контр раб 9 вар 1курс

Контрольная работа №1

Элементы векторной алгебры, аналитической геометрии и линейной алгебры

1.1.59. Найти объем параллелепипеда, построенной на векторах:

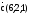, . Сделать чертеж.

Решение

(ед³)

2.1.19. Даны уравнения двух медиан треугольника х-2у+1=0 и у-1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж.

Решение.

Пусть т.В имеет координаты (х₁;у₁), т.к. точка К по условию есть середина отрезка АВ, то ее координаты равны и удовлетворяют уравнению х-2у+1=0, то

. Кроме того координаты точки В(х₁;у₁) удовлетворяют уравнению у-1=0, получаем систему линейных алгебраических уравнений

, т.В(5;1)

Аналогично найдем координаты точки С(х₂;у₂). Пусть N – середина отрезка АС, тогда координаты точки находятся по формулам , т.С(-3,-1)

Уравнение АВ: или или х+2у-7=0 (АВ)

Уравнение ВС: или 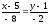или х-4у-1=0 (ВС)

Уравнение АС: или или х-у+2=0 (АС)

А

В

С

К

N

Ответ: х-у+2=0 (АС), х-4у-1=0 (ВС), х+2у-7=0 (АВ)

2.2.49 Составить уравнение плоскости, проходящей через прямые:

и 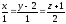. Сделать схематический чертеж.

Найдем на первой прямой две точки, на второй одну точку и проведем через них плоскость.

Пусть t=0, тогда получим точку М₁(-1,0,1), пусть t=1, тогда получим точку М₂(0,1,3).

Пусть t=0, тогда получим точку М₃(0,2,-1).

Оно представляется уравнением:

– искомое уравнение плоскости.

3.1.39. Приведите к каноническому виду уравнения линий второго порядка. Установите тип этих линий и их расположение. Сделайте схематический чертеж.

Решение.

Преобразуем уравнение линии второго порядка

Получаем уравнение 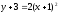- парабола, направленная вдоль оси Оy–получена смещением по ОХ на -1 ед. и вдоль Оу на -3 ед.

у=2х²

3.2.9 Дана (4Х4) –система линейных уравнений. Доказать ее совместность и решить методом Гаусса (методом исключения неизвестных). Сделать проверку

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:

=[ умножаем четвертую строчку на -1 и складываем с первой, умножаем вторую на -2 и складываем с первой, умножаем третью на -2 и складываем с первой]=

= [умножаем вторую строку на -3, третью на 5 и складываем их]= =[умножаем третью строку на 5, четвертую на 12 и складываем их]=

Система совместна, значит имеет единственное решение, находим корни, решая систему

Находим решения

х₁=-1, х₂=3, х₃=2, х₄=1

Сделаем проверку, подставив в исходную систему уравнений

или

Получаем верные равенства.