Контр раб 8вар 1 курс

Контрольная работа №1

Элементы векторной алгебры, аналитической геометрии и линейной алгебры

Вариант 8

1.1.58. Найти площадь параллелограмма, построенного на векторах: (7;0;3); (-4;1;-2). Сделать чертеж.

Решение

Площадь параллелограмма, построенного на векторах 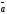(7;0;3); 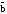(-4;1;-2)

(ед. кв.)

Ответ: (ед. кв.)

2.1.18 Даны уравнения двух высот треугольника х+у=4 и у=2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника. Сделать чертеж.

Решение.

Точка A(0, 2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям: х+у=4 и у=2х. Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника B и C.

Назовем их CD и BE, CDAB, BEAC. Пусть высота CD имеет уравнение x+y-4=0, а уравнение высоты BE: 2х-у=0.

Прямая, проходящая через точку M(x₁,y₁) и перпендикулярная к прямой Ax+By+C=0, представляется уравнением A(y-y₁) – B(x-x₁) = 0.

Получим уравнение прямой АС: 2(у-2)+1(х-0)=0 или х+2у-4=0 искомое уравнение АС.

Уравнение прямой AB найдем, как уравнение прямой, проходящей через точку A(2, 0) перпендикулярно CD: х+у-4=0. Оно имеет вид

(у-2)-1(х-0)=0 или –х+у–2=0 искомое уравнение АВ.

Найдем координату точки C, как точку пересечения прямых СD и АC решая систему уравнений:

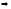C(4;0)

Найдем координату точки B, как точку пересечения прямых ВЕ и АВ решая систему уравнений:

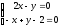
В(2;4)

Уравнение стороны BC: или

-4x-2y+16=0

Таким образом, уравнения всех трех сторон треугольника найдены.

А

В

С

D

E

Ответ: АВ: –х+у–2=0; ВС: -4x-2y+16=0; АС: х+2у-4=0

2.2.48. Составить уравнение плоскости, проходящей через т.А(3;2;-1) и прямую . Сделать схематический чертеж.

Решение.

Преобразуем уравнение плоскости к параметрическому виду:

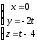
Найдем две любые точки прямой. При t=1 т.В(0;-2;-3), при t=2 т.С(0;-4;-2)

Пусть имеется три точки А(x₁,y₁,z₁), В(x₂,y₂,z₂), Сx₃,y₃,z₃), тогда уравнение плоскости, проходящее через три точки определяется формулой:

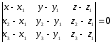
Найдем уравнение плоскости АВС:

Ответ: -8x+3y+6z+24=0

3.1.38. Приведите к каноническому виду уравнения линий второго порядка. Установите тип этих линий и их расположение. Сделайте схематический чертеж.

Решение.

А=8, В=2, С=5, D=8, Е=2

>0 эллиптический тип

Сделаем замену

А=8, В=2, С=5

D=9-4·2·(-2)=25

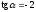· или

Будем рассматривать, тогда

Получили уравнение эллипса центр которого смещен в точку (1;0), и повернутого на угол

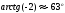
3.2.8. Дана (4×4) система линейных уравнений. Доказать ее совместность и решить методом Гаусса (методом исключения неизвестных). Сделать проверку.

Решение.

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду.

=[ Поменяем местами первую и третью строчки]=

=[умножим первую строку на -2 и сложим со второй, умножим первую строку на -3 и сложим с третьей и четвертой]=

=[умножим вторую строку на -7 и сложим с третьей, умножим вторую строку на -1 и сложим с четвертой]=

Решаем систему уравнений

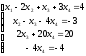
Получаем х₁=3 х₂=1 х₃=0 х₄=1

Сделаем проверку, подставляем решения в исходную систему

Ответ: х₁=3 х₂=1 х₃=0 х₄=1.