Контр раб 7 вар 1курс

Контрольная работа №1

Элементы векторной алгебры, аналитической геометрии и линейной алгебры

1.1.57. Найти объем параллелепипеда, построенной на векторах:

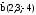
, . Сделать чертеж.

Решение

(ед³)

Ответ: 159ед³

2.1.17 Даны две вершины А(2; –2) и В(3; –1) и точка Р(1; 0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.

Решение.

Найдем координаты точки М

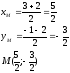
Уравнение стороны АВ: или

Тогда угловой коэффициент

_{Уравнение высоты} CD будем искать в виде:

_{В силу перпендикулярности:}

_Т.к. С лежит на высоте CD, то

_{Искомое уравнение: у=-х+1.}

2.2.47 Составить уравнение плоскости, проходящей через прямыеи .Сделать схематический чертеж.

Найдем на первой прямой две точки.

Пусть t=0, тогда получим точку М₁(0,1,-1), пусть t=1, тогда получим точку М₂(2,2,-1).

Найдем на второйпрямой одну точку.

Пусть t=0, тогда получим точкуА(2,-2,0).

Плоскость представляется уравнением:

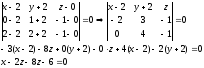
– искомое уравнение плоскости.

3.3.37. Приведите к каноническому виду уравнения линий

второго порядка. Установите тип этих линий и их расположение. Сделайте схематический чертеж.

Решение.

, ,

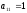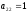
или

Будем рассматривать, тогда

Получили уравнение гиперболы с вершиной в точке (;-).

3.2.7. Дана система линейных уравнений. Доказать ее совместность и решить методом Гаусса (методом исключения неизвестных). Сделать проверку.

Решение.

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду.

=[ умножим вторую строку на -2 и сложим с первой, умножим третью строку на -2 и сложим с первой, умножим четвертую строку на -1 и сложим с первой]=

=[умножим вторую строку на -3, третью на 5 и сложим их, умножим вторую строку на 3, четвертую на 5 и сложим их]=

=[ умножим четвертую строку на -4 и сложим с третьей]=

Решаем систему уравнений

Получаем х₁=2 х₂=-2 х₃=1 х₄=-1

Сделаем проверку, подставляем решения в исходную систему

Ответ: х₁=2 х₂=-2 х₃=1 х₄=-1