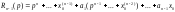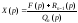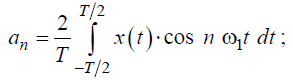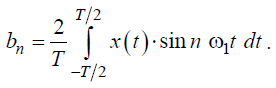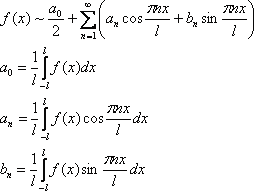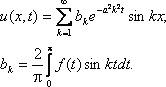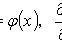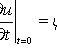Комплексные числа в алгебраической форме
.docx
Комплексным
числом называется выражение вида
Числа
Выражение
Множество
комплексных чисел обозначается
Из
определения следует, что действительные
числа можно рассматривать как частный
случай комплексных, т.е.
Число
|
Каждому
комплексному числу
Величина
Используя
связь декартовых и полярных координат
точки
|
|
Если
обозначить комплексное число
Равенство
Заметим,
что геометрически задание комплексного
числа
Действия над к.ч.
|
Многие из понятий,
введенных для последовательностей
действительных чисел, обобщаются на
последовательности комплексных чисел,
причем с сохранением ряда свойств.
Комплексное число называется
пределом
последовательности комплексных чисел
{zn},
если для любого
В
этом случае пишут
Последовательность {zn} комплексных чисел называется ограниченной, если ограничена последовательность действительных чисел {|zn|} (т. е. если ограничена последовательность абсолютных величин членов данной последовательности). 1°
Предел суммы/разности двух функций
равен сумме/разности их пределов:
2°
Предел произведения двух функций
равен произведению их пределов: 3°
Предел частного двух функций равен
частному их пределов, при условии, что
предел знаменателя не равен нулю: 4°
Константу можно выносить за знак
предела: 5°
Предел степени с натуральным
показателем равен степени предела:
|
|
Основные понятия, связанные с функцией комплексного переменного, находятся так же, как и в действительной области.
Пусть
заданы два множества
Если
каждому значению
Если
записать числа
Задание
функции
|
Производная
функции комплексного переменного в
точке
Здесь
Функция, имеющая производную в точке, называется дифференцируемой в этой точке; функция, дифференцируемая в каждой точке области, называется дифференцируемой в области.
Условия
Коши-Римана,
которые также в некоторых источниках
называются условиями
Даламбера-Эйлера
- соотношения, связывающие вещественную
Для
того чтобы функция
|
|
|
|
|
|
Если
существует
Итак, по определению, криволинейный интеграл II рода
|
|
В теории и практике применения функций комплексного переменного интерес представляют дифференцируемые функции, причем имеющие производные не в отдельных точках, а на множествах — в областях. Такие функции называют аналитическими. Имеют место следующие определения. 1. Функция, дифференцируемая в каждой точке области, называется аналитической в области. 2. Функция, аналитическая в окрестности некоторой точки, называется аналитической в этой точке. 3. Функция называется аналитической на замкнутом множестве если она является аналитической в некоторой области, содержащей это множество 4. Точки, в которых нарушается аналитичность функции, называются её особыми точками. Если функция непрерывна в области и в каждой точке области выполняются условия Коши-Римана, то функция является аналитически в области. Арифметические свойства Если
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Если множество нулей аналитической в односвязной области функции имеет в этой области предельную точку, то функция тождественно равна нулю. Для функции от нескольких действительных переменных аналитичности по каждой из переменных недостаточно для аналитичности функции Логарифмическая функция Имеет вид : z=ew где z, w – комплексные числа. Def: если на некоторой области D существует функция w=f(z) которая является однозначной на этом множестве, тогда существует обратная функция z=φ(w) Прологорифмируя функцию z=ew получим w=ln|r|+iargz, r=sqrt(x^2+y^2) argz- главное значение агрумента
|
Опр: числовым рядом от комплексного переменного называется числовой ряд z1+z2+…+zn=∑zn Опр. Частичной суммой числового ряда называется Sn= z1+z2+…+zn Числовой ряд называется сходящимся если существует предел Sn при n->бесконечность. Примечание. Все признаки обыкновенных числовых рядов остаются справедливыми для рядов с комплексными членами. Степенные ряды. Определение
Ряд,
членами которого являются степенные
функции аргумента x,
называется степенным
рядом:
Часто
рассматривается также ряд, расположенный
по степеням (x−x0),
то есть ряд вида
где x0 − действительное число. Интервал и радиус сходимости
Рассмотрим
функцию
|
|
Опр. Область D называется односвязной, если любой замкнутый контур расположенный в области D можно стянуть в одну точку. Теорема Коши: если функция f(z) аналитическая на односвязной области D, то интегралом от f по любому кусочно-гладкому контуру, принадлежащему D = 0.
Теорема
2: пусть
область D
компелксной плоскости ограничена
положительно ориентированным
кусочно-гладким контуром Г, тогда для
f(z)
аналитической на границе области D
справедливо тождество
Область D в этом случае может быть не односвязной. Теорема 3: пусть область D ограничена внешним контуром Г ориентрованным против часовой стрелки(внутренний контур так же ориентирован) и пусть на границе D задана аналитическая функция f(z) тогда имеет место тождество
|
|
|
Ряд
Лорана —
двусторонний бесконечный степенной
ряд по целым
степеням
Этот ряд является суммой двух рядов:
|
Точка
а Бесконечно
удаленная точка называется изолированной
особой точкой однозначного характера
функции f (z),
если f (z)
регулярна в некоторой окрестности
{R<|z|< имеет в точке =0 изолированную особую точку однозначного характера. В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек. Изолированная особая точка а функции f (z) называется а) устранимой особой точкой, если существует конечный предел
б) полюсом, если
в) существенно особой точкой, если
не существует.
|
|
Лемма. Если функция F(z) регулярна в кольце {z:r<|z–a|<R}, то интеграл
Пусть
z=a
– изолированная особая точка
однозначного характера функции f (z).
Вычетом
функции f (z)
в точке z=a
(а
(
>0 – любое достаточно малое число).
При а=
(R>0 – любое достаточно большое число). Направление интегрирования выбрано так, чтобы внутренность круга осталась слева. Независимость интегралов в последних формулах от и R соответственно следует из леммы.
|
Вычет относительно бесконечно удаленной точки
(f(z)
- аналитическая в области
c-1
- коэффициент при z-1
в разложении f(z)
в ряд Лорана в окрестности точки
|
|
Основная теорема о вычетах. Пусть функция f (z) регулярна всюду в замкнутой области D за исключением конечного числа изолированных особых точек а ( =1, 2, 3,…, n), лежащих внутри области D. Тогда
где Г – граница области D, проходимая в положительном направлении.
|
Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал). Преобразованием Лапласа от функции f(x) (оргигинала) называется функция:
f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа. f(x) и F(p) однозначно определяются друг относительно друга, тоесть если Вы знаете f(x), то всегда можете узнать F(p), и наоборот, если знаете F(p), то всегда можете получить f(x).
|
|
Простейшей
функцией-оригиналом является единичная
функция Хевисайда
Если
В
дальнейшем мы будем писать
1.2.
Функция
Тот
факт, что
Изображение
функций Хевисайда,
|
Теорема
подобия. Если
изображение функции
Пример
1.
Тогда
|
|
Свойство
линейности изображения. Изображение
суммы нескольких функций, умноженных
на постоянные, равно сумме изображений
этих функций, умноженных на соответствующие
постоянные, то есть если
Пример 2. Изображение
функции
1.5.
Теорема смещения. Если
Эта теорема позволяет расширить класс функций, для которых легко находятся оригиналы по данному изображению. Используя
данную теорему, получим изображение
функций
Гиперболическая
функция
Аналогично
можно найти изображение гиперболического
косинуса: т.к.
Зная
изображения
|
Дифференцирование
изображения. Если
Откуда
Применяя
теорему смещения к этому изображению,
получим
На
основании теоремы дифференцирования
изображения можно получить изображения
функций
|
|
Если f(n)(t) - оригинал с показателем роста , и f(t) F(p), то f(n)(t) pnF(p)-pn-1f(0)-pn-2f `(0)-...-pf(n-2)(0)-f(n-1)(0) при Rep. В частности, если f(0) =f `(0) =...=f(n-1)(0)=0, то f(n)(t) pnF(p) (при дифференцировании оригинала изображение умножается на р).
|
Интегрирование
оригинала. Если
Интегрирование
изображений. Если
|
|
Теорема
запаздывания. Если
Замечание.
Теорему
целесообразно использовать при
отыскании изображений функций, которые
на разных участках задаются разными
аналитическими выражениями. При этом
удобно записывать функцию
|
Рассмотрим линейное дифференциальное уравнение
где ak –действительные числа. Требуется найти решение данного дифференциального уравнения, удовлетворяющее начальным условиям x(0)=x0, x`(0)=x`0, …, x(n-1)(0)=x0(n-1) где x0, x`0, …, x0(n-1) – заданные числа. Будем предполагать, что искомая функция x(t), все ее производные, а также функция f (t) являются оригиналами.
Пусть
Перейдем от данного дифференциального уравнения к уравнению в изображениях
Перепишем его так
Находим так называемое операторное решение уравнения
Найдя оригинал x(t) по его изображению X(p) , мы получим тем самым решение задачи Коши для исходного дифференциального уравнения. |
|
|
Ряд Фурье функции x(t) представляется в виде :
где коэффициенты Фурье a0, an и bn определяются формулами
При расчете коэффициентов ряда Фурье необходимо выбрать начальный момент времени t0 периода интегрирования. Как правило, значение t0 выбирают так, чтобы упростить вычисления. Обычно, исходя из этого условия, принимают t0=-Т/2 . Формулы приобретают следующий вид:
|
|
Если функция x(t), описывающая сигнал, является четной, то есть x(t)=x(-t), то коэффициенты an=0, n=0,1,2,…, и в разложении остаются только постоянная и косинусоидальные составляющие:
Если функция x(t), описывающая сигнал, является нечетной, то есть x(t)=-x(t), то коэффициенты an=0, n=0,1,2,…, и в разложении остаются только синусоидальные составляющие:
Получила распространение и другая форма записи тригонометрического ряда Фурье:
где амплитуда An и фаза n-ой гармонической составляющей связаны с коэффициентами an и bn соотношениям:
или
|
Для
произвольного периода разложения
Если
Алгоритм и принципы решения задачи полностью сохраняются, но возрастает техническая сложность вычислений:
|
|
Температуру физического тела в произвольной точке с координатами (x, y, z) в момент времени t можно представить в виде функции:
Составим дифференциальное уравнение:
Выражение
Тогда составленное нами дифференциальное уравнение принимает вид:
и называется уравнением теплопроводности в пространстве. В качестве частных случаев рассматривают:
В
случае рассмотрения уравнения
теплопроводности в стержне искомая
функция u(x,
t)
должна удовлетворять записанному
выше дифференциальному уравнению,
начальному условию
|
В результате решения дифференциального уравнения методом Фурье получим:
|
|
Решение:
где
|
Метод Фурье для уравнения колебаний ограниченной струны
Начальные
условия:
Граничные
условия:
Решение:
где
|
|
|
|

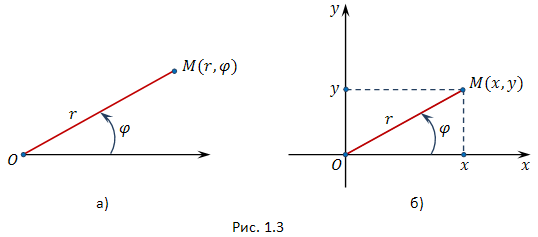
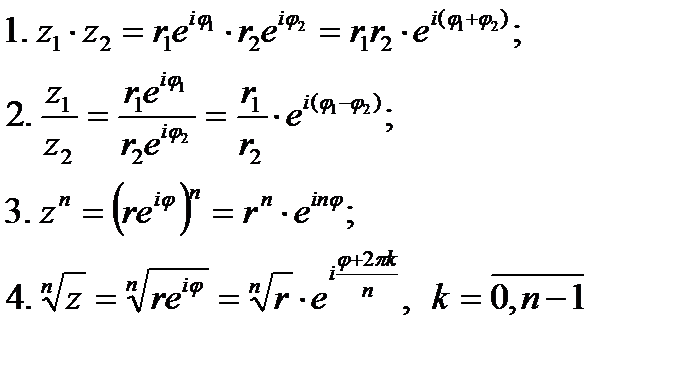


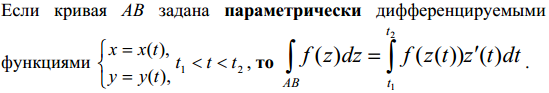

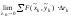 ,
не зависящий ни от способа разбиения
дуги
,
не зависящий ни от способа разбиения
дуги
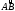 на части, ни от выбора точки
на части, ни от выбора точки
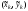 ,
то этот предел называется криволинейным
интегралом II
рода и
обозначается
,
то этот предел называется криволинейным
интегралом II
рода и
обозначается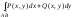 или
или
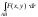 .
.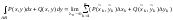 ,
,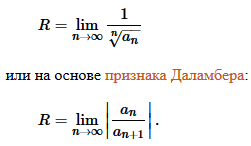
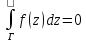
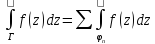


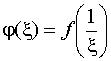
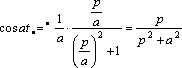 ;
таким образом,
;
таким образом,
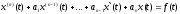
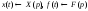 .
По формулам дифференцирования
оригиналов
.
По формулам дифференцирования
оригиналов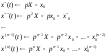
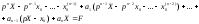
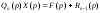 ,
где
,
где
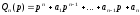 ,
а
,
а