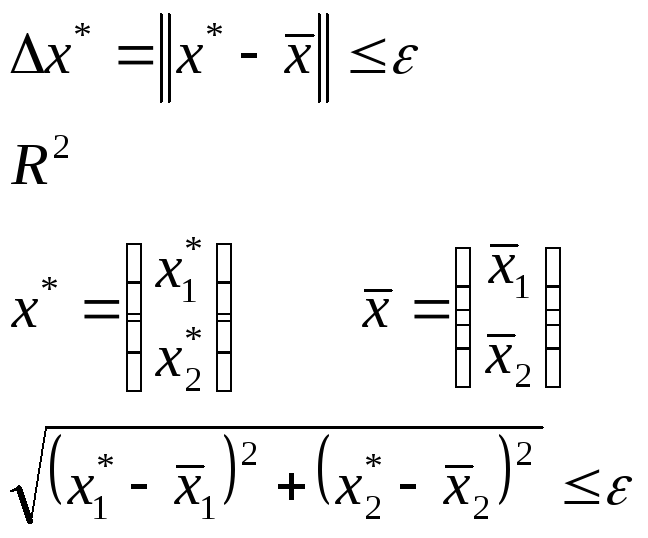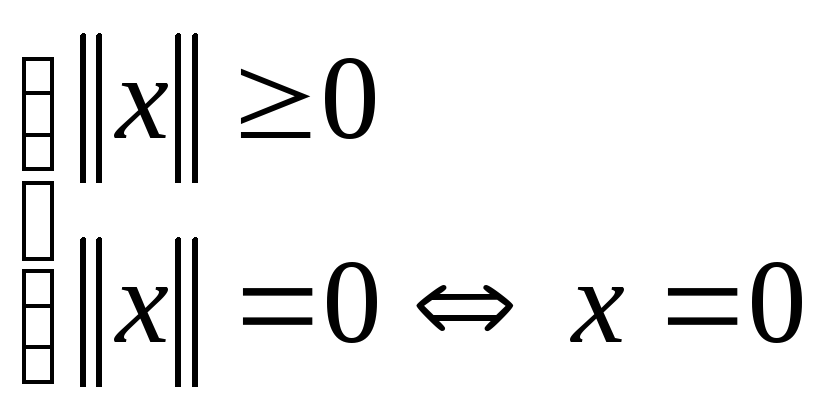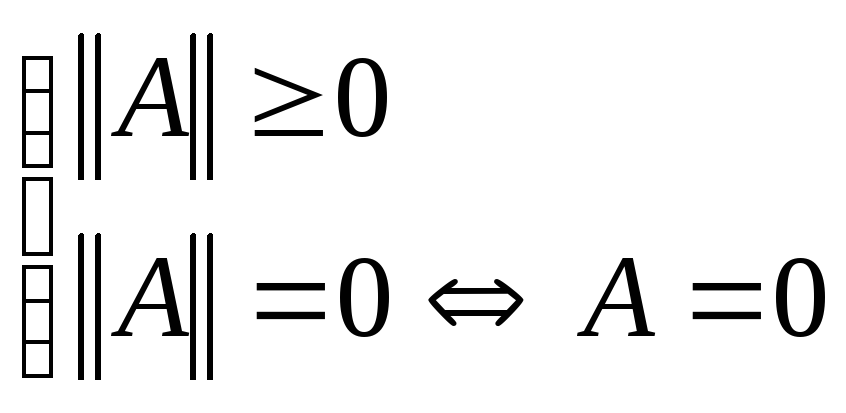- •Численные методы
- •Правила округления.
- •Оценка погрешностей арифметических операций и функций.
- •Оценка погрешности функции одной переменной.
- •Лекция № 2. Особенности машинной арифметики. Корректность вычислительной задачи.
- •Принцип равных влияний.
- •Представление данных в эвм.
- •Нелинейные уравнения.
- •Метод простой итерации (мпи).
- •Универсальный алгоритм приведения уравнения к виду,
- •Лекция № 5.
- •Обусловленность задачи решения слау.
- •Лекция № 6. Решение слау прямыми методами. Метод Гаусса и его модификации.
- •Модификации метода Гаусса.
- •Lu-разложение или матричная форма метода Гаусса.
- •Применение прямых методов для решения слау.
- •Метод простой итерации.
- •Лекция № 8.
- •Лекция № 9.
- •Лекция № 10.
- •Итерационный процесс
- •С чебышевским набором параметров.
- •Многочлены Чебышёва.
- •Вспомогательная задача.
- •Чебышёвский процесс для вычисления решения системы.
- •Лекция № 11.
- •Лекция № 13.
- •Нелинейная задача метода наименьших квадратов.
- •Метод Фибоначчи.
- •Градиентные методы.
Универсальный алгоритм приведения уравнения к виду,
удобному для итерации.
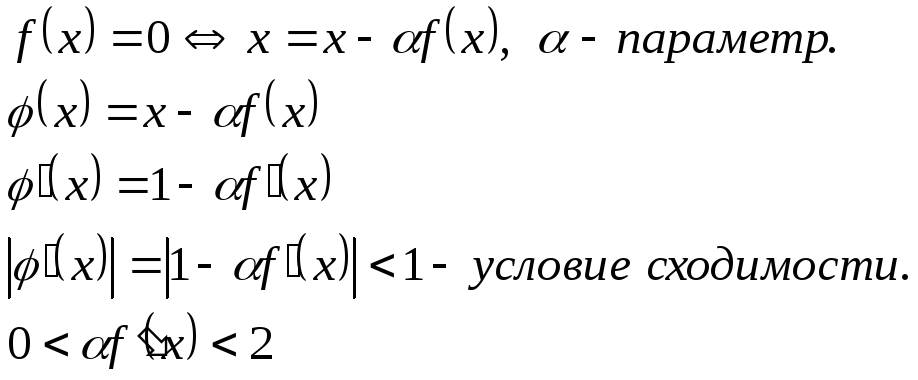
![]() на отрезке
локализации должна быть знакопостоянна.
на отрезке
локализации должна быть знакопостоянна.
Знак ![]() должен совпадать со знаком производной
должен совпадать со знаком производной
![]() на
на ![]() .
.
О птимальное
значение параметра
птимальное
значение параметра![]() .
.
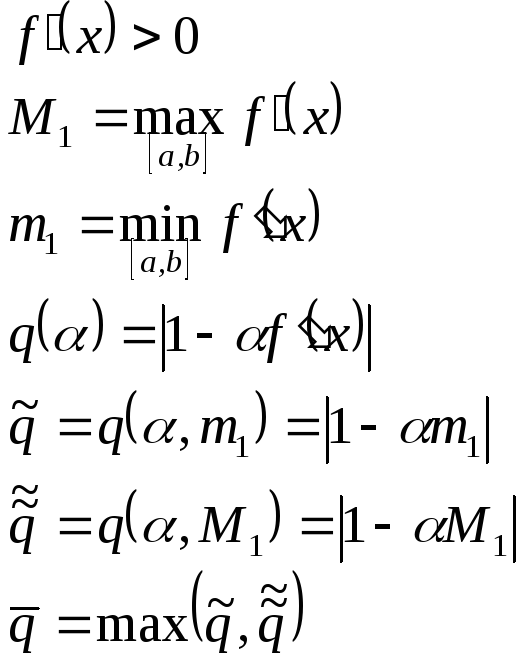
![]() –минимальное
значение функции
–минимальное
значение функции ![]() .
.
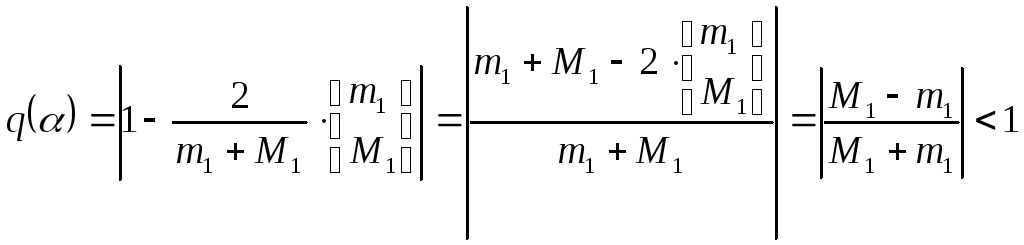
Метод простой итерации с оптимальным выбором параметра.
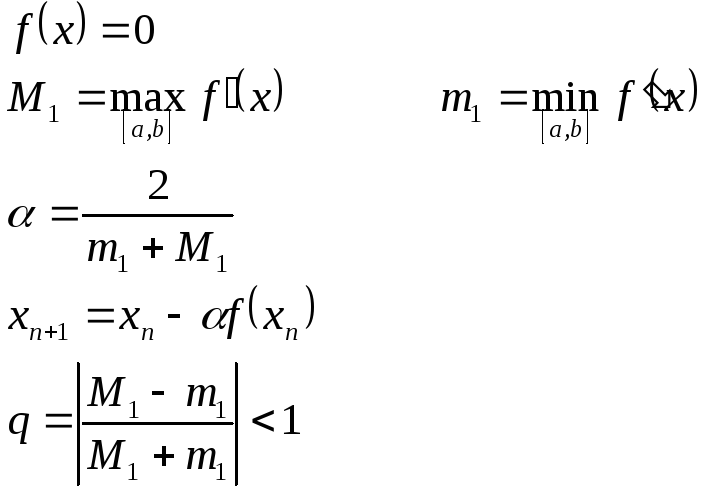
Критерий окончания
![]()
Пример.
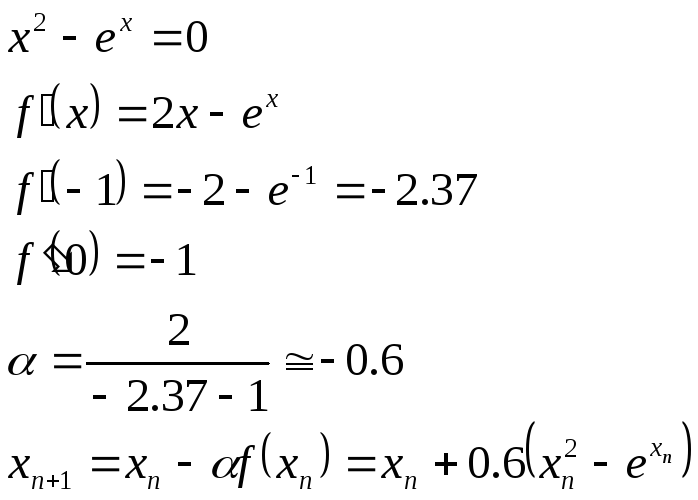
![]() метод сходится.
метод сходится.
![]()
Метод Ньютона (метод касательных).
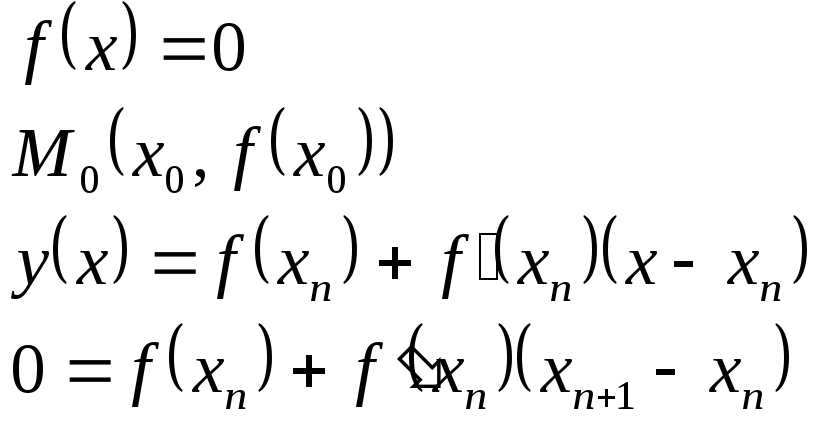
Расчётная формула метода Ньютона:
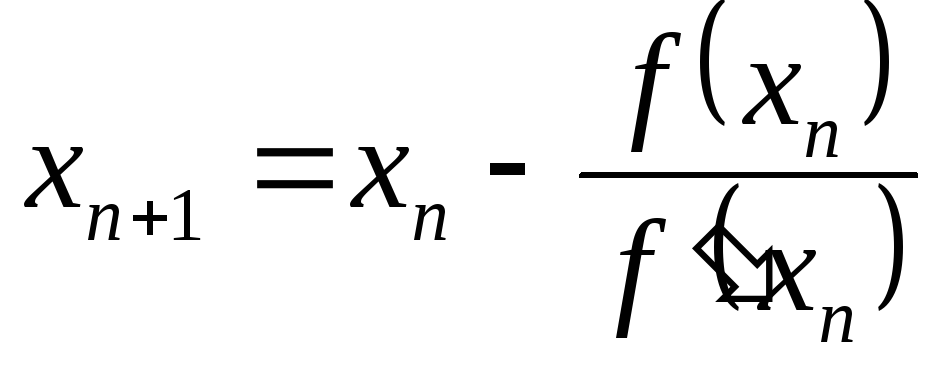

Лекция № 4.
 РЕШЕНИЕ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
РЕШЕНИЕ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Метод секущих.
Основывается также на замене произведения разностью отношений, z является точкой итерационной последовательности.
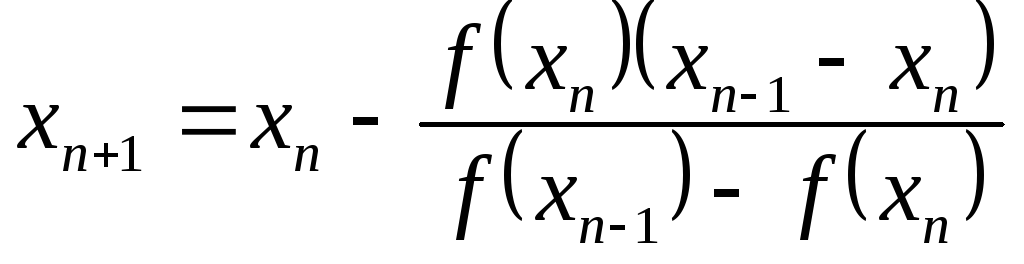
Точки ![]() и
и ![]() называются
стартовыми точками и выбираются любыми
из области локализации.
называются
стартовыми точками и выбираются любыми
из области локализации.
Пусть ![]() – простой корень уравнения, функция
– простой корень уравнения, функция ![]() дважды непрерывно дифференцируема и
вторая производная в точке корня равна
0, тогда при произвольном выборе начальных
приближений
дважды непрерывно дифференцируема и
вторая производная в точке корня равна
0, тогда при произвольном выборе начальных
приближений ![]() и
и ![]() из
из ![]() окрестности корня метод секущих с
порядком
окрестности корня метод секущих с
порядком ![]() .
.
Трудоёмкость метода секущих меньше трудоёмкости метода Ньютона.
Метод Стеффенсона.
![]() является методом
второго порядка точности p
= 2.
является методом
второго порядка точности p
= 2.
Обусловленность задачи вычисления корня уравнения.
![]()
![]() –коэффициенты
возрастания начальной погрешности.
–коэффициенты
возрастания начальной погрешности.
Точность достигнута,
если ![]() .
.
Определение 1.
Из-за вычислительной погрешности существует такой интервал, называемый интервалом неопределённости корня, внутри которого невозможно определить, какое число является корнем. Длина интервала называется радиусом неопределённости корня.
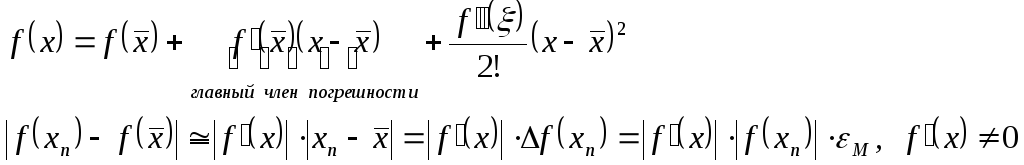
![]() –радиус
неопределённости корня.
–радиус
неопределённости корня.
Вывод:
Если
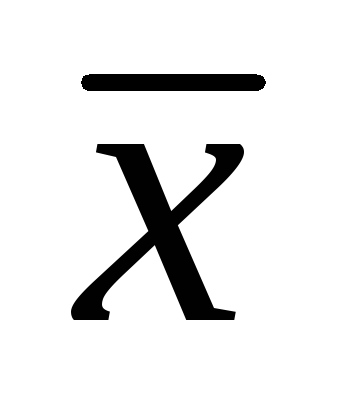 – простой корень, т. е.
– простой корень, т. е. 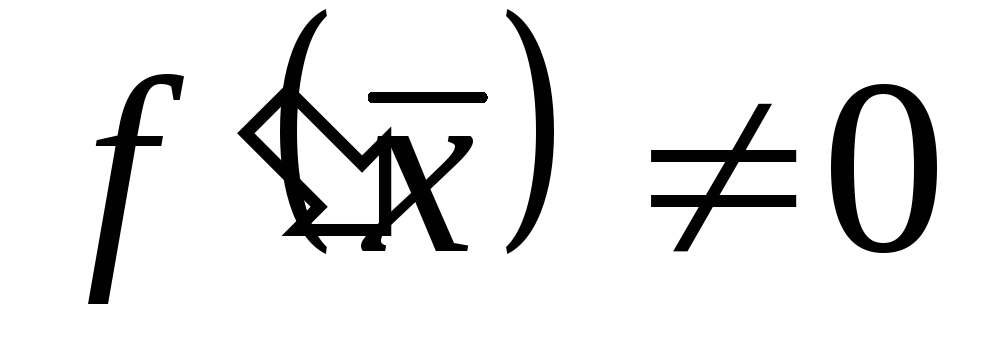 ,
то задача хорошо обусловлена.
,
то задача хорошо обусловлена.Если корень кратный, т. е.
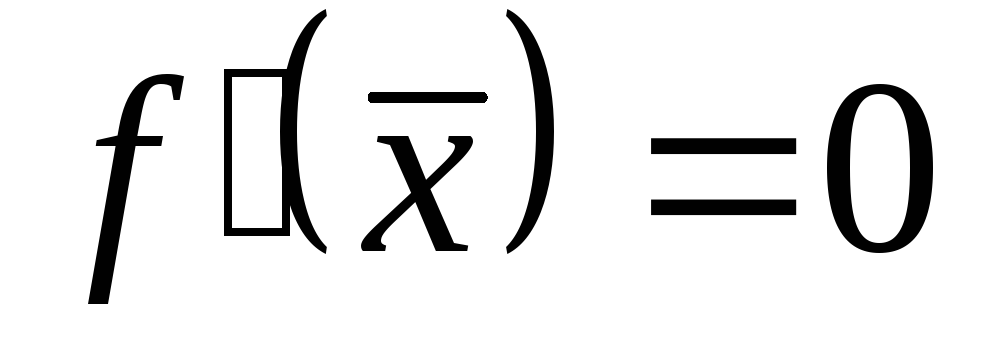 ,
то задача становится плохо обусловленной.
,
то задача становится плохо обусловленной.
![]() –корень кратности
m
–корень кратности
m
![]()
![]()
Задача. Найти радиус неопределённости для кратного корня.
Алгоритм для нахождения кратного корня:
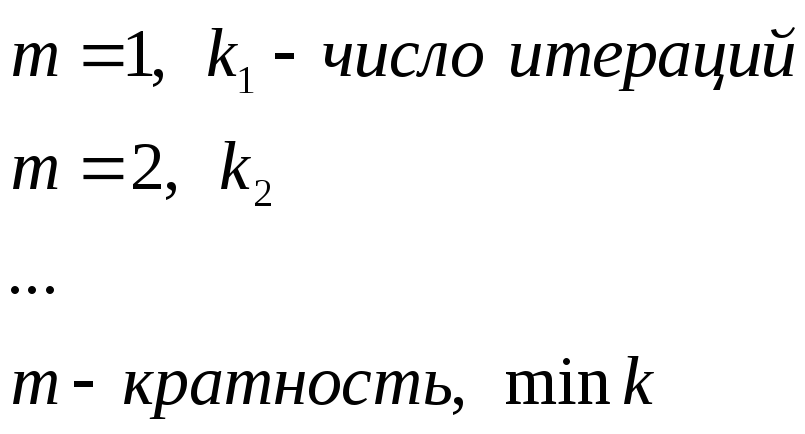
Лекция № 5.
 РЕШЕНИЕ
СИСТЕМ ЛИНЕЙНЫХ
РЕШЕНИЕ
СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ).
Вспомогательные сведения.
Основные задачи вычислительной математики:
Решение СЛАУ.
Нахождение собственных чисел и собственных векторов.
Обратная матрица.
Вычисление определителя.
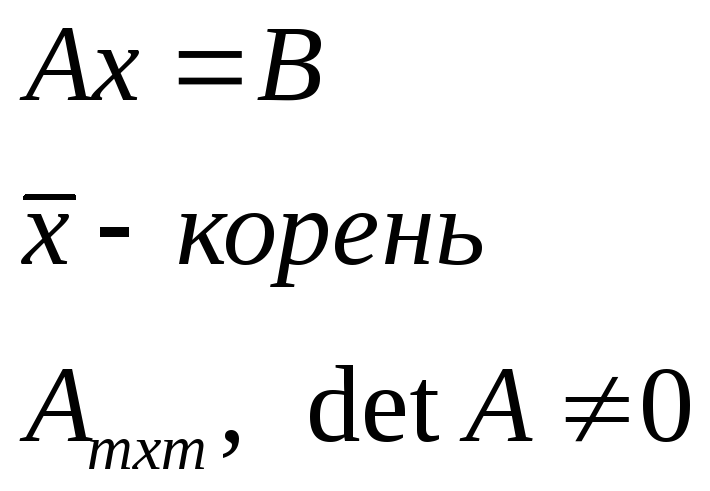
Постановка задачи о приближенном решении уравнения.
![]()
![]() –точное решение
(неизвестно).
–точное решение
(неизвестно).
Требуется найти
вектор ![]() – приближенное решение с точностью
– приближенное решение с точностью ![]() .
.
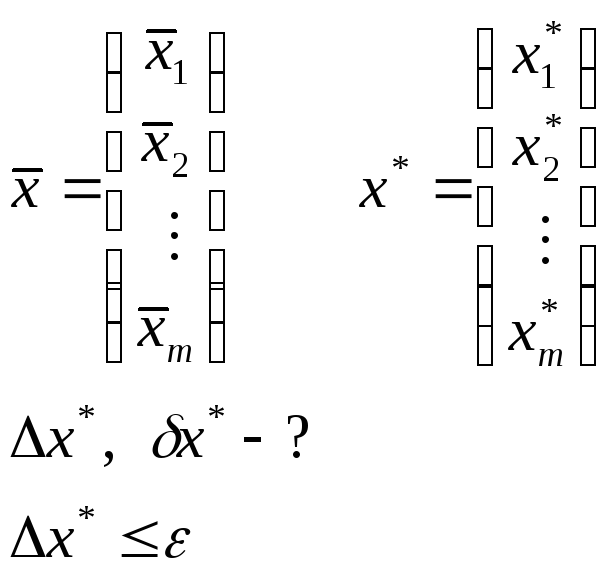
Определение 1.
Будем говорить,
что в ![]() введена норма
вектора,
если
введена норма
вектора,
если ![]() сопоставляется число
сопоставляется число ![]() ,
удовлетворяющее аксиомам:
,
удовлетворяющее аксиомам:
Наиболее употребительные нормы:
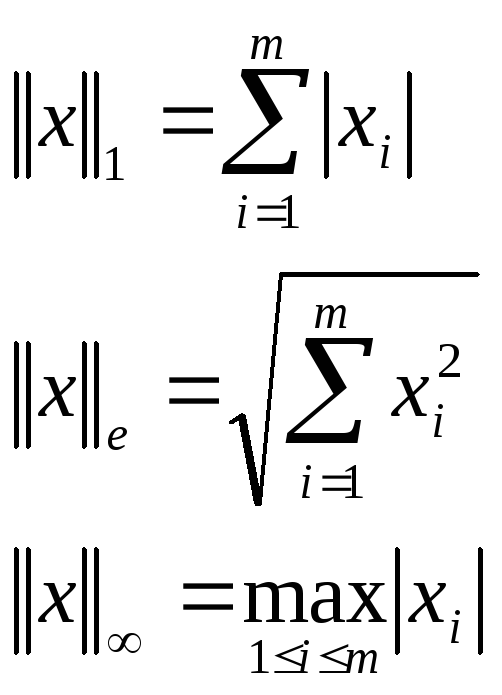
Пример.
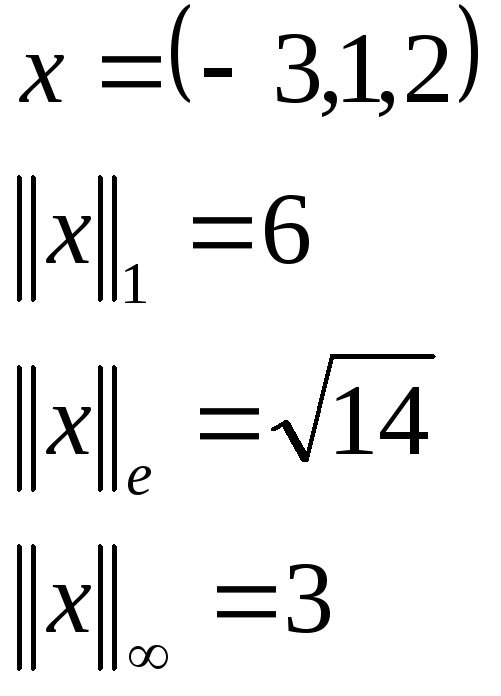
Определение 2.
Под погрешностями вектора будем понимать:
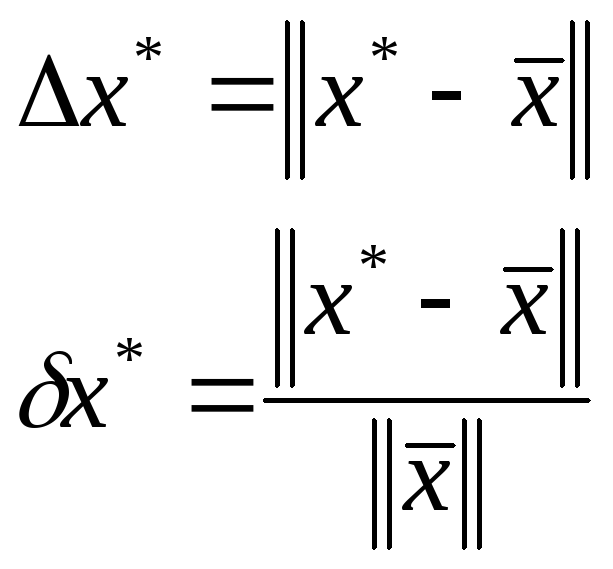
Справедливо следующее соотношение для норм векторов:
![]() –размерность
пространства.
–размерность
пространства.
Пусть рассматривается
последовательность приближений ![]() .
.
Будем говорить,
что эта последовательность сходится к
![]() по норме, если
по норме, если ![]() .
.
Всюду далее конкретизация нормы не существенна, т. к. сходимость одной влечёт сходимость по остальным.
Определение 3.
Подчинённой
нормой матрицы
А называется число, определяемое ![]() .
.
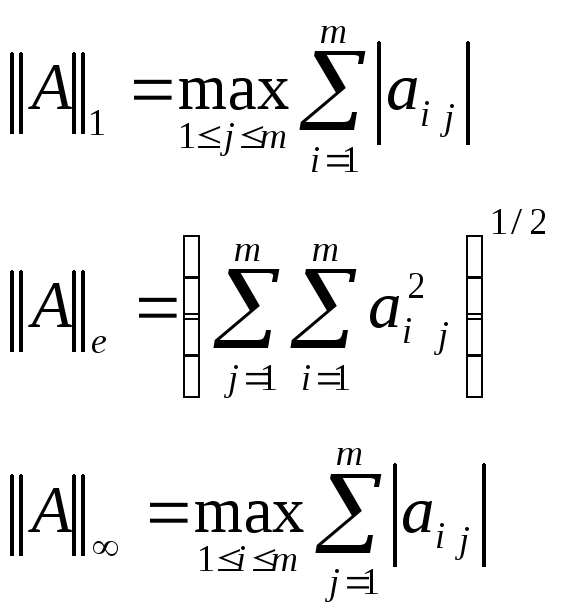
Пример.
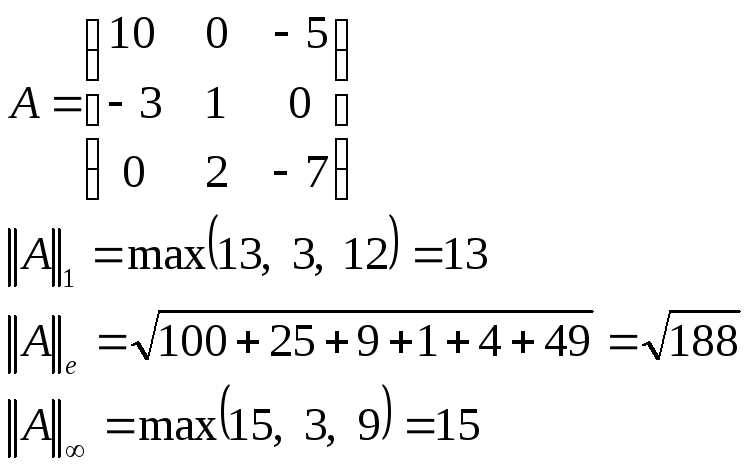
Введённая таким образом норма удовлетворяет следующим аксиомам нормы матрицы:
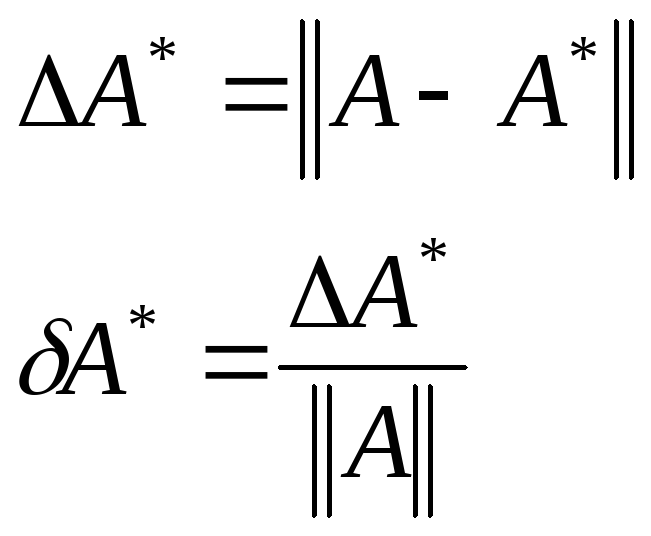
Имеем систему ![]() Найти не сможем,
т. к. искажена и A
и b.
Будем решать
Найти не сможем,
т. к. искажена и A
и b.
Будем решать ![]() .
.
Р ассмотрим
задачу о нахождении приближенного
решения
ассмотрим
задачу о нахождении приближенного
решения![]() ,
выбрав евклидову норму вектора
,
выбрав евклидову норму вектора ![]() .
.