
Ravnotochnye_izmerenia_vriant_18
.docx-
Общие сведения
Равноточными измерениями называют однородные результаты, полученные в процессе измерений инструментами одного класса точности при одинаковых условиях. Измерения в свою очередь бывают: необходимые и избыточные.
-
Формулы равноточных измерений
|
Виды функции |
Оценка точности |
|
|
|
|
|
|
|
|
|
|
|
|
если
 ,
тогда
,
тогда
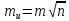

Наиболее надежным – вероятнейшим значением измеренной величины, полученных по результатам ряда равноточных измерений, является среднее арифметическое значение, которое определяется по формуле:
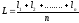 =
=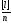
Среднее арифметическое значение называют также арифметической срединой. Значения средней арифметической:
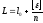
Средняя квадратическая
погрешность арифметической средины М
в 2 раз меньше средней квадратической
погрешности одного измерения
 и рассчитывается по формуле:
и рассчитывается по формуле:
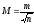
Средняя квадратическая
погрешность одного измерения
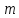 ,
вычисляется по формуле:
,
вычисляется по формуле:

Средняя квадратическая погрешность одного измерения. Определяемая по разностям двойных равноточных измерений определяется по формуле:
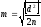
в
том случае, когда исключена из разностей
систематическая погрешность
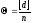 ,
то средняя квадратическая погрешность
определять по формуле арифметической
средины:
,
то средняя квадратическая погрешность
определять по формуле арифметической
средины:

Имеется ряд
равноточных измерений
 ,
,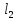 ,…,
,…,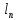 одной
и той же величины. Из результатов
измерений получено среднее арифметическое
значение. В таком случае вводят
вероятнейшие поправки, которые вычисляются
по формуле
одной
и той же величины. Из результатов
измерений получено среднее арифметическое
значение. В таком случае вводят
вероятнейшие поправки, которые вычисляются
по формуле

Для поправок характерны следующие свойства:
Это свойство поправок используется для контроля правильности вычислений.

Контроль вычислений
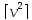
 ,
,


Если Lполучено с округлением, то контроль не выполняется, тогда выполняется равенство

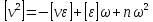

-
Решение задач
1 задача
Найти среднюю квадратическую погрешность суммы углов n-угольника, если углы измерялись с точностью:
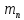 =
=
Дано:
 =
1″
=
1″
n = 8
Решение:
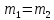 =
=
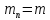 ,
применяется формула:
,
применяется формула:
 =
=
подставляем данные нам значение и получаем:
 =5=1″
=5=1″ =2,8″
=2,8″
Ответ:
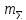 =2,8″
=2,8″
2 задача
Произвести обработку ряда равноточных измерений угла: 1)найти среднее арифметическое значение, 2)среднюю квадратическую погрешность одного измерения, 3) среднюю квадратическую погрешность арифметической средины.
|
№ |
Измерение |
Ε |
υ |
υ² |
υε |
|
1 |
173˚43΄19˝ |
0 |
9 |
81 |
0 |
|
2 |
173˚43΄23˝ |
4 |
5 |
25 |
20 |
|
3 |
173˚43΄41˝ |
22 |
-13 |
169 |
-286 |
|
4 |
173˚43΄25˝ |
6 |
3 |
9 |
18 |
|
5 |
173˚43΄32˝ |
13 |
-4 |
16 |
-52 |
|
6 |
173˚43΄23˝ |
4 |
5 |
25 |
20 |
|
7 |
173˚43΄33˝ |
14 |
-5 |
25 |
-70 |
|
∑ |
|
63 |
0 |
350 |
-350 |
-
Найдем приближенное значение измеряемой величины:

 =
173˚43΄19˝
=
173˚43΄19˝ -
Выбрав его, вычисляем остатки по формуле:
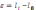
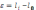 =173˚43΄19˝-173˚43΄19˝=0˝.
Также вычисляем остатки для оставшихся
измерений и заполняем колонку.
=173˚43΄19˝-173˚43΄19˝=0˝.
Также вычисляем остатки для оставшихся
измерений и заполняем колонку. -
Используя формулу среднего арифметического значения
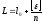 ,
получаем : L
= 173˚43΄19˝+63/7=173˚43΄28˝
; ω=0
−погрешность округления.
,
получаем : L
= 173˚43΄19˝+63/7=173˚43΄28˝
; ω=0
−погрешность округления.
-
Формула для вычисления средней квадратической погрешности m , имеет вид:
 ,
,
где поправку где
поправка
 ,
рассчитываем по формуле:
,
рассчитываем по формуле:
 =
= ;
подставляем:
;
подставляем:
 =
173˚43΄32˝-173˚43΄19˝=
- 4, таким образом рассчитываем для
оставшихся измерений заполняем колонку.
=
173˚43΄32˝-173˚43΄19˝=
- 4, таким образом рассчитываем для
оставшихся измерений заполняем колонку.
-
[
 ]=
n* ω = 7 * 0 =
0
]=
n* ω = 7 * 0 =
0 -
[
 ]=-[υε]+(
]=-[υε]+(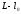 )[υ]
= > средняя квадратическая погрешность
находится по формуле:
)[υ]
= > средняя квадратическая погрешность
находится по формуле:
 ;
подставляем наши значения и получаем:
;
подставляем наши значения и получаем:

-
Средняя квадратическая погрешность арифметической средины М в
 раз меньше m одного
измерения:
раз меньше m одного
измерения:

Ответ:1)L= 173˚43΄,19˝; 2)m = 8˝; 3)M = 3,02
3 задача
Найти среднюю квадратическую погрешность одного измерения угла по разностям двойных равноточных измерений. Исключив систематическую погрешность.
|
№ |
L’ |
L’’
|
|
|
∂ |
∂ ² |
|
|
1 |
218˚18΄18˝ |
218˚18΄19˝ |
-1 |
1 |
5,7 |
32,49 |
-57 |
|
2 |
151˚26΄09˝ |
151˚26΄02˝ |
7 |
49 |
13,7 |
187,69 |
95,9 |
|
3 |
203˚31΄56˝ |
203˚31΄51˝ |
5 |
25 |
11,7 |
136,89 |
58,5 |
|
4 |
76˚48΄24˝ |
76˚48΄27˝ |
-3 |
9 |
3,7 |
13,69 |
-11,1 |
|
5 |
165˚56΄04˝ |
165˚56΄59˝ |
-55 |
3025 |
-48,3 |
2332,89 |
2656,5 |
|
6 |
133˚33΄29˝ |
133˚33΄26˝ |
3 |
9 |
9,7 |
94,09 |
29,1 |
|
7 |
221˚08΄38˝ |
221˚08΄41˝ |
-3 |
9 |
3,7 |
13,96 |
-11,1 |
|
∑ |
|
|
-47 |
3127 |
-0,1 |
2811,43 |
2812,8 |
-
Среднюю квадратическую погрешность одного измерения определяем по разностям двойных равноточных измерений:
 ″.
″. -
Для исключения из разностей систематическую погрешность находим : θ
 =-47/7=
- 6.7
=-47/7=
- 6.7 -
После этого определяю среднюю квадратическую погрешность по формуле:

-
Найдем разности двойных равноточных измерений по формуле:
 =
L’-L’’,
подставляем
=
L’-L’’,
подставляем
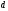 =
=218˚18΄18˝-216˚18΄19˝=
-4, таким образом нахожу разности для
оставшихся измерений и заполняю колонку.
=
=218˚18΄18˝-216˚18΄19˝=
-4, таким образом нахожу разности для
оставшихся измерений и заполняю колонку. -
Для того чтобы исключить систематическую погрешность, определяем их по
формуле:
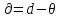 ,
подставляем
,
подставляем
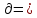 -1 – (- 6,7) = 5,7, таким образом находим
систематическую погрешность для
оставшихся измерений и заполняем
колонку.
-1 – (- 6,7) = 5,7, таким образом находим
систематическую погрешность для
оставшихся измерений и заполняем
колонку.
-
Используем формулу
 ,
подставляем и получаем
,
подставляем и получаем

Делаем
проверку используя формулу:
[∂²]=[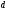 ²]-[
²]-[ ]²/n=[
]²/n=[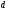 ²]-θ[
²]-θ[ ]
]
2811,43 = 3147- 2209/7 = 3127- ( - 6,7 ) * ( - 47 )
2811,43 = 2811,5 = 2812,1



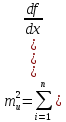



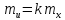



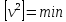

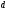
 ²
² ∂
∂