ОГЛАВЛЕНИЕ
|
1 ОБЩИЕ СВЕДЕНИЯ |
3 |
|
2 ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ |
3 |
|
3 РЕШЕНИЕ ЗАДАЧ |
5 |
|
3.1 Задача 1 |
5 |
|
3.2 Задача 2 |
6 |
|
ЗАКЛЮЧЕНИЕ |
|
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
|
1 Общие сведения
Неравноточными называют измерения производимые не в одинаковых условиях с различными дисперсиями, и средними квадратическими погрешностями.
-
Обработка результатов неравноточных измерений
При
обработке неравноточных измерений
вводят новую характеристику точности
измерения, называемую весом измерения:
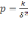
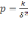 ,
,
где k - произвольно выбранное число, единое для всех весов, участвующих в решении задачи; δ - дисперсия результата измерения.
Так
как точное значение 
 никогда
не известно, вес принимают:
никогда
не известно, вес принимают: 
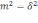 ,
где m -средняя
квадратическая погрешность, по результам
измерений.
,
где m -средняя
квадратическая погрешность, по результам
измерений.
Так как k - произвольное число, то вес дает представление о точности результата только при сравнении его с весами других результатов.
1 Свойство весов: Отношение весов не изменяется, если все веса увеличить или уменьшить в одно и то же число раз.
2 Свойство весов:
Веса двух измерений обратно пропорциональны квадратам средних квадратических погрешностей этих измерений.
Из определения веса следует, что равноточные измерения имеют равные веса, а неравноточные — неравные веса. Приняв вес одного измерения за единицу, т. е. p = 1, вес среднего арифметического становится равным числу измерений P=n.
Если известны
веса аргументов функции, то можно найти
и вес самой функции. При k=1
вес р равен
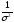 ,
откуда
,
откуда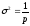 .
Величину
.
Величину
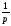 называют
обратным весом.
называют
обратным весом.
Среднее
весовое значение или арифметическая
средина вычисляется:
 =
=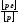
 ,
а с приближенными значениями эта
формула имеет вид: L=
,
а с приближенными значениями эта
формула имеет вид: L=
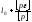 ,
где
,
где
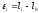 .
.
В
случае, когда из результатов измерений
получено среднее весовое значение,
вводят поправки: υ=L-
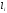 .
.
Средняя
квадратическая погрешность единицы
веса через вероятнейшие поправки:
 .
.
Средняя
квадратическая погрешность общей
арифметической средины имеет вид:
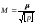 ,
выражение средней квадратической
погрешности общей арифметической
средины через вероятнейшие поправки:
,
выражение средней квадратической
погрешности общей арифметической
средины через вероятнейшие поправки:
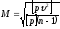 -
-
Контроль
вычисления
 :
:
-
Средняя квадратическая погрешность единицы веса, если в разностях нет систематической погрешности:
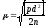 .
В случае их наличия они исключаются
из разностей. Систематическая погрешность
обозначается Θ и
определяется по формуле:
.
В случае их наличия они исключаются
из разностей. Систематическая погрешность
обозначается Θ и
определяется по формуле:
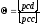 .
При расчете двойных линейных
измерений, если в разностях нет Θ,
средняя квадратическая погрешность
единицы веса:
.
При расчете двойных линейных
измерений, если в разностях нет Θ,
средняя квадратическая погрешность
единицы веса:
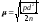 ,
если она имеется, то
,
если она имеется, то
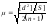 ,
где
,
где
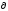 =
d-
Θ.
=
d-
Θ. -
Контроль вычисления:
-
[d]= [Θ] [
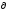 ]=[d]=[
Θ]=0.
]=[d]=[
Θ]=0. -
-
-
3 Решение задач
-
Задача 1