Тема II. Основные понятия и уравнения гидродинамики

2.1. Основные определения кинематики жидкости. Неразрывность

А. Основные определения. Из предыдущего известно, что состояние какого-либо объема покоящейся жидкости полностью определяется величинами внутренних напряжений (гидростатических давлений) в отдельных его точках, возникающих в результате воздействия на жидкость внешних сил. Для характеристики состояния движущейся жидкости недостаточно знать только распределение давлений. Необходимо знать также, с какими скоростями движется жидкость в различных точках, то есть задачей гидродинамики является определение скоростей и давлений жидкости в различных точках потока и в различные моменты времени t. В общем случае вектор скорости u и давление p являются функциями четырех переменных:

, .

Если скорость и давление в любой фиксированной точке потока остаются неизменными во времени (т. е. являются функциями только координат х, у, z), то течение называется установившимся. Пример установившегося течения – истечение жидкости из бака под постоянным напором. Если скорость и давление меняются со временем, то течение – неустановившееся. Например, если при истечении из бака убыль жидкости не восполняется, то напор, скорость и давление в любой точке постепенно уменьшаются, это течение неустановившееся.

Мгновенную картину течения наглядно представляют линии тока (рис. 6, а). В каждой точке линии тока вектор скорости направлен по касательной к ней. При установившемся течении линии тока совпадают с траекториями частиц, при неустановившемся течении они могут не совпадать.

Если провести линии тока через все точки элементарно-малого контура, то образованная ими поверхность ограничитэлементарную струйку (рис. 6, б). В элементарной струйке жидкость течет, не смешиваясь с соседними объемами, так как, по определению, векторы скорости направлены по касательной к ее поверхности. Площадь сечения струйки dS выбирают достаточно малой для того, чтобы вектор скорости u оставался в этом сечении неизменным по величине.

Объем жидкости, протекающей через сечение струйки в единицу времени, называют элементарным расходом dQ. Он равен произведению длины вектора скорости на площадь сечения струйки

. (II.1)

Размерность расхода – м³/сек.

Рассматривая поток жидкости, такой, например, как в трубе или канале, допустимо считать, что он состоит из большого числа элементарных струек. В этом случае сечение потока (в гидравлике его называют «живым сечением») равно сумме сечений элементарных струек. Расход потока есть сумма расходов струек, в пределе – интеграл по площади сечения:

. (II.2)

При известном расходе Q легко определить среднюю скорость потока V в данном сечении:

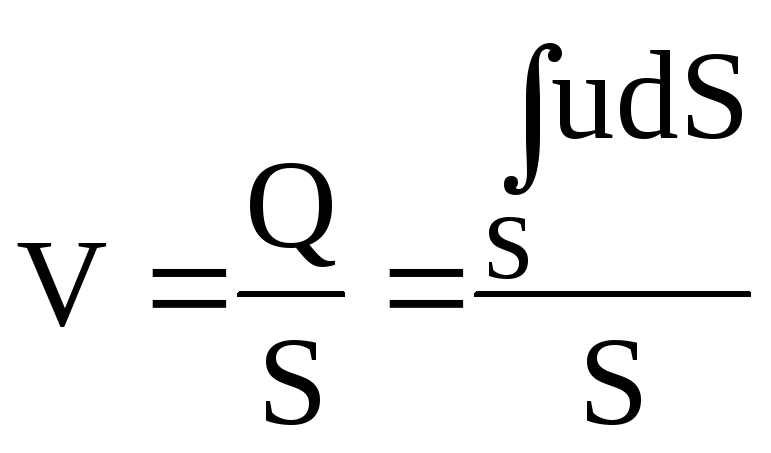. (II.3)

Для характеристики торможения потока твердыми стенками кроме сечения S в гидравлике вводятся еще понятия смоченного периметра χ – периметр сечения в пределах соприкосновения с твердыми стенками трубы или канала, и гидравлического радиуса R, причем

. (II.4)

Размерность смоченного периметра и гидравлического радиуса – м.

Как видно из выражения (II.4), гидравлический радиус характеризует компактность сечения потока. Для круглой трубы радиуса r, например, гидравлический радиус

, если d – диаметр трубы, то .

Если в потоке между какими-нибудь двумя его сечениями количество жидкости не пополняется извне и не убывает (нет источников и стоков), то масса протекающей через эти два сечения жидкости сохраняется неизменной. Математически этот принцип выражается уравнением неразрывности (это название подчеркивает, что в рассматриваемых сечениях поток сплошной, не содержит полостей и разрывов).

Наиболее просто записывается уравнение неразрывности для установившегося одномерного течения, в котором скорость меняется только в направлении одной продольной координаты. Примерами одномерного течения являются элементарная струйка, движение в трубе и канале. Для элементарной струйки несжимаемой жидкости принцип сохранения массы выражается через постоянство объемного расхода (II. 1) в струйке (рис. 6, б):

. (II.5)

Очевидно, что для потока в трубе или канале необходимо постоянство расхода, вычисленного по средней скорости w_ср:

. (II.5а)

В случае одномерного течения сжимаемой жидкости принцип неразрывности требует постоянства массового расхода, который равен произведению объемного расхода на плотность ρ:

. (II.6)

Одномерное течение несжимаемой жидкости является предметом изучения гидравлики. В отличие от нее гидродинамика рассматривает более сложные двухмерные и трехмерные потоки, в которых скорость может изменяться в направлении двух дли трех координатных осей.

Б. Уравнение неразрывности для трехмерного течения несжимаемой жидкости.

Из курса математического анализа известно, что непрерывную функцию, имеющую все непрерывные производные, можно разложить в ряд Тейлора. Поэтому можем для скорости и давления записать следующие разложения

; .

Или, пренебрегая малыми величинами высшего порядка, при стремлении Δl к нулю:

; .

Здесь u и скорость и ее первая производная в точкеl;

–скорость в точке ;

p и – давление и его первая производная в точкеl;

–давление в точке .

Эти разложения мы будем пользоваться в дальнейшем при составлении указанных дифференциальных уравнений.

Выберем в потоке фиксированный в пространстве элементарный объем в форме параллелепипеда с ребрами dx, dy, dz (рис. 7). Пусть у левой грани этого объема составляющая скорости в направлении оси x равна u_x. По достижении правой грани эта составляющая может измениться и стать равной

.

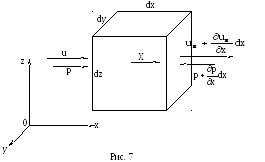
Через левую грань за единицу времени втекает внутрь параллелепипеда объем жидкости, равный произведению нормальной составляющей скорости на площадь грани: w_xdydz.

Через правую грань вытекает объем

.

Суммарное поступление жидкости через левую и правую грани равно разности:

.

Аналогично получим, что через грани, перпендикулярные оси у (задняя и передняя грани на рис. 7), Суммарное поступление жидкости внутрь параллелепипеда равно . Через грани, перпендикулярные оси z (нижняя и верхняя на рис. 7), поступает объем. Здесьu_y и u_z – составляющие скорости в направлении осей y и z. Если внутри параллелепипеда нет источников и стоков, т.е. объем жидкости в нем не меняется, то суммарный расход через все грани равен нулю:

.

Разделив последнее равенство на объем параллелепипеда dxdydz, получим уравнение неразрывности в дифференциальной форме

. (II.7)

При выводе уравнения неразрывности мы не учитывали сжимаемости жидкости. В наиболее общем случае неустановившегося движения сжимаемой жидкости уравнение неразрывности имеет вид (приводится без вывода):

. (II.7)