
Кручение и сложное напряженное состояние
.docxМинистерство высшего и среднего специального образования СССР
________
Московское ордена Ленина, ордена Октябрьской Революции и
ордена Трудового Красного знамени
высшее техническое училище им. Н.Э.Баумана
А.С.Газарян, Л.Г.Парилова, В.Н.Шитиков
Утверждены
редсоветом МВТУ
КРУЧЕНИЕ И СЛОЖНОЕ НАПРЯЖЕННОЕ СОСОЯНИЕ
Методические указания
к выполнению домашнего задания
по курсу «Сопротивления материалов»
Под редакцией З.М.Конюшко
Москва 1981
Данные методические указания издаются в соответствии с учебным планом
Рассмотрены и одобрены кафедрой К-5 19.12.80 г., Методической комиссией факультета К и Учебно-методическим управлением
Рецензент к.т.н. доц. Хавов В.М.
Графические работы выполнены И.Д.Кисенко
© Московское высшее техническое училище им. Н.Э.Баумана
Настоящие указания предназначены для студентов дневного и вечернего отделений и содержат образцы выполнения расчетно-графических домашних заданий по разделу «Кручение и сложно напряженное состояние».
При работе над домашним заданием следует учитывать общие рекомендации и указания по выполнению расчетно-графических работ, изложенные в разработке А.С.Газарян, Г.П.Клюева, Н.А.Сухова. Расчетно-графические работы по сопротивлению материалов. Растяжение – сжатие – М.: Изд. МВТУ, 1980.
1. Кручение
Задача 1.1
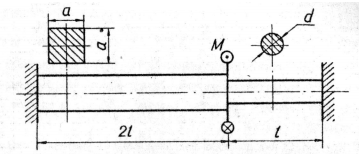
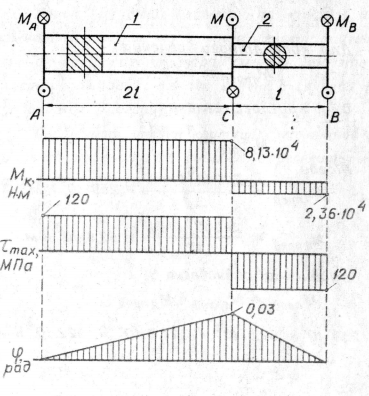
Определить размера a из условия равнопрочности участков бруса, изображенного выше.
Определить допускаемую величину момента Mдоп, используя метод расчета по допускаемым напряжениям. Найти предельное значение момент Мпред. Материал бруса идеальный упруго-пластичный.
Построить эпюры крутящих моментов Мк, наибольших касательных напряжений τmax и углов поворота сечений φ при М = Мдоп.
Дано: τТ
= 240 МПа ; 
nT =2,0 ;
d = 100 мм ;
l = 1 м ;
G = 8∙104 МПа.
Решение
1. Определение размера a
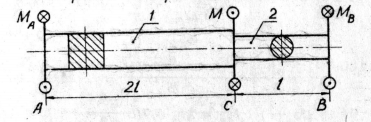
а) Уравнение равновесия
МА + МВ = М.
Задача один раз статически неопределима.
б) Уравнение перемещений
φСА
= φСВ
,
 =
=
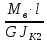 ;
;
JK1
= β∙a4
=
0,141 a4,
JK2
= Jp2
=
 ;
;
 =
=
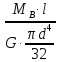 :
, МА
= МВ ∙
0.718
:
, МА
= МВ ∙
0.718
 . (1)
. (1)
в) Условие равнопрочности
τmax1
= τmax2
; τmax
=
 ;
;
WK1
= αa3
= 0,208a3,
WK2
= Wp2
=
 ;
;
 =
=
 ;
с учетом зависимости (1)
;
с учетом зависимости (1)
 =
=
 ;
a = 1,475 d ,
;
a = 1,475 d ,
a = 1,475 ∙ 100 = 147,5 мм ≈ 148 мм.
2. Определение Мдоп
а)
Условие прочности τmax
≤
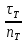 ;
;
τmax
2
=
 =
=
 ;
;
MB
=
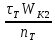 =
=
 = 2,36∙104
Н∙м
.
= 2,36∙104
Н∙м
.
Из (1) МА
= МВ
∙ 0,718
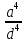 =
=
= 2,36 ∙ 104
∙ =0,718( )4
= 8,13 ∙ 104 Н∙м
.
)4
= 8,13 ∙ 104 Н∙м
.
б) Уравнение равновесия
МА + МВ = Мдоп ;
Мдоп = 8,13 ∙ 104 + 2,36 ∙ 104 = 10,49 ∙ 104 Н∙м .
3. Построение эпюр Мк, τmax, φ
a) Крутящие моменты
М1 = МА = 8,13 ∙ 104 Н∙м ,
М2 = МВ = 2,36 ∙ 104 Н∙м .
б) Наибольше касательное напряжение
τmax1
=
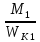 =
=
 = 120 ∙ 106
= 120 ∙ 106
 = 120 МПа ,
= 120 МПа ,
τmax1
=
 =
=
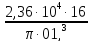 = 120 ∙ 106
= 120 ∙ 106
 = 120 МПа .
= 120 МПа .
в) Углы поворота сечений
φА = 0 ;
φ1
= φА
+
 = φA
+
= φA
+
 ; ᵶ1
ϵ
[ 0 , 2l
]
; ᵶ1
ϵ
[ 0 , 2l
]
φ1 |ᵶ1=0 = φA = 0 ;
φC
= φ1
|ᵶ1=2l
= φA
+
 =
=
 = 0,03 рад ;
= 0,03 рад ;
φ2
= φС
+
 = φС
+
= φС
+
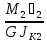 ; ᵶ2
ϵ
[ 0 , l
]
; ᵶ2
ϵ
[ 0 , l
]
φВ
= φ2
|ᵶ2=l
= φС
+
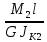 = 0,03 -
= 0,03 -
 = 0 .
= 0 .
4. Определение предельного момента Мпред
Конструкция потеряет несущую способность, когда сечения первого и второго уастков будут полностью охвачены пластическими деформациями, т.е.
М1 = М1пред М2 = М2пред

Для квадратного сечения
М1пред
=
 ,
,
для круглого сечения
М2пред
=
 .
.
Тогда
М1пред
=
 = 259 ∙ 103 Н∙м
,
= 259 ∙ 103 Н∙м
,
М1пред
=
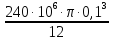 = 62,8 ∙ 103 Н∙м
.
= 62,8 ∙ 103 Н∙м
.
Уравнение равновесия
Мпред = М1пред + М2пред =
= 259 ∙ 103 + 62,8 ∙ 103 = 321,8 ∙ 103 =
= 321,8 ∙ 103 ≈ 322 ∙ 103 Н∙м .
Задача 1.2

Валик AD, защемленный по концам и имеющий круглое поперечное сечение диаметром d, нагружается парой сил М. При этом жесткий рычаг 1, закрепленный в сечении В, упирается в ограничители 2.
Построить эпюры крутящих моментов Мк и углов поворота сечений φ. Определить коэффициент запаса по текучести nT.
Дано: М = 25 Н∙м ,
l = 0,2 м ,
d = 10 мм ,
L = 0,1 м ,
Δ = 1 мм ,
G = 8 ∙ 104 МПа ,
τТ = 150 МПа .
Решение
1. Раскрытие статической неопределимости
При упоре рычага 1 в ограничители 2 на валик AD в сечении В передает пара сил МВ

Уравнение статического равновесия
∑Мᵶ = 0, – МА – МВ + М – МD = 0. (1)
Задача дважды статически неопределима.
Уравнение перемещения
φв
=
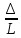 ,
,
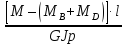 =
=
 , (2)
, (2)
φDA=
0, –
 +
+
 –
–
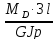 = 0 . (3)
= 0 . (3)
Преобразую (1), (2) и (3), получим
МА + МВ + МD = M ,
MB
+ MD
= M
–
 ,
,
MB + 3MD = 2M .
Здесь Jp
=
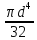 , d
= 0,01 м, M
= 25 Н∙м,
, d
= 0,01 м, M
= 25 Н∙м,
 = 3,93 Н
= 3,93 Н

 МА
+ МВ
+ МD
= 25 ,
МА
= 3,93 Н,
МА
+ МВ
+ МD
= 25 ,
МА
= 3,93 Н,
MB
+ MD
= 21,07 ,
![]() МВ =
6,60 Н∙м,
МВ =
6,60 Н∙м,
MB + 3MD = 50 ; МD = 14,47 Н∙м
2. Определение крутящих моментов
Участок АВ
МАВ
= МА
= 3,93 Н∙м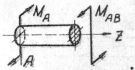
(направлен против часовой стрелки).
Участок ВС
МВС
= МА
+ МВ
=
= 3,93 + 6,6 = 10,53 Н∙м
(направлен против
часовой стрелки).
Участок CD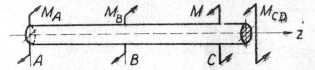
МCD = MA + MB – M = 3,93 + 6,6 – 25 = – 14,47 Н∙м (направлен по часовой стрелке).
3. Определение углов поворота φ Начало отсчета выбираем в сечении А.
φА = 0;
φв
= φВА
=
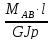 =
=
 = 0,01 рад;
= 0,01 рад;
φС
= φВ
+ φСВ
= φВ
+
 ,
,
φС
= 0,01 +
 = 0,0368 рад;
= 0,0368 рад;
φD
= φC
+ φDC
= φC
+
 ,
,
φD
= 0,0368 –
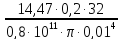 = 0 .
= 0 .

4. Определение коэффициента запаса
nT
=
 , τmax
=
, τmax
=
 , Wp
=
, Wp
=
 .
.
τmax
=
 = 73,7 МПа ,
= 73,7 МПа ,
nT
=
 = 2,035 .
= 2,035 .
Задача 1.3
Трубка и вал,
выполненные из одного материала, закре-
плены левыми торцами, а правыми соединены
с жесткой крышкой. К трубке приложена
пара сил М.
Построить эпюры крутящих
моментов МК,
наибольших касательных напряжений τmax
и углов поворота сечений φ для вала и
трубки. Найти предельную величину
момента Мпред.
Материал идеальный упруго-пластичный
Дано: М = 600
Н∙м ,
l = 1 м, Dср = 40 мм,
δ =
 Dср
, d
=
Dср
, d
=
 Dср,
Dср,
τT = 200 МПа, G = 8 ∙ 104 МПа .
Решение
1. Кручение в области упругих деформаций
Рассмотрим отдельно
трубку и вал.
а) Уравнение равновесия для трубки МАтр – М + Х = 0 (1)
б) Уравнение равновесия для вала МАв = Х. (2)
Задача один раз статически неопределима
в) Уравнение перемещений
φВАтр
= φВАв
,
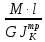 +
+
 =
=
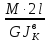 ; (3)
; (3)
JКтр
= Jpтр
=
 =
=
 , JКв
= Jpв
=
, JКв
= Jpв
=
 =
=
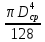 .
.
Решая уравнения (1), (2), (3), получаем
X =
 ,
,
 ,
,

г) Построение эпюр
Трубка Крутящие моменты


Наибольшие касательные напряжения
τmax
=
 ,
,
 ;
;


Углы поворота сечений
φА
= 0 ; φD
= φA
+
 =
=

φВ
=
φD
+

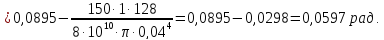

Вал
Крутящий момент
МAB = X = 150 Н∙м.
Наибольшее касательное напряжение
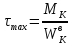 ,
,
 ;
;

Углы поворота сечений
φА
= 0 ; φB
= φA
+
 =
=

2. Определение предельного момента Мпр
Рассмотрим два
возможных случая потери несущей
способности.


Реализует…


