113. 1. Лабораторная работа «Исследование системы экстремального управления».

        2. Цель работы: Изучение характера и основных закономерностей процессов управления объектами с экстремальными характеристиками, ознакомление с принципом построения экстремального регулятора.

        3. Теоретическая часть

        5. Под системой экстремального управления понимается система, в которой решение поставленной задачи осуществляется путем достижения экстремума некоторой функции и ее поддержания в условиях дрейфа.

        6. Отличительным признаком таких систем является наличие у объекта управления статической характеристики, с явно выраженным экстремумом, достигаемым при определенных значениях входных сигналов. Эта характеристика во времени не остается неизменной. Под действием различных причин может поменяться ее профиль, положение экстремума, экстремальное значение. Однако неизменным остается сам факт наличия экстремума. Система экстремального управления должна по мере изменения статических свойств объекта или ухода выходной величины объекта из зоны экстремума, изменять входные величины таким образом, чтобы они соответствовали экстремальной точке и обеспечивали работу объекта в экстремальном режиме.

        7. В основу синтеза одномерных экстремальных систем закладываются разнообразные методы.

        8. Для всех методов характерно то, что нарастание или убывание входного сигнала изменяется всякий раз, когда при поиске минимума выходной сигнал x(t) начинает возрастать и при поиске максимума убывать. Очевидно, что для организации такого характера изменения входного сигнала необходимо знание градиента производной функции . При этом реверс исполнительного механизма (ИМ), который вызывает изменениеu(t) осуществляется каждый раз при изменении знака этой производной. Производную можно определить методом синхронного детектирования, который заключается в следующем.

        9. Пусть имеется функция x(u). Допустим, что ее аргумент получает малое приращение . В результате получим функции.Умножим эту функцию на приращение. Тогда получим величину. РазложимZ в ряд Тейлора в окрестности точки u=u₁ и воспользовавшись малостью ограничим разложение квадратичными членами:

        10. (*)

        11. Найдем среднее значение величины Z. С этой целью процесс Z можно подать на устройство (фильтр), выполняющее операцию усреднения

        12. (**)

        13. где Т - время усреднения.

        14. Так как аргумент u является постоянным, то после подстановки (*) в (**), получим

        15. 

        16. В качестве приращения , которое называется поисковым сигналом выберем гармонический процесс вида

        17. При этом .

        18. В результате имеем

        19. 

        20. Т.е. среднее значение процесса Z пропорционально искомой производной. Схему принципа синхронного детектирования можно увидеть на рисунке 4.4.1

        21. 

        22. Рисунок 4.4.1 - Схема синхронного детектирования

        24. Если объект является многомерным, т.е. то искомые составляющие градиента этой функцииможно определить поставив на выходе объекта управления параллельноm синхронных детекторов СД.

        25. Схему одномерной экстремальной системы, построенную по принципу синхронного детектирования можно представить в виде рисунка 4.4.2.

        27. 

        29. Рисунок 4.4.2 – Одномерная экстремальная система

        31. В данном случае экстремальный регулятор реагирует на знак с помощью релейного элемента РЭ, выдающего сигнал на исполнительный механизм, обеспечивающий изменениеu(t) с постоянной скоростью в сторону достижения экстремума x(u).

        32. Если РЭ отсутствует, то будем иметь классическую схему движения к экстремуму по методу градиента. В этом случае оказывается возможным убрать усредняющий фильтр Ф и возможность его функции на ИМ, который в силу своей природы реализует операцию интегрирования и вследствие этого выполняет функции фильтра высоких частот.

        33. Анализ изложенных принципов одномерного экстремального управления показывает, что в процессе работы выходной сигнал u(t) совершает периодические изменения от U_min до U_max относительно экстремального значения. При этом Т_к - период колебаний.

        34. Качество работы экстремальной системы характеризуют тремя показателями: наибольшим отклонением входного сигнала от его экстремального значения, (амплитуда колебаний на выходе а_m ) периодом колебаний входного сигнала и средним значением отклонения выходного сигнала объекта x(t) от его экстремального значения, называется потерями на рысканье (поиск) P.

        35. 

        36. При инерционных объектах управления в их составе условно выделяют безынерционную часть с экстремальной (статической) характеристикой x(t) и линейное звено, отражающее инерционные свойства объекта рисунок 4.4.3

        38. 

        40. Рисунок 4.4.3 – линейное звено

        42. Процесс g(t) на входе нелинейного звена существенно отличается по форме от процесса u(t) в безынерционном случае. Процесс движения к экстремуму с инерционным объектом оказывается более сложным по сравнению с безынерционным. При этом деформации и временные запаздывания процессов могут привести к нарушению устойчивости поиска экстремума.

        43. В работе исследуются процессы, происходящие в экстремальной системе с безынерционным и инерционным объектом рисунок 4.4.4 (а, б). Имитация дрейфа осуществляется подачей сигнала g(t).

        44. 

            а)

        45. 

            б)

        47. Рисунок 4.4.4 – Экстремальные системы (а – безынерционная, б - инерционная)

        49. Порядок выполнения работы

1. Собрать структурную схему, соответствующую рисунок 4.4.4 а. Один из вариантов ее представления в MatLab представлен на рисунке 4.4.5.

1. 

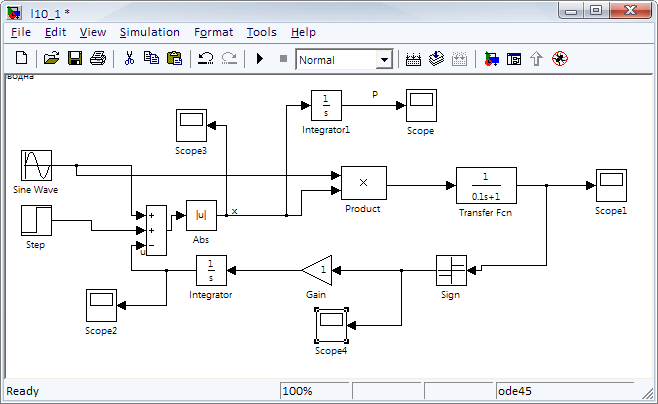
3. Рисунок 4.4.5 – Схема безынерционной экстремальной системы

5. Принять, а=0.2, ω =10Гц, g(t)=1. Наблюдать и зарисовать процессы x(t) при различных k(10,20,50). Определить a_m, Т_k, Р.

2. Собрать схему, которая представлена на рисунке 4.4.6, что соответствует системе рисунок 4.4.4б. Повторить п.1, приняв, Т=0.01 сек.

56. 

58. Рисунок 4.4.6 - Схема инерционной экстремальной системы

3. При k=10 задаваясь различными значениями Т от 0.01 и выше влияние инерционности объекта на параметры предельного цикла a_m, Т_k , а также потери на поиск Р.

4. Изменяя инерционность объекта Т найти границу устойчивости алгоритма поиска.

1. Контрольные вопросы

1. Что такое экстремальные системы?

2. В чем заключается поиск экстремума по методу градиента?

3. В чем заключается поиск экстремума по методу детектирования?

4. Что такое потери на рысканье?

5. Что такое поисковый сигнал?

6. Назовите основные критерии качества экстремальной системы

7. Каким образом процесс после прохода инерционного звена отличается от процесса после прохода неинерционного?

1. Содержание отчета

1. Структурные схемы исследуемых систем.

2. Графики процессов для всех вариантов.

3. Числовые данные оценки качества процессов.

4. Выводы.

Заключение

2. В ходе дипломного проектирования были достигнуты следующие результаты:

• Произведен анализ существующих аналогов обучающих систем как общего назначения, так и систем построенных на базе пакетов обработки электрических сигналов; выделены основные свойства присущие интерактивным обучающим системам;

• Разработан комплекс лабораторных работ, состоящий из одиннадцати лабораторных работ;

• Рассмотрены вопросы экономико-организационного плана: приведено обоснование необходимости создания лабораторного комплекса, произведен расчет затрат на его проектирование и изготовление, определена цена комплекса;

• Рассмотрены вопросы охрана труда при организации рабочего места пользователя ЭВМ.

66. Выполнение задачи в полной мере отвечают требованиям задания на дипломное проектирование комплекса лабораторных работ по ТАУ.

67. Данный комплекс является открытым для дополнения и модификации, также данное приложение может использоваться как среда проектирования автоматизированных систем управления технологическими процессами на базе средств, предоставляемых MatLab.

Библиографический список

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования: Наука, 1975.-768с.

2. Воронов А.А., Основы теории автоматического регулирования: Наука, 1977.-519с.

3. Зайцев Г.Ф., Теория автоматического управления и регулирования: Высшая школа, 1988.-432с.

4. Сергиенко А.Б., Цифровая обработка сигналов: Питер, 2003.-604с.

5. Чураков Е.П., Оптимальные и адаптивные системы: Учеб. Пособие для вузов. – М.: Энергоатомиздат, 1987.-256с.

6. Черных И.В., SIMULINK среда инженерных приложений: Диалог – Мифи, 2004.-248с.

7. Справочник по теории автоматического управления/ А.Г. Александров и др.; под ред. А.А. Красовского.-М: Наука,1987-711с.

8. Применение имитационного моделирования при проектировании систем управления реального времени: Учеб.пособие/Д ревс Ю.Г., Золотарев В.В., Шитова Н.А.;МИФИ-М.,1982.-72с.

9. Вохрышев В.Е. Цифровое моделирование релейных и оптимальных по быстродействию систем: Учеб. Пособие/ Самар.гос.техн.ун-т. –Самара:СамГТУ 1993.-104с.

10. Первозванский А.А. Курс теории автоматического управления/ Учеб.пособие для вузов-М. Наука 1986.-615с.