Лабораторна робота №8

Обробка результатів сукупних та опосередкованих вимірювань

Лабораторна робота № 1

Опрацювання результатів сукупних та опосередкованих вимірювань

Мета роботи: засвоїти на практиці (в лабораторних умовах) методику оцінки похибок прямих, опосередкованих, сумісних та сукупних вимірювань.

Після виконання роботи студенти повинні:

- знати види похибок, закони розподілу випадкових похибок, похибки ряду прямих, сумісних, сукупних та опосередкованих вимірювань, форми представлення результатів вимірювань;

- вміти застосовувати отримані знання при обробці ряду прямих та непрямих вимірювань, представляти результати вимірювань згідно до ДСТУ 2681-94.

Теоретичні відомості

Оцінка випадкових похибок опосередкованих вимірювань

Опосередковані вимірювання – це вимірювання, при яких шукане значення q знаходять на основі відомої залежності

де Q₁, Q₂,…, Q_m – значення, отримані при прямих вимірюваннях. По вигляду функціональної залежності F вони поділяються на дві основні групи – лінійні та нелінійні. Для лінійних опосередкованих вимірювань математичний апарат статистичної обробки отриманих результатів розроблений детально. Обробка результатів опосередкованих вимірювань виконується, як правило, методами: заснованими на роздільній обробці аргументів та їх похибок; лінеаризації; приведення; перебору.

Методика обробки результатів опосередкованих вимірювань наведена в документі МИ 2083-90 “ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей”.

Оцінка випадкових похибок опосередкованих вимірювань необхідно здійснювати за такою методикою:

1. Визначити для результатів прямих вимірювань 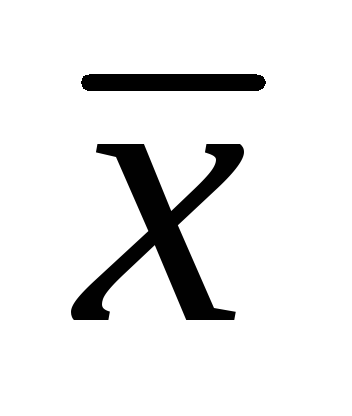і;

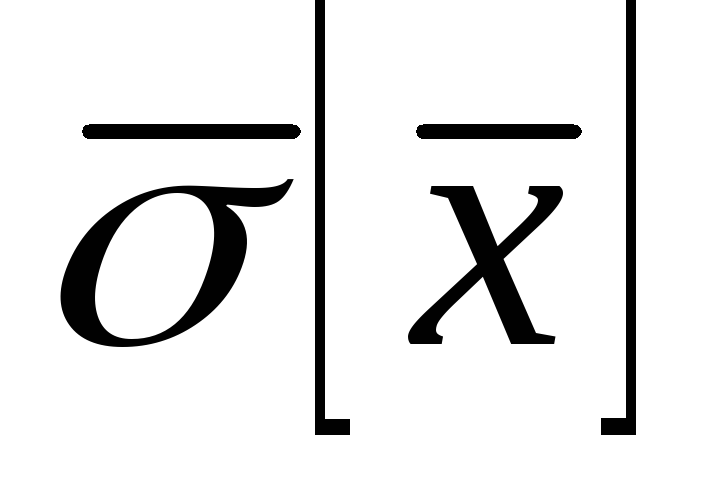2. Визначити значення невідомої величини ;

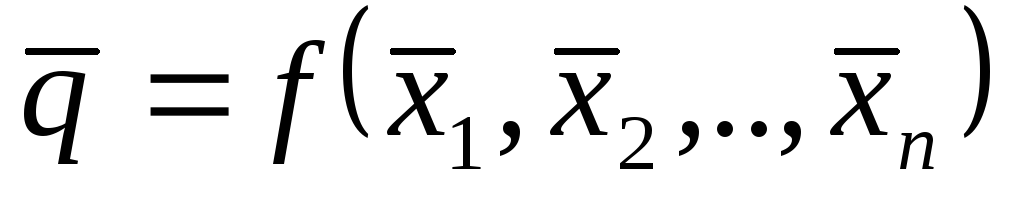3. визначити вагу кожної часткової похибки опосередкованих вимірювань

;

4. Обчислити часткові вагові похибки опосередкованих вимірювань

;

5. Знайти оцінку СКВ результату опосередкованого вимірювання

;

6. Знайти коефіцієнт k_t Стьюдента за заданою довірчою ймовірністю Р і кількістю вимірювань n.

7. Знайти граничні значення випадкової складової похибки, яку приймають за похибку опосередкованого вимірювання

;

8. Записати результат опосередкованого вимірювання:

Для визначення похибки результату опосередкованого вимірювання необхідно застосувати такі правила:

1. Якщо результат вимірювання представляється сумою або різницею двох і більше виміряних величин:

,

і похибки незалежні і випадкові, то абсолютна похибка результату може бути визначена за формулою

.

Коли похибки аргументів корельовано, значення може перевищувати отримане за попередньою формулою, але завжди буде задовольняти умову

2. Якщо кінцевий результат вимірювання представляється добутком або часткою двох і більше виміряних значень:

,

і похибки незалежні і випадкові, то відносна похибка результату опосередкованого вимірювання визначається

.

3. Якщо результат опосередкованого вимірювання є функцією однієї величини - 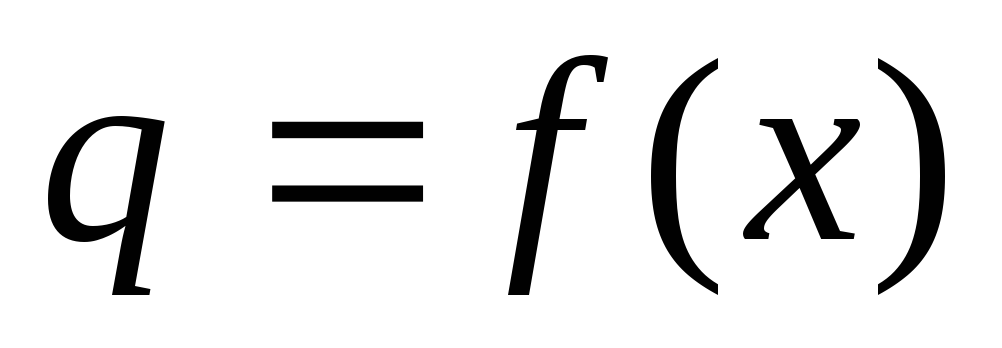, то похибка результату визначається

.

4. В загальному випадку похибка функції декількох величин 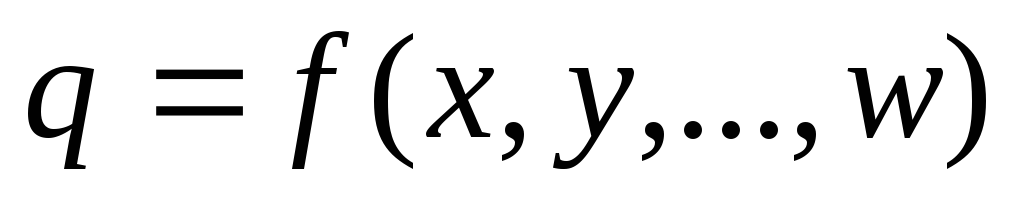, похибки яких незалежні і випадкові, знаходиться

,

але сумарна похибка ніколи не перевищить значення

.

Оцінка випадкових похибок сукупних вимірювань

При сукупних та сумісних вимірюваннях невідомі величини х_і, що підлягають безпосередньому вимірюванню, визначаються за результатами вимірювання інших величин, які функціонально пов’язані з ними

,

де і = 1,2,...n – порядковий номер невідомих величин х; j = 1,2,...,m – порядковий номер прямих вимірювань величин у.

Якщо результат прямих вимірювань Y містять випадкові похибки, то вони мають місце і в результаті сукупних вимірювань величини х_і.

Розглянемо три випадки:

1. Очевидно, що для m<n систему розв’язати неможливо.

2. Для m=n розв’язання можливе, але похибки результатів вимірювання величини х_і будуть, як і для прямих одноразових вимірювань, значними і числові значення цих похибок залишаються невідомими.

3. Для m>n систему знову неможливо розв’язати, алгебраїчно тому, що ці рівняння несумісні, оскільки праві частини рівнянь замість точних значень Y_і містять результати їхніх вимірювань у_і = Y_і + ΔY_і із випадковими похибками ΔY_і.

Проте у останньому випадку для нормального закону розподілу похибок вимірювання величини у_і можна знайти таку сукупність значень х_і , яка б з найбільшою імовірністю задовольняла б початкові умови . Це можна здійснити за допомогою методу найменших квадратів (принципу Лежандра).

Такий спосіб обробки експериментальних даних для сукупних вимірювань доцільно застосовувати для лінійних функцій. В інших випадках обробка результатів значно ускладнюється.

Тому розглянемо випадок, коли функції φ_і лінійні:

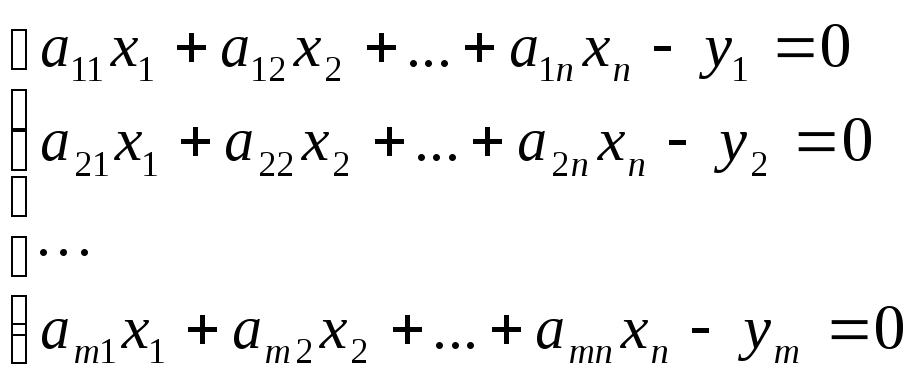
Цю ж систему представимо більш компактно

Тут індекси при коефіцієнтах показані у послідовності „рядок - стовпець”.

Ці рівняння називають умовними. Через наявність похибок праві частини умовних рівнянь дорівнюють не нулю, а деяким залишковим похибкам:

Згідно з принципом Лежандра найбільш ймовірними значеннями невідомих величин х_і для цього випадку будуть такі, для яких сума квадратів залишкових похибок мінімальна

.

Необхідною умовою такого мінімуму повинна бути рівність нулю похідних

підставивши в останню формулу значення , отримують систему нормальних рівнянь

,

яку в розгорнутому вигляді представляють так:

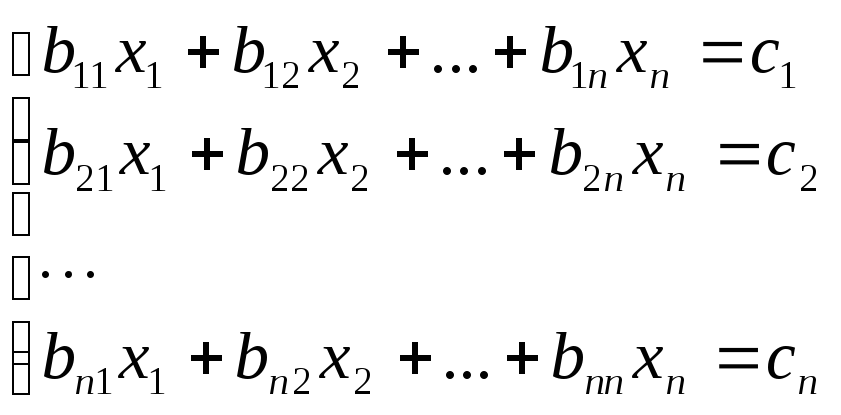
тут індекси при коефіцієнтах b показані у послідовності „рядок - стовпчик”(h-i).

Оскільки кількість нормальних рівнянь завжди дорівнює кількості невідомих, то така система має розв’язок.

Методика отримання нормальних рівнянь.

Загальний спосіб знаходження системи нормальних рівнянь полягає у знаходженні часткових похибок від кожної по кожній з невідомих х_і, перемноженням цих похідних на відповідні значення та додаванні їх для кожної невідомої х_і

Сукупність даних виразів представляє собою систему з n нормальних рівнянь.

Визначення нормальних рівнянь для n = 2.

Припустимо, що в результаті сукупних вимірювань отримано таку систему

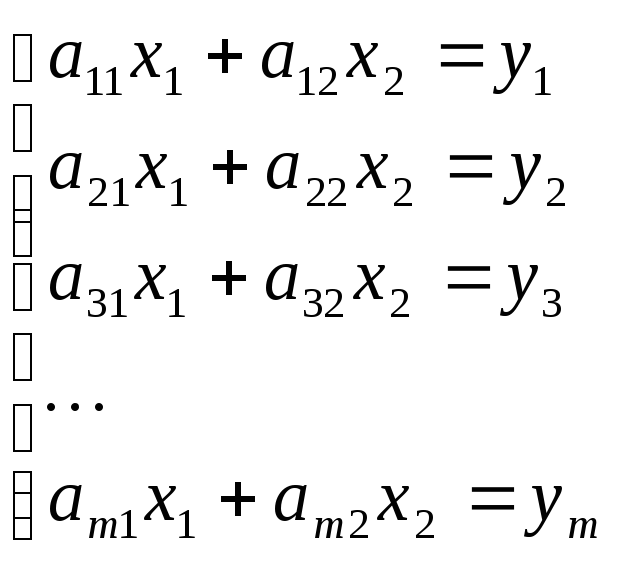
система нормальних рівнянь матиме вигляд

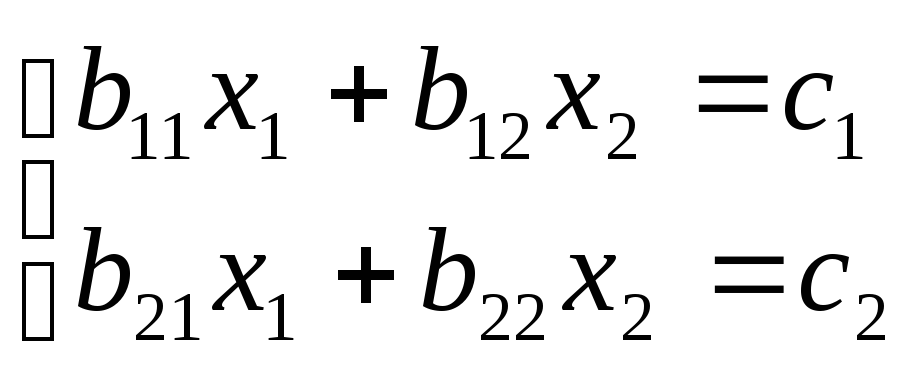
Коефіцієнти визначають із таких виразів

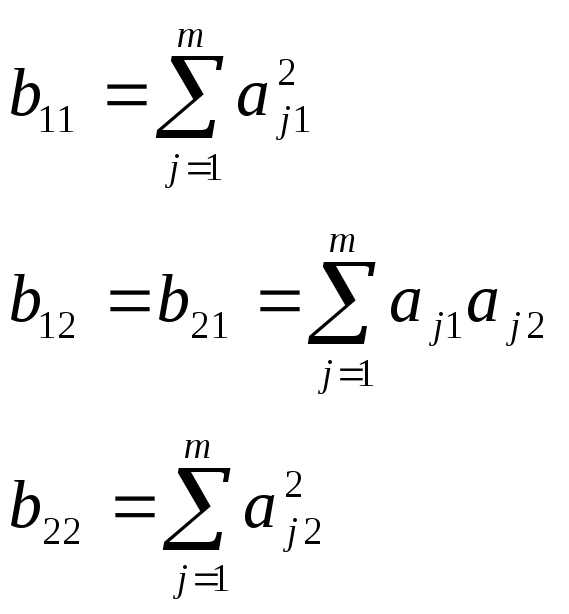
Тоді значення визначають

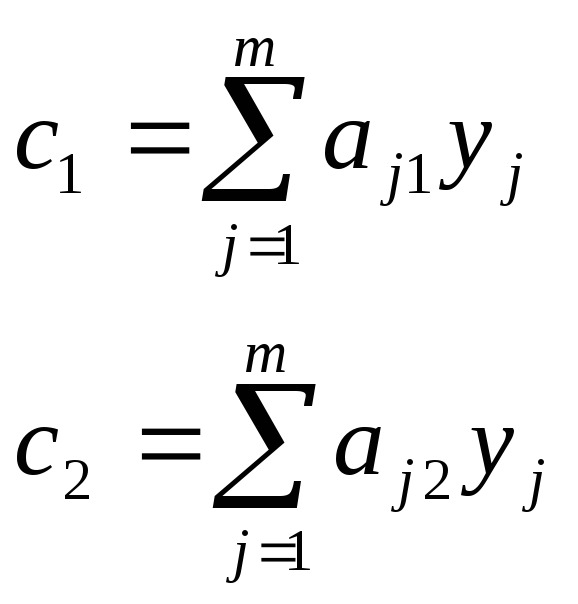
Розв’язок системи нормальних рівнянь

Якщо кількість невідомих n<=4, то систему нормальних рівнянь доцільно розв’язувати за допомогою визначників. Розглянемо розв’язування систем нормальних рівнянь для n = 2.

У цьому випадку складають та обчислюють головний визначник цієї системи рівнянь

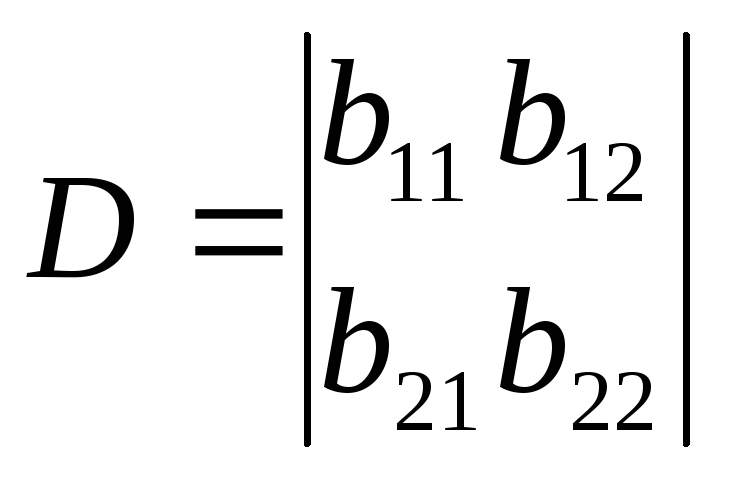
далі складають та обчислюють часткові визначники D₁ та D₂, замінивши коефіцієнти b при відповідних невідомих на члени с в системі

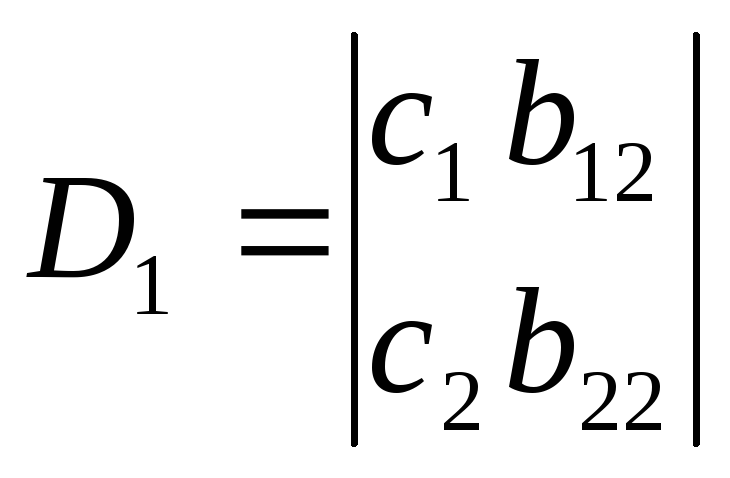
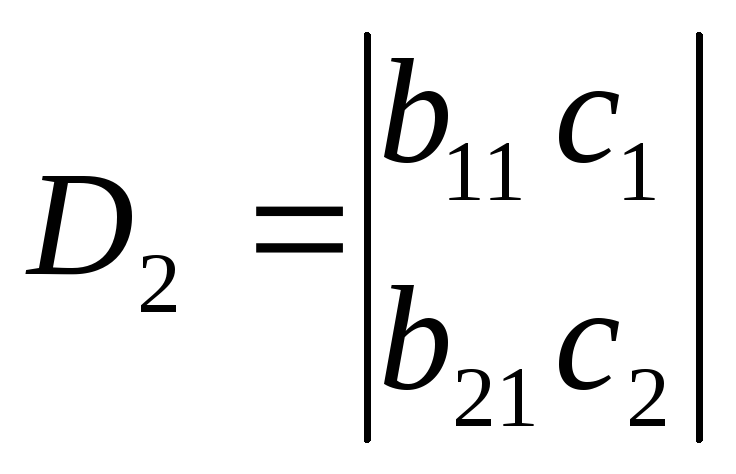
потім знаходять найбільш ймовірні значення невідомих

Середні квадратичні значення результатів сукупних вимірювань.

Після підстановки найбільш ймовірних значень до умови рівнянь, знаходять значення залишкових похибок, визначаютьта суму залишкових похибок.

Середнє квадратичне відхилення результатів сукупних вимірювань знаходять по формулі

,

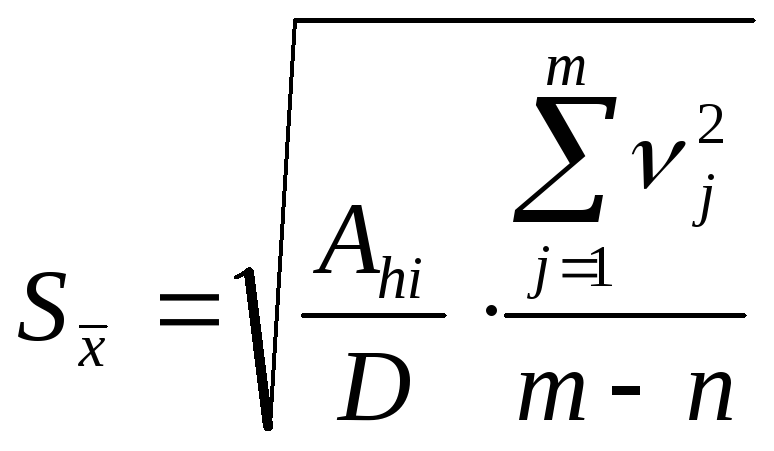де m – кількість умовних рівнянь; n – кількість невідомих; A_hi – ад’юнкти (алгебраїчні доповнення) елементів b_hi головної діагоналі визначникаD (для h = i), які отримують викривленням h – го рядка та і –го стовпця, відповідних даному елементу b_hi, з наступним домноженням на (-1)^h+1.

Для n=2 ад’юнкти: A₁₁=b₂₂; A₂₂=b₁₁.

Довірчі границі випадкової складової похибки сукупних вимірювань.

Задавшись значенням довірчої імовірності, знаходять відповідне значення коефіцієнта довіри t_p. У цьому випадку число ступенів свободи дорівнює k = m-n.

Довірчі границі випадкової похибки сукупних вимірювань становлять

.

Подання результатів вимірювань

Для подання абсолютної похибки результатів користуються однією зі стандартних форм, згідно з ДСТУ 2681-94.

Перша форма: Х; _д від - _д до + _д; Р(),

де Х- результат вимірювання в одиницях вимірюваної величини;

_д -довірчий інтервал;

Р() - довірча ймовірність.

Друга форма: ,

де - границі зміни систематичної складової похибки в одиницях вимірюваної величини;

- довірча ймовірність систематичної складової похибки;

- оцінка середнього квадратичного відхилення випадкової складової похибки в одиницях вимірюваної величини;

- закон розподілу випадкової складової похибки.

Третя форма: ,

де - оцінки середнього квадратичного відхилення систематичної і випадкової складових похибки;

- закони розподілу систематичної і випадкової складових похибки.

Четверта форма: ,

де - щільності ймовірностей систематичної і випадкової складових похибок, які подані в формі таблиць, графіків чи формул.