Удельное сопротивление аксоплазмы и саркоплазмы от 30 до 200 Ом·см;
Электрическая емкость различных клеток около 1мкФ/см2 Электрическая емкость чистого бислоя липидов 0,8мкФ/см2
С |
|
0S |
С – электрическая емкость, |
|
d |
- диэлектрическая проницаемость |
|||
изолирующей части бислоя, |
||||
|
||||
|
|
|
0 – электрическая постоянная, |
|
|
|
|
S - площадь |
Если С=0,8мкФ/см2, = 2, то d=2,2 нм
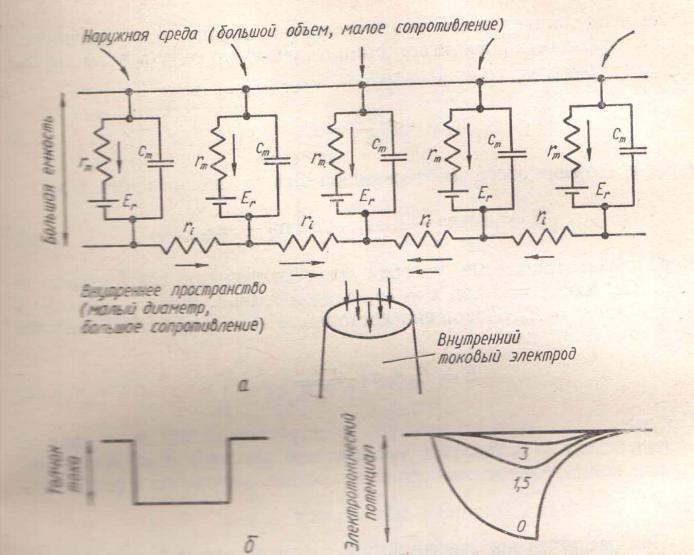
КАБЕЛЬНАЯ СТРУКТУРА
Cm емкость мембраны
rm сопротивление мембраны
ri – сопротивление аксоплазмы
Согласно закону Ома ток, текущий по осевому цилиндру:
dV |
rii |
(1) |
|
dx |
|||
|
|||
|
|
i – ток, текущий по осевому цилиндру, х – расстояние от источника тока, ri – сопротивление аксоплазмы
Выразим i:
i |
1 dV (2) |
|
|
|
|
r dx |
||
|
i |
|
Ток через мембрану i |
di |
(3) |
m dx
Исходя из 1 и 2 |
im |
1 d 2V |
(4) |
|
|
dx2 |
|||
|
r |
|||
|
|
i |
|
|
Мембранный ток складывается из двух компонентов:
im iC ii Cm |
dV |
ii |
(5) |
dt |
|||
|
|
|
Далее из 4 и 5 |
|
2 |
dV |
|
получаем |
1 d V |
(6) |
||
|
|
dx2 |
C m dt |
ii |
|
r |
|||
|
i |
|
|
|
Умножим обе части на rm
r |
d 2V |
dV |
|
m |
dx2 |
rmC m dt |
rmii (7) |
r |
|||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заменим |
|
|
rm |
2 |
|
; |
|
r C |
m |
|
|
; |
|
r i |
V |
|
|
||||||||||||||||
|
|
|
ri |
|
|
|
m |
|
|
|
|
m i |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим |
|
2 d 2V |
dV |
V |
|
(8) |
|
|
dx2 |
dt |
|
|
|
|
|
|
|
|
|
|
КАБЕЛЬНОЕ УРАВНЕНИЕ
2 d 2V dV V dx2 dt
РЕШЕНИЯ КАБЕЛЬНОГО УРАВНЕНИЯ
Решением этого уравнения является экспоненциальная зависимость:
V |
V |
|
1 |
e |
t |
|
|
|
|
||||
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Где – постоянная времени, показывающая
через сколько времени амплитуда мембранного потенциала падает в e раз .