
UP_Skorikov_724
.docx
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
Работа с математическим программным обеспечением SAGE
Отчет по учебной практике
Выполнил:
Студент гр. 724
_______ _____ Скориков И.И.
31.08.2015
Принял:
Младший научный сотрудник КИБЭВС
_______ _____ Кручинин Д.В.
31.08.2015
2015
Введение
Цель работы: научиться работать с математическим программным обеспечением SAGE.
1 Задание
Необходимо выполнить двадцать одно задание учебной практики пятого варианта в математическом программном обеспечение SAGE.
2 Теоритический материал
Sage – это бесплатное и свободно распространяемое математическое программное обеспечение с от-крытыми исходными кодами для исследовательской работы и обучения в самых различных областях включая алгебру, геометрию, теорию чисел, криптографию, численные вычисления и другие. Как модель разработки Sage, так и условия его распространения и использования выбраны в соответствии с принципами открытой и совместной работы: мы собираем машину, а не переизобретаем колесо. Одной из основных целей Sage является создание доступной, бесплатной и открытой альтернативы Maple, Matematica, Magma и MATLAB.
Для написания расчета используется язык программирования Python. Можно подключать сторонние библиотеки и создавать собственные.
3 Ход работы
3.1 Задание №1
Для
вычисления предела числовой
последовательности
сначала необходимо вычислить сумму
числовой последовательности
 функции
функции
 .
.
После находим предел функции с помощью limit().

Рисунок 1 – Вычисление предела числовой последовательности
3.2 Задание №2
Найти пределы нижеперечисленных функций.
а)
 ;
b)
;
b)
 ;
c)
;
c)
 ;
;
d)
 ;
e)
;
e)
 .
.
Для нахождения пределов нижеперечисленных функций необходимо использовать функцию limit().

Рисунок 2 – Вычисление пределов функций
3.3 Задание №3
Используя правила Лопиталя вычислить пределы:
a)
 b)
b)

a) Для вычисления данного предела необходимо просто продифференцировать по отдельности числитель и знаменатель, после найти предел от данной функции.
b)
Для вычисления данного предела необходимо
прежде преобразовать его:
 ,
после вынести экспоненту и найти предел
функции
,
после вынести экспоненту и найти предел
функции
 по правилу Лопиталя.
по правилу Лопиталя.

Рисунок 3 – Задание №3, вычисление предела по Лопиталю

Рисунок 4 – Задание №3 b, вычисление предела по Лопиталю
3.4 Задание №4
Найти производные функций приведенных ниже:
a)
 b)
b)

c)
 d)
d)
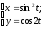
-
Вычисление дифференциала с помощью функции diff() по x
-
Вычисление дифференциала с помощью функции diff() по x
-
Введение функции y зависящей от x, вычисление дифференциала.
-
Введение переменной t, присвоение значений к x и y, вычисление дифференциала.

Рисунок 5 – Вычисление дифференциала «a»

Рисунок 6 – Вычисление дифференциала «b»

Рисунок 7 – Вычисление дифференциала «c»

Рисунок 8 – Вычисление дифференциала «d»
3.5 Задание №5
Вычислить
производную второго порядка функции
 .
.

Рисунок 9 – Вычисление производной второго порядка функции
3.6 Задание №6
Построить график и исследовать функцию на непрерывность, классифицировать точки разрыва:
а)
 б)
б)
 .
.
-
Построение функции
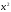 до x
= 3, 2x+1
после 3,
вычисление
пределов функции при x->3,
вследствие их неравенства данная
система функций имеет разрыв первого
рода в точке 3.
до x
= 3, 2x+1
после 3,
вычисление
пределов функции при x->3,
вследствие их неравенства данная
система функций имеет разрыв первого
рода в точке 3.

Рисунок 10 – Построение графика, исследование функции на непрерывность, классифицирование точки разрыва «a»
-
Вычисление пределов функции в точках x = -2 и ч = 2, так как они равны ∞, функция имеет разрыв второго рода в точках -2 и 2.

Рисунок 11 – Построение графика, исследование функции на непрерывность, классифицирование точки разрыва «b»

Рисунок 12 – Результат построения графика, исследования функции на непрерывность, классифицирования точки разрыва «b»
3.7 Задание №7
Построить
график функции
 и
провести полное исследование графика.
и
провести полное исследование графика.

Рисунок 13 – Код программы

Рисунок 14 – Результат программы
3.8 Задание №8
Найти
частные производные функции:
 ,
где
,
где
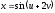 ,
,
 .
.

Рисунок 15 – Нахождение частной производной функции
-
Задание №9
Найти
частные производные функции
 заданной неявно
заданной неявно
 .
.

Рисунок 16 – Нахождение частных производных неявно заданной функции
-
Задание №10
Найти
частную производную указанного порядка
 функции
функции
 .
.

Рисунок 17 – Нахождение частной производной указанного порядка
-
Задание №11
Найти
первый дифференциал функции
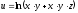 .
.
Для нахождения первого дифференциала необходимо использовать формулу ниже.


Рисунок 18 – Нахождение первого дифференциала функции
-
Задание №12
Найти
экстремумы функции
 .
.
Для нахождения экстремума функции необходимо использовать solve()

Рисунок 19 – Нахождение экстремумов функции
-
Задание №13
Вычислить интегралы:
-
 ;
2.
;
2.
 ;
; -
3.
 ;
4.
;
4.
 ;
;
Для вычисления интегралов используется функция intergral()

Рисунок 20 – Вычисление интегралов
-
Задание №14
Вычислить несобственные интегралы
1)
 ;
2)
;
2) ;
;

Рисунок 21 – Вычисление несобственных интегралов
-
Задание №15
Решить дифференциальные уравнения


Рисунок 22 – Решение первого дифференциального уравнения

Рисунок 23 – Решение второго дифференциального уравнения

Рисунок 24 – Решение третьего дифференциального уравнения

Рисунок 25 – Решение четвертого дифференциального уравнения
 Рисунок
26 – Решение пятого дифференциального
уравнения
Рисунок
26 – Решение пятого дифференциального
уравнения
-
Задание №16
Вычислить площади фигур, ограниченных линиями:
1)
 ;
2)
;
2)
 .
.

Рисунок 27 – Код программы функции №1

Рисунок 28 – Результат программы функции №1

Рисунок 29 – Вычисление площади, ограниченной линиями
-
Задание №17
Вычислить длины кривых:
1)
 ;
2)
;
2)
 .
.
-
Формула нахождения длины кривой в декартовой системе координат:


Рисунок 30 – Вычисление длины кривой
-
Формула нахождения длины кривой в полярной системе координат:


Рисунок 31 – Вычисление длины кривой
-
Задание №18
Найти объем тела, образованного вращением фигуры вокруг
оси ОХ, ограниченной линиями:

Формула
нахождения объема тела, образованного
вращением фигуры вокруг оси ОХ:


Рисунок 32 – Вычисление объема тела, образованного вращением фигуры вокруг оси OX
3.19 Задание №19
Вычислить площадь фигуры, ограниченной линиями:
 .
.
Формула вычисления площади фигуры, ограниченной линиями:


Рисунок 33 – Код программы

Рисунок 34 – Графики функций

Рисунок 35 – Ответ
-
Задание №20
Найти объем тела,
ограниченного конусом:
 и параболоидом:
и параболоидом:
 (Перейти в цилиндрическую систему
координат.)
(Перейти в цилиндрическую систему
координат.)
Исследуем
пересечение двух параболоидов. Поскольку
 ,
то уравнения в цилиндрической системе
записываются в виде:
,
то уравнения в цилиндрической системе
записываются в виде:
 и
и
 ,
тогда существует координата z
= 1. Объем данной области выражается с
помощью тройного интеграла
,
тогда существует координата z
= 1. Объем данной области выражается с
помощью тройного интеграла


Рисунок 36 – Нахождение объема, ограниченного конусом и параболоидом
3.21 Задание №21
Вычислить массу тела, занимающего область

если
 - объемная плотность.
- объемная плотность.
Функция
f(x,y,z)
задает плотность тела
 (x,y,z).
(x,y,z).
M
=
 .
Перейдем
из декартовой в сферическую систему
координат:
.
Перейдем
из декартовой в сферическую систему
координат:



Вследствие
этого получаем
 ;
;
 ;
;


Рисунок 37 – Вычисление массы тела, занимающую область
4 Заключение
В процессе выполнения учебной практики были получены навыки по работе в математическом программном обеспечение SAGE.





