Matan_test (восстановлен)
.docx
Теория вероятностей
-
I:
S: Опыт, эксперимент называется событием
-: Да*
-: Нет
-
I:
S: Вероятность события может быть больше единицы
-: Да
-: Нет*
-
I:
S: В статистическом методе определении вероятности события относительная частота его появления в серии независимых опытов принимается за вероятность этого события
-: Да*
-: Нет
-
I:
S: Вероятность суммы двух несовместимых событий равна сумме их вероятностей
-: Да*
-: Нет
-
I:
S: Сумма вероятностей событий, образующих полную группу, всегда равна единице
-: Да*
-: Нет
-
I:
S: Вероятность произведения двух зависимых событий равна произведению их вероятностей
-: Да
-: Нет*
-
I:
S: Вероятность произведений двух независимых событий равна произведению их вероятностей
-: Да*
-: Нет
-
I:
S: Формула Байеса позволяет вычислять вероятности событий в схеме повторных испытаний
-: Да
-: Нет*
-
I:
S: Дискретная случайная величина в отличие от непрерывной случайной величины принимает только конечное число значений
-: Да*
-: Нет
-
I:
S: Дисперсия случайной величины может принимать как положительные, так и отрицательные значения
-: Да
-: Нет*
-
I:
S: Размерность среднего квадратического отклонения совпадает (в отличие от дисперсии) с размерностью случайной величины
-: Да*
-: Нет
-
I:
S: Различные способы упорядочивания n различных предметов при их расположении слева направо, называются
-: сочетания
-: перестановки*
-: размещения
-
I:
S: Различные способы выбора m предметов из n, отличающиеся самими предметами или порядком их расположения в выборке, называются
-: перестановки
-: размещения*
-: факториал натурального числа n
-: сочетания
-
I:
S: Теория вероятностей изучает
-: массовые закономерности детерминированных событий
-: случайные величины
-: вероятностные закономерности массовых однородных случайных событий*
-
I:
S: Событие - это
-: результат действия 2-х событий
-: исход испытания*
-: сумма событий
-
I:
S: Всякое осуществление комплекса условий, при котором изучается случайное событие, называют
-: вероятность
-: частота
-: испытание*
-
I:
S: Явление, которое может произойти или не произойти при осуществлении некоторого комплекса условий, называется
-: случайное событие*
-: испытание
-: вероятность
-
I:
S: Какие действия над событиями можно производить
-: сложение*
-: деление
-: вычитание
-
I:
S: Событие называется достоверным
-: если при заданном комплексе факторов оно обязательно произойдет*
-: если вероятность его близка к единице
-: если при заданном комплексе факторов оно может произойти
-: если вероятность события не зависит от причин, условий, испытаний
-
I:
S: Событие, которое при заданном комплексе факторов не может осуществиться называется:
-: несовместным
-: независимым
-: противоположным
-: невозможным *
-
I:
S: Будет ли сумма противоположных событий составлять полную группу
-: да*
-: нет
-
I:
S Вероятностью события A называется
-: отношение числа событий, благоприятствующих событию A к числу всех элементарных событий*
-: сумма всех событий, входящих в событие A
-: разность числа элементарных исходов и числа всех событий
-
I:
S: Отношение числа испытаний, в которых событие A появилось, к общему числу испытаний, называют
-: испытание
-: вероятность
-: относительная частота*
-
I:
S: Два события A и B называются независимыми, если:
-: вероятность наступления одного из них зависит от вероятности появления другого
-: вероятность наступления одного из них не зависит от вероятности появления другого*
-: условные вероятности обоих событий равны
-
I:
S: Вероятность произведения двух зависимых событий равна
-: произведению вероятностей первого из них на вероятность второго
-: произведению вероятностей одного из них на вероятность другого, вычисленную при условии, что события независимы
-: произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место*
-: произведению вероятности одного из них на условную вероятность этого события, вычисленную при условии, что второе имело место
-
I:
S: Вероятность произведения двух независимых событий равна
-: произведению вероятности одного из событий на условную вероятность второго
-: произведению вероятности одного из событий на условную вероятность этого же события, при условии, что второе имело место
-: произведению вероятности одного из событий на вероятность второго события*
-
I:
S: Гипотезами называют события, которые
-: являются независимыми и образуют группу
-: являются несовместными
-: являются независимыми
-: являются несовместными и образуют полную группу*
-: образуют полную группу
-
I:
S: Если вероятность наступления события в каждом испытании постоянна, но мала, а число испытаний велико, то для нахождения вероятности того, что событие A произойдет m раз в n испытаниях, следует использовать
-: формулу Бернулли
-: формулу Пуассона*
-: локальную теорему Муавра-Лапласа
-: теорему умножения вероятностей
-
I:
S: В магазин доставили два холодильника, изготовленных на разных заводах. На первом заводе брак составляет 1%, на втором - 2%. Найти вероятность того, что оба холодильника бракованные
-: 0,02
-: 0,002
-: 0,2
-: 0,0002*
-
I:
S: В коробке 9 ампул, из них 4 израсходованных и 5 новых. Наугад вынимают 6 ампул. Какова вероятность того, что среди вынутых ампул будет 2 израсходованные
-: 1/14
-: 2/7
-: 5/14
-: 3/7
-
I:
S: Первый студент из 30 зачетных вопросов выучил 24, второй - 20. Каждому студенту задают по одному вопросу. Какова вероятность того, что хотя бы один студент ответит верно
-: 11/15
-: 14/15*
-: 7/15
-: 13/15
-
I:
S: Сколькими способами можно разложить 5 таблеток по 12 свободным одноместным ячейкам
-: 792
-: 475200
-: 120
-: 95040*
-
I:
S: В поликлинике три кабинета, в которых принимает терапевт. Вероятность того, что каждый терапевт принимает сегодня, равна 0,9. Найти математическое ожидание случайной величины - количества принимающих сегодня терапевтов
-: 2,484
-: 2,652
-: 2,7*
-: 2,9
-
I:
S: Чему равна вероятность достоверного события
-: 1,0*
-: 0,5
-: 0
-: 0,25
-
I:
S: В семье двое детей. Какова вероятность, что старший ребёнок мальчик
-: 1,0
-: 0
-: 0,5*
-: 0,025
-
I:
S: Среди 10 упаковок некоторого препарата 4 упаковки оказалось бракованными. Какова относительная частота бракованного препарата
-: 0
-: 0,4*
-: 0,5
-: 0,6
-
I:
S: Требуется переливание крови. Среди доноров один мужчина и одна женщина. Вероятность, что «нужная» кровь взята у женщины-донора - 0,30, а у мужчины - 0,25. Какова вероятность, что кровь случайно взятого донора окажется «нужной»
-: 0,275*
-: 0,725
-: 0,03
-: 0,5
-
I:
S: Случайная величина, которая принимает отдельные значения из конечного или бесконечного счетного множества, называется
-: дискретная*
-: непрерывная
-: случайная
-
I:
S: Случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка, называют
-: неопределенной
-: относительной
-: непрерывной*
-
I:
S: Вероятность любого отдельного значения непрерывной случайной величины равна
-: 1
-: от 0 до 1
-: близка к нулю
-: 0*
-
I:
S: Математическое ожидание есть
-: среднее арифметическое всех возможных значений случайной величины
-: среднее геометрическое всех возможных значений случайной величины
-: «среднее взвешенное» значение случайной величины*
-
I:
S: В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна
-: 0,15
-: 0,4
-: 0,9
-: 0,45*
-
I:
S: По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,5; при втором - 0,3; при третьем - 0,2; при четвертом - 0,1.
Тогда вероятность того, что мишень не будет поражена ни разу равна
-: 0,003*
-: 1,1
-: 0,275
-: 0,03
-
I:
S: С первого станка на сборку поступает 40%, со второго 60% всех деталей. Среди деталей, поступивших с первого станка 1% бракованных, со второго 2% бракованных. Тогда вероятность того, что поступившая на сборку деталь бракованная, равна
-: 0,014
-: 0,016*
-: 0,015
-: 0,03
-
I:
S: А, В, С -попарно независимые события. Их вероятности: (А)=0,4,Р(В)=0,8,Р(С)=0,3. Укажите соответствие между событиями и их вероятностями:
L1: А*В1
L2: А*С2
L3: В*С3
L4: А*В*С4
R1: 0,32
R2: 0,12
R3: 0,24
R4: 0,096
-
I:
S: Вероятность достоверного события равна
-: -1
-: 0
-: 0,5
-: 1*
-
I:
S: По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,5; при втором - 0,3; при третьем - 0,2; при четвертом - 0,1.
Тогда вероятность того, что мишень не будет поражена ни разу равна
-: 0,003*
-: 1,1
-: 0,275
-: 0,03
-
I:
S: Бросают 2 монеты. События А - "герб на первой монете" и В - "цифра на второй монете" являются:
-: зависимыми
-: совместными*
-: несовместными
-: независимыми*
-
I:
S: В группе 20 студентов. Тогда число способов выбрать среди них старосту и его заместителя, равно
-: 39
-: 210
-: 380*
-: 400
-
I:
S: С первого станка на сборку поступает 40%, со второго 60% всех деталей. Среди деталей, поступивших с первого станка 1% бракованных, со второго 2% бракованных. Тогда вероятность того, что поступившая на сборку деталь бракованная, равна
-: 0,014
-: 0,016*
-: 0,015
-: 0,03
-
I:
S: Число способов выбрать из группы в 20 студентов двух дежурных равно ###
-: 190
-
I:
S: Количество перестановок букв в слове "зачет" равно
-: 20
-: 5
-: 120*
-: 24
-
I:
S: A,B,C-попарно независимые события. Их вероятности: P(A)=0,4;P(B)=0,8;P(C)=0,3
Укажите соответствие между событиями и их вероятностями:
L1: A*B1
L2: A*C2
L3: B*C3
L4: A*B*C4
R1: 0,32
R2: 0,12
R3: 0,24
R4: 0,096
-
I:
S: По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,5; при втором - 0,3; при третьем – 0,2; при четвертом – 0,1.
Тогда вероятность того, что мишень не будет поражена ни разу равна
-: 0,03
-: 0,003*
-: 0,275
-: 1,1
-
I:
S: Какая из формул является формулой Бернулли
-:
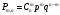 *
*
-:
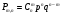
-:
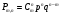
-:
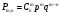
-:
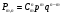
Математическая статистика
-
I:
Q: Установите правильную последовательность действий:
1: сбор статистических данных
2: группировка данных
3: статистическая обработка данных
4: получение практических выводов
-
I:
S: ### называется совокупность случайно отобранных объектов
-: Выборкой
-
I:
S: Если отобранный объект возвращается в генеральную совокупность, то выборка называется ###
-: с возвратом
-
I:
S: Выборка называется ###, если она правильно представляет пропорции генеральной совокупности.
-: репрезентативной
-
I:
S: Мода вариационного ряда 1, 4, 4, 5 ,6, 8, 9 равна
-: 9
-: 5
-: 4*
-: 1
-
I:
S: Проведено 4 измерения (без систематических ошибок) некоторой случайной величины (в мм): 5; 6; 9; 12. Тогда несмещенная оценка математического ожидания равна
-: 8*
-: 8,5
-: 8,25
-: 7
-
I:
S: Точечная оценка математического ожидания нормального распределения равна 10. Тогда ее интервальная оценка может иметь вид
-: (8,6; 9,6)
-: (8,4; 10)
-: (8,5;11,5) *
-: (10; 10,9)
-
I:
S: Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 4; 5; 8; 9; 11. Тогда несмещенная оценка математического ожидания равна
-: 9,25
-: 8
-: 7,7
-: 7,6
-
I:
S: Как называется численное значение признака
-: вариантой *
-: генеральной совокупностью
-: объемом выборки
-: средним значением
-
I:
S: Выборка это
-: ограниченное число элементов, выбранных неслучайно
-: большая совокупность элементов, для которой оцениваются характеристики
-: ограниченное число выбранных случайным образом элементов*
-
I:
S: Статистическим распределением называется
-: перечень вариант или интервалов и соответствующих частот*
-: перечень значений случайной величины или ее интервалов и соответствующих вероятностей
-: перечень вариант или интервалов и соответствующих вероятностей
-: перечень вариант
-
I:
S: Среднее значение выборки является
-: Несмещенной оценкой математического ожидания*
-: Смещенной оценкой математического ожидания
-: Смещенной оценкой дисперсии
-: Несмещенной оценкой дисперсии
-
I:
S: Для того, чтобы по выборке объема n=10 построить доверительный интервал для математического ожидания нормального распределения, нужны таблицы
-: распределения Стьюдента*
-: распределения Пирсона
-: плотности нормального распределения
-: нормального распределения
-
I:
S: Линейная однофакторная модель содержит число коэффициентов, равное
-: 3
-: 4
-: 1
-: 2*
-
I:
S: Математическая статистика является наукой о методах количественного анализа массовых явлений
-: Да*
-: Нет
-
I:
S: Выборочный метод исследования позволяет осуществить целенаправленный отбор объектов, которые более доступны или удобны для исследования
-: Да
-: Нет*
-
I:
S: Репрезентативная выборка - это выборочная совокупность минимального объема
-: Да
-: Нет*
-
I:
S: Вариационный ряд-это упорядоченная последовательность статистических данных
-: Да*
-: Нет
-
I:
S: Для графического изображения статистического распределения используются полигоны и гистограммы
-: Да*
-: Нет
-
I:
S: Медианой называется наиболее часто встречающаяся величина в пределах данного вариационного ряда
-: Да
-: Нет*
-
I:
S: Для количественного определения расхождения между оцениваемым параметром и статистической оценкой пользуются доверительным интервалом
-: Да*
-: Нет
-
I:
S: Гипотезу о виде распределения или о параметрах распределения называют статистической
-: Да*
-: Нет
-
I:
S: При равенстве нулю коэффициента корреляции предполагается, что между х и у существует линейная зависимость
-: Да
-: Нет*
-
I:
S: Количественным показателем тесноты статистической связи х и у является коэффициент корреляции
-: Да*
-: Нет
-
I:
S: Мода вариационного ряда 1,2,2, 3,4,5 равна
-: 17
-: 5
-: 3
-: 2*
-
I:
S: Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 12. Тогда несмещенная оценка математического ожидания равна
-: 8*
-: 7
-: 8,5
-: 8,25
-
I:
S: Точечная оценка математического ожидания нормального распределения равна 10. Тогда её интервальная оценка может иметь вид
-: (8,5;11,5)*
-: (8,4;10)
-: (10;10,9)
-: (8,6;9,6)
-
I:
S: В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 12, Тогда несмещенная оценка дисперсии равна
-: 8
-: 0
-: 3*
-: 4
-
I:
S: Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее
-: увеличится в 5 раз*
-: не изменится
-: увеличится в 25 раз
-: уменьшится в 5 раз
-
I:
S: Мода вариационного ряда 1 , 4 , 4 , 5 , 6 , 8 , 9 равна
-: 9
-: 1
-: 4*
-: 5
-
I:
S: В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 12, 14.
Тогда несмещенная оценка дисперсии равна …
-: 8
-: 0
-: 3
-: 4*
-
I:
S:
Если основная гипотеза имеет вид
![]() ,
то конкурирующей гипотезой может
являться…
,
то конкурирующей гипотезой может
являться…
-:
![]()
-:
![]()
-:
![]() *
*
-:
![]()
-
I:
S: Статистическое распределение выборки имеет вид
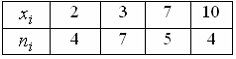
Тогда
относительная частота варианты
![]() ,
равна
,
равна
-: 0,4
-: 4
-: 0,1
-: 0,2*
-
I:
S: Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид
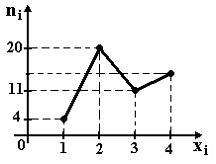
Тогда число вариант xi=4 в выборке равно…
-: 16
-: 50
-: 15*
-: 14
-
I:
S: Из генеральной совокупности извлечена выборка объема n =60, полигон частот которой имеет вид:

Тогда число вариант xi =3 в выборке равно
-: 60
-: 27
-: 25
-: 26*
-
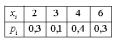
I:
S: В результате 10 опытов получена следующая выборка: 2, 2, 2, 3, 4, 4, 6, 6, 6, 6 Тогда для нее закон распределения будет
-:

-:

-: *
*
-:
-
I:
S: По статистическому распределению выборки

установим ее объем
-: 13*
-: 25
-: 11
-: 30
-
I:
S:
Непрерывная случайная величина X
задана плотностью распределения
вероятностей f(x)=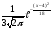 .
Тогда математическое ожидание этой
нормально распределенной случайной
величины равно
.
Тогда математическое ожидание этой
нормально распределенной случайной
величины равно
-: 18
-: 9
-: 3
-: 4*
-
I:
S: По выборке объема n =100 построена гистограмма частот:

Тогда значение а равно
-: 16*
-: 66
-: 15
-: 17
-
I:
S: Из генеральной совокупности извлечена выборка объема n =50:

Тогда n4 равен
-: 23*
-: 250
-: 24
-: 7
-
I:
S:
Статистическое распределение выборки
имеет вид
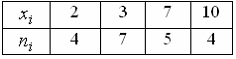 Тогда
относительная частота варианты
Тогда
относительная частота варианты
![]() ,
равна …
,
равна …
-: 0,4
-
I:
S: Дисперсия биноминального распределения вычисляется по формуле
-:
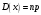
-:
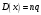
-:
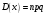 *
*
-:
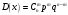
-
I:
S: Нормальное распределение имеет вид
-:
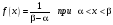
-:
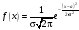 *
*
-:
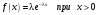
-
I:
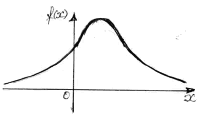
S: Какая из приведенных кривых наиболее точно характеризует график плотности вероятности нормального распределения
|
|
|
|
A |
B |
|
|
|
-: B
-: A*
-: C -: D
-
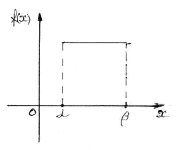
I:
S: Случайная величина распределена равномерно на интервале (10;12) . Тогда ее математическое ожидание и дисперсия соответственно равны …
-:
10,5 и
![]()
-:
10 и
![]()
-:
11 и
![]() *
*
-: 11 и 1