- •Лекционный курс
- •Раздел 1. Линейная алгебра с элементами аналитической геометрии
- •Тема 1. Элементы векторной алгебры и ее приложения.
- •1.1. Линейные операции над векторами
- •1.2. Скалярное произведение векторов
- •1.3. Векторное произведение векторов
- •1.4. Типовые задачи, решаемые средствами векторной алгебры
- •1.5. Линейное, евклидово и нормированное пространства.
- •Тема 2. Матрицы и определители
- •2.1. Понятие матрицы и действия с ними.
- •2.2. Транспонирование матриц
- •2.3. Произведение матриц.
- •2.4. Ранг матрицы
- •2.5. Понятие обратной матрицы
- •2.6.Определители и их свойства.
- •2.7. Линейные операторы и матрицы
- •2.8. Задача о собственных значениях
- •2.9. Свойства симметрических матриц
- •2.10. Квадратичные формы и их приведение к каноническому виду
- •Тема 3. Системы линейных уравнений
- •3.1.Формулы Крамера
- •3.2. Метод Гаусса.
- •3.3.Матричный метод решения линейной системы.
- •3.4. Понятие о приближенных методах решения линейных систем
- •Тема 4. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.
- •4.1. Уравнения линий и поверхностей
- •4.2. Уравнение 1-й степени на плоскости
- •4.3. Уравнения первой степени в пространстве
- •4.4. Уравнения первой степени в пространстве
- •4.5. Типовые задачи на плоскость в пространстве.
- •4.6. Уравнения 2-й степени на плоскости.
- •4.7. Уравнения 2-й степени в пространстве
- •4.8. Цилиндры и поверхности вращения
- •Раздел 2. Математический анализ и дифференциальные уравнения.
- •Тема 5.Функции и их свойства
- •5.1. Функция, способы ее задания, свойства, график функции, преобразование графика сдвигом и деформацией.
- •Тема 6. Пределы и непрерывность.
- •6.1. Понятие предела
- •6.2. Замечательные пределы.
- •6.3. Алгоритм вычисления пределов.
- •6.4. Примеры эквивалентных бмв.
- •Тема 7. Производная и дифференциал функции.
- •7.1. Понятие производной
- •7.2. Дифференциальное исчисление функции одного переменного.
- •7.3. Из определения вытекает алгоритм вычисления производной.
- •7.4.Таблица и основные правила.
- •7.5. Производная и дифференциал.
- •7.6. Производная и дифференциал высшего порядка.
- •Тема 8. Приложения производной
- •8.2.Приложение производной к исследованию функций.
- •Тема 9. Неопределенный интеграл.
- •9.1.Первообразная. Неопределенный интеграл и его свойства
- •9.3.Методы интегрирования.
- •9.4.Рациональные дроби.
- •9.4.Рациональные тригонометрические функции.
- •9.5.Простейшие иррациональные выражения.
- •Тема 10. Определенный интеграл.
- •Методы нахождения определенного интеграла
- •10. 2.Несобственные интегралы.
- •Тема 11. Дифференциальные уравнения.
- •11.1 Определение дифференциального уравнения
- •11.2. Некоторые дифференциальные уравнения первого порядка. Методы Их Решения.
- •Тема 12 Функции нескольких переменных
- •12.1.Основные понятия
- •12.2.Непрерывность функций нескольких переменных
- •12.3.Частные производные и дифференциалы
- •12.4. Производная по направлению и градиент
- •12.5. Производная сложной функции нескольких переменных
- •12.6. Производные и дифференциалы высших порядков
- •12.7. Производные неявных функций
- •12.8.Экстремумы функций нескольких переменных
- •Раздел 3. Ряды.
- •Тема 13. Числовые и степенные ряды.
- •Раздел 4. Теория вероятностей и математическая статистика
- •Тема 14. Основные понятия теории вероятностей.
- •1. Понятие события.
- •2. Классическое определение вероятности. Свойства вероятности.
- •3. Статистическое определение вероятности.
- •4. Элементы комбинаторики
- •Тема 15. Основные теоремы теории вероятностей и следствия из них.
- •15.1.Теорема сложения.
- •15.2. Условная вероятность события. Теорема умножения
- •15.3. Вероятность появления хотя бы одного события
- •15.4. Формула полной вероятности.Формула Байеса.
- •15.5. Повторные независимые испытания
- •15.6. Локальная теорема Муавра- Лапласа
- •15.7. Интегральная теорема Муавра-Лапласа.
- •Тема 16. Случайные величины и способы их описания
- •16.1. Понятие случайной величины. Дискретные и непрерывные
- •16.2. Функция распределения случайной величины. График функции
- •16.4. Равномерный закон распределения.
- •16.6. Правило «трех сигм».
- •16.7. Показательное распределение.
- •16.8. Функция надежности.
- •16.9. Показательный закон надежности.
- •16.10. Математическое ожидание.
- •16.11. Дисперсия.
- •16.12. Числовые характеристики непрерывных случайных величин.
- •16.13. Числовые характеристики случайных величин, имеющих некоторые стандартные законы распределения.
- •1. Биномиальное распределение.
- •2. Закон Пуассона.
- •3. Равномерное распределение.
- •4. Нормальное распределение.
- •16.14. Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли.
- •Корреляционный анализ.
- •Глоссарий
- •Темы контрольных работ.
- •Основная литература
- •Дополнительная литература
2.9. Свойства симметрических матриц
Определение. Матрицу называют симметрической, если aij=aji. Для всех i,j.
Теорема. Собственные значения симметрической матрицы – действительные числа, собственные векторы – ортогональны.
Доказательство.
Ограничимся матрицей размерности 2.
Имеем А= .
.
Характеристическое
уравнение имеет вид к2-(а11+а22)+(а11а22-а122)=0.
Его дискриминант равен
(а11+а22)2-4(а11а22-а122)=
(а11-а22)2+4а122![]() 0.
А это значит – корни квадратного
уравнения действительные числа.
0.
А это значит – корни квадратного
уравнения действительные числа.
Рассмотрим
случай разных корней . Тогда по Виету
имеем к1+к2=
а11+а22,
и к1к2=
а11а22-а122
.С
другой стороны для к1
найдем собственный вектор
![]() 1
из системы
1
из системы

Как
известно, в этой системе одно из уравнений
лишнее, т.к. r(A)=1.
И потому мы отбросим , например, второе
уравнение в системе и возьмем х2=а11-к1
. Тогда получим собственный вектор
![]() 1=(-а12
а11-к1)T
. Из аналогичных рассуждений найдем
1=(-а12
а11-к1)T
. Из аналогичных рассуждений найдем
![]() 2=(-а12
а11-к2)T
. Теперь вычислим их скалярное произведение
2=(-а12
а11-к2)T
. Теперь вычислим их скалярное произведение
![]() 1
1![]() 2=а122+(а11-к1)(а11-к2)=
а122+а112-
а11(а11+
а22)+
а11а22-а122
=0.
2=а122+(а11-к1)(а11-к2)=
а122+а112-
а11(а11+
а22)+
а11а22-а122
=0.
Если
же корни равны, то это происходит только
тогда, когда одновременно а12=0
и а11-
а22=0.
Но это может быть только если к1=
к2
= а11.
Но тогда в качестве
![]() 1
можно взять
1
можно взять
![]() 1=(1
0)T
,а в качестве
1=(1
0)T
,а в качестве
![]() 2
можно взять
2
можно взять
![]() 2=(0
1)T
.
И все равно они будут ортогональны.
2=(0
1)T
.
И все равно они будут ортогональны.
2.10. Квадратичные формы и их приведение к каноническому виду
Пусть
в ЛП размерности 2 задан
![]() =(
х1 х2)T в нормированном евклидовом
ортогональном базисе i,j.
=(
х1 х2)T в нормированном евклидовом
ортогональном базисе i,j.
Определение.
Выражение ф(х1,х2)= а11х12+2а12 х1 х2 +а22х22=0
где aij - действительные числа, называют
квадратичной формой двух переменных
х1,х2. Ее можно записать иначе ф(х1,х2)=
(а11х1+а12х2) х2+(а12 х1+а22х2)х2. Затем, используя
умножение матрицы на вектор получить
ф(х1,х2)=
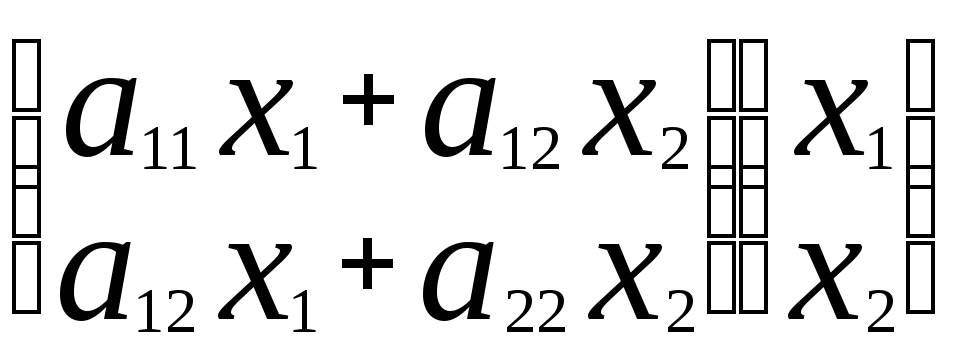 =((
=((
![]() ),
),![]() )=(Ах,х), причем матрица А – симметрическая
и , как известно, ее собственные векторы
ортогональны. Пусть это будут векторы
)=(Ах,х), причем матрица А – симметрическая
и , как известно, ее собственные векторы
ортогональны. Пусть это будут векторы
![]() 1
и
1
и
![]() 2
. Тогда их можно нормировать и принять
в качестве базисных в ортонормированном
евклидовом ЛП. Построим единичные
векторы в новом базисе (базисе собственных
векторов матрицы А). Получаем
2
. Тогда их можно нормировать и принять
в качестве базисных в ортонормированном
евклидовом ЛП. Построим единичные
векторы в новом базисе (базисе собственных
векторов матрицы А). Получаем
![]() и
и![]() - новые единичные . И в этом новом базисе
вектор
- новые единичные . И в этом новом базисе
вектор
![]() =(
х’1 х’2)T. Но в этом случае и квадратичная
форма примет новый вид ф(х1,х2)= (А(х’1
=(
х’1 х’2)T. Но в этом случае и квадратичная
форма примет новый вид ф(х1,х2)= (А(х’1![]() +
х’2
+
х’2![]() ),
х’1
),
х’1![]() +
х’2
+
х’2![]() ).
Но т.к.
).
Но т.к.![]() и
и![]() - собственные для А, то получаем ф(х1,х2)=(
(х’1 к1
- собственные для А, то получаем ф(х1,х2)=(
(х’1 к1![]() +
х’2 к2
+
х’2 к2![]() ),
х’1
),
х’1![]() +
х’2
+
х’2![]() )=
к1(х’1)2+ к2(х’2)2 . Получен новый вид
квадратичной формы, в котором отсутствует
произведение текущих координат. Такой
вид носит название – канонического
вида квадратичной формы.
)=
к1(х’1)2+ к2(х’2)2 . Получен новый вид
квадратичной формы, в котором отсутствует
произведение текущих координат. Такой
вид носит название – канонического
вида квадратичной формы.
Т.о. в декартовом базисе собственных нормированных векторов матрицы квадратичной формы сама форма принимает канонический вид.
Остается
важная задача: установить связь между
координатами вектора
![]() =(
х1 х2)T начального базиса i,j и координатами
того же вектора
=(
х1 х2)T начального базиса i,j и координатами
того же вектора
![]() =(
х’1 х’2)T в новом базисе нормированных
собственных векторов матрицы квадратичной
формы.
=(
х’1 х’2)T в новом базисе нормированных
собственных векторов матрицы квадратичной
формы.
Мы
имеем
![]() =
х1i+х2j = х’1I+х’2J . Но I и J тоже векторы,
правда единичной длины. И потому I=iCos
=
х1i+х2j = х’1I+х’2J . Но I и J тоже векторы,
правда единичной длины. И потому I=iCos![]() +jCos(90-
+jCos(90-![]() ),
J= iCos
),
J= iCos![]() +jCos(90+
+jCos(90+![]() ).
Или после подстановки полученного
вместо координат х’1,х’2 получим связь
между старыми и новыми координатами
).
Или после подстановки полученного
вместо координат х’1,х’2 получим связь
между старыми и новыми координатами
![]() =
=![]() (
х’1 х’2)T, которая соответствует матрице
поворота плоскости на некоторый угол.
(
х’1 х’2)T, которая соответствует матрице
поворота плоскости на некоторый угол.

Контрольные вопросы и задания для самостоятельной подготовки:
Понятие матрицы.
Линейные операции над матрицами.
Транспонирование матриц.
Произведение матриц.
Собственные значения и собственные векторы матриц.
Ранг матрицы.
Понятие обратной матрицы.
Операции над определителями.
Свойства определителей.
Миноры и алгебраические дополнения.
Линейные операторы.
Собственные векторы и собственные значения линейного оператора.
Понятие квадратичной формы.
Преобразование квадратичной формы при замене переменных.
Приведение квадратичной формы к каноническому виду.
Метод Лагранжа.
Закон инерции квадратичных форм.
Положительно определенные квадратичные формы. Критерий Сильвестра
Найти произведение матриц
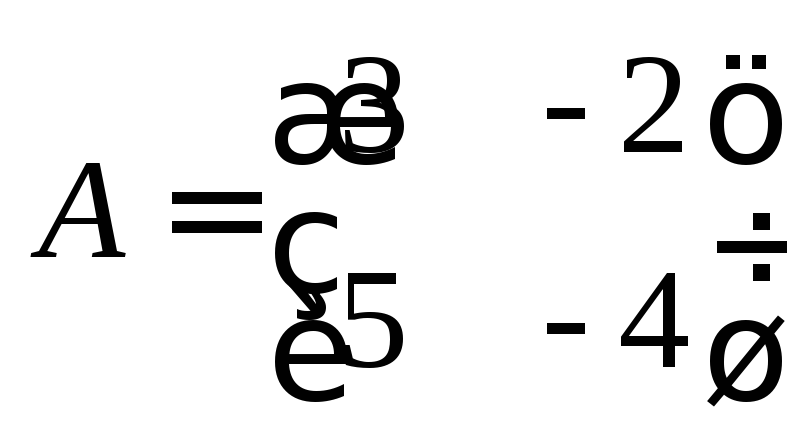

Найти матрицу С= -5А - 2В: А =
 В=
В=
Найти матрицу
 ,
если
,
если
Найти обратную матрицу
 ,
если
,
если

Вычислить определитель матрицы

Найти матрицу
 ,
если
,
если
Найти обратную матрицу
 ,если
,если
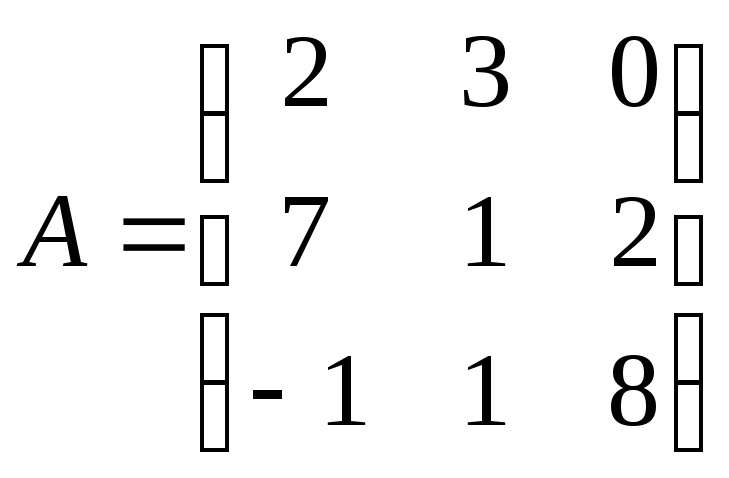
Вычислить определитель матрицы

Найти матрицу
 ,
если
,
если
Найти обратную матрицу
 ,
если
,
если

Вычислить определитель

Найти матрицу
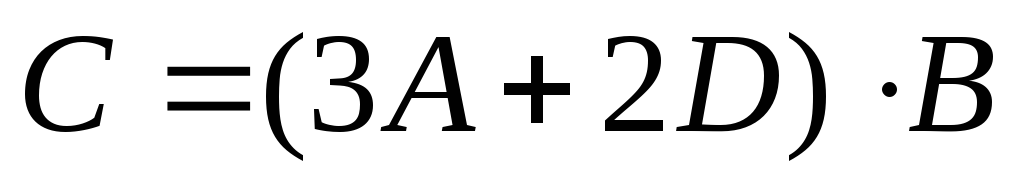 ,
если
,
если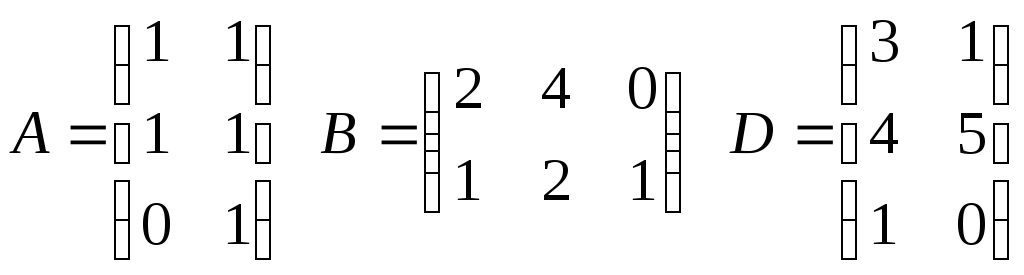
Найти обратную матрицу
 ,
если
,
если

Вычислить определитель

Вычислить определитель матрицы четвертого порядка:

Найти матрицу, обратную данной: А =

Найти ранг матрицы: