3.2. Метод Гаусса.

Следует отметить, что метод Крамера является очень трудоемким по количеству вычислений и требует порядка арифметических действий для нахождения решения системы линейных уравнений. Приэто составит около 3000 действий. При решении серьезных задач приходится иметь дело с системами уравнений порядкаи более. При таких масштабах даже суперкомпьютерам потребуется огромное время для вычисления решения. Кроме того, погрешности компьютерного округления чисел приводят к значительным ошибкам в расчетах численного решения систем уравнений большего порядка. Между тем существует более экономичный способ решения систем линейных уравнений, основанные на предварительном преобразовании расширенной матрицы системы к специальному виду. В частности, одним из них является метод Гаусса.

Рассмотрим систему линейных уравнений общего вида (1). Пусть для определенности (если, то можно переставить на первое место ненулевое слагаемое или начать с другого уравнения). Умножим первое уравнение системы (1) на числои затем вычтем его из второго уравнения этой системы. Умножим обе части первого уравнения на числои затем вычтем его из третьего уравнения и так далее, т.е. процесс заключается в последовательном вычитании первого уравнения, умножаемого на числа, изуравнения. Таким образом, в результате элементарных преобразований мы получим эквивалентную систему, в которой начиная со второго уравнения отсутствуют слагаемые, содержащие неизвестное:

где верхний индекс в скобках означает новые коэффициенты, полученные после первого шага. Для удобства записи будем оперировать расширенной матрицей системы, отделяя в ней вертикальной чертой столбец свободных членов. Итак, после первого шага, содержащего элементарных преобразований системы, мы переходим от расширенной матрицы (1.4) исходной системы к расширенной матрице

.

Второй шаг заключается в том, что теперь второе уравнение системы или вторая строка матрицы используется для аналогичных элементарных преобразований строк с третьей по: эта строка последовательно умножается на числои вычитается изстроки. В результате этихэлементарных преобразований получаем новую расширенную матрицу, соответствующую новой эквивалентной системе уравнений. Эта матрица имеет вид

,

где верхний индекс означает новые коэффициенты. В случае если элемент то второе уравнение можно поменять местами с другим уравнением, у которого элемент

Продолжаем этот процесс аналогичным образом до тех пор, пока не дойдем до последней - строки. После-го шага процесса последовательного исключения неизвестных мы получим следующую расширенную матрицу:

.

Последние строк этой матрицы соответствуют уравнениям эквивалентной системы уравнений

;

Эти уравнения могут появляться, если соответствующие уравнения исходной системы (1) представляют собой линейные комбинации других уравнений этой системы. Таким образом метод Гаусса, позволяет на определенном шаге установить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся линейными комбинациями других уравнений системы (1), если она совместна.

Пусть система (1) совместна, тогда все правые части уравнений (2) равны нулю, и после удаления нулевых уравнений в эквивалентной системе и нулевых строк в расширенной матрице получаем матрицу специфического ступенчатого вида, ранг которой равен r. Все элементы этой матрицы, стоящие слева или ниже элементов, равны нулю:

Эта расширенная матрица соответствует системе уравнений ранга, которая имеет вид:

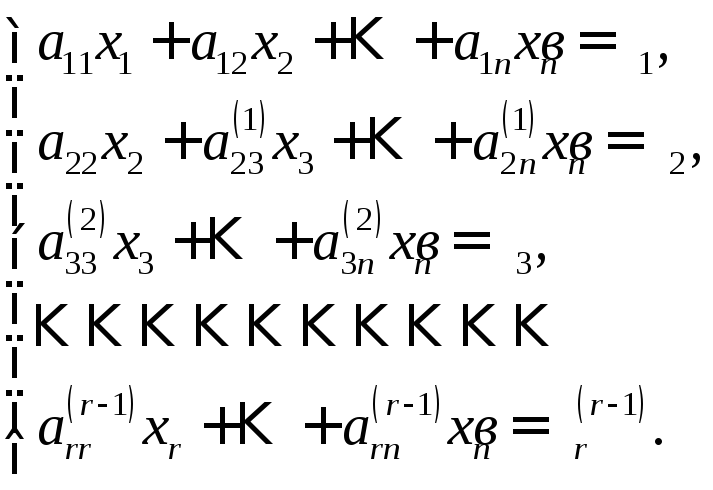
Система уравнений (4) уже полностью подготовлена к нахождению решения, процесс которого осуществляется снизу вверх, т.е. от последнего уравнения к первому. Переход от системы (1.1) к эквивалентной ей системе (4) называется прямым ходом, а нахождение неизвестных из системы (4) обратным ходом метода Гаусса. Далее последовательность действий аналогична изложенной выше.

Пример. Решить систему линейных уравнений методом Гаусса.

Решение. Составим расширенную матрицу этой системы, после чего выполним соответствующие преобразования методом Гаусса. Имеем

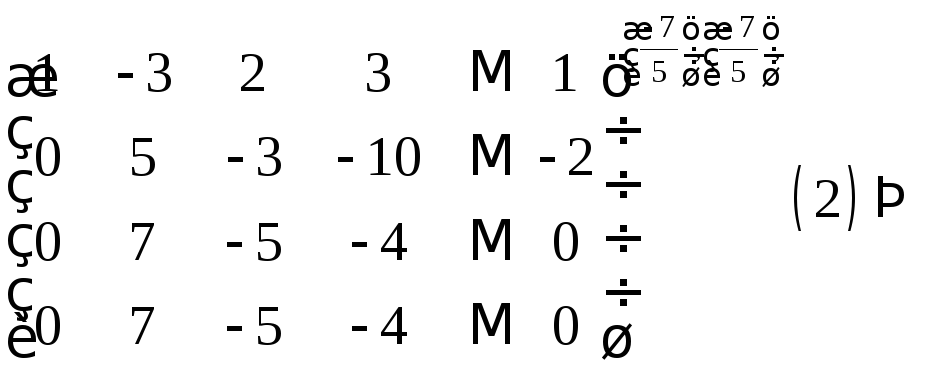
Последняя нулевая строка в расширенной матрице, полученной после 3-го шага, появилась из-за того, что в исходной системе четвертого уравнения является суммой 1-го и 3-го уравнений. Система совместна , и после удаления нулевой строки заключительный вид расширенной матрицы соответствует системе трех уравнений с четырьмя неизвестными (ранг системы меньше числа неизвестных). Полагая свободной переменной, получаем

Из этой системы обратным ходом метода Гаусса находим

, ,.

Данная система уравнений имеет бесконечное множество решений, поскольку может принимать любые значения.