Содержание

Глава 1. Критерий совместимости……………………………………………….3

Глава 2. Метод Гаусса…………………………………………………………….5

Глава 3. Формулы Крамера………………………………………..……………11

Глава 4. Матричный метод……………………………………………………...14

Список литературы………………………………………………………………15

Глава 1

Критерий совместимости

Система линейных уравнений имеет вид:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂ (5.1)

……………………………..

a_m1x₂ + a_m2x₂ +... + a_mnx_n = b_m

Здесь а_ij и b_i (i = ; j = ) - заданные, а x_j - неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:

AX = B, (5.1)

где A = (а_ij) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы, X = (x₁, x₂,..., x_n)^T, B = (b₁, b₂,..., b_m)^T - векторы-столбцы, составленные соответственно из неизвестных x_j и из свободных членов b_i..

Упорядоченная совокупность n вещественных чисел (c₁, c₂,..., c_n) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x₁, x₂,..., x_n каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c₁, c₂,..., c_n)^T такой, что AC ≡ B.

Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Матрица

à =

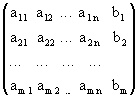
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы (5.1) решается следующей теоремой.

Теорема Кронекера- Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и Ã совпадают, т.е.

r(A) = r(Ã) = r

Для множества М решений системы (5.1) имеются три возможности:

1. M = Ø (в этом случае система несовместна);

2. M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);

3. M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.

Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m ≥ n); если m > n, то m-n уравнений являются следствиями остальных. Если 0 < r < n, то система является неопределенной.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂ (5.3)

………………………………

a_n1x₂ + a_n2x₂ + ... + a_nnx_n = b_n

Системы (5.3) решаются одним из следующих способов:

1. методом Гаусса, или методом исключения неизвестных;

2. по формулам Крамера;

3. матричным методом.

Глава 2

Метод Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Возвратимся матрицам. Рассмотрим теперь прямоугольную матрицу,

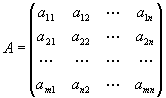
имеющую m строк и n столбцов. Ее называют матрица размером m на n. А(mхn). Выделим в этой матрице произвольные к строк и к столбцов. Они образуют квадратную матрицу B(kхk)

Например:

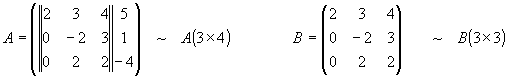
Минором К-ого порядка матрицы А называется определитель квадратной матрицы, получающейся из данной матрицы выделением произвольных к строк и к столбцов.

½ B½ =detB- является минором третьего порядка.

Минором второго порядка является, например определитель

Сами элементы матрицы можно рассматривать как миноры первого порядка. Какие-то из миноров равны нулю, какие-то нет. Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля. Если ранг А обозначаемый r (A) равен r, то это означает, что в А имеется хотя бы один отличный от нуля минор порядка r, но всякий минор, порядка больше чем r, равен нулю.

Например, найдем ранг матрицы

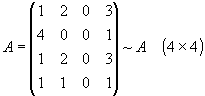
1. Проверяем минор 4 порядка ½ A½ =0, т.к. матрица содержит нулевой столбец.

2. Проверяем миноры 3 порядка

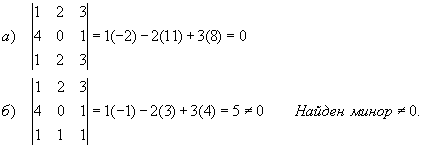
Итак, процесс вычислений миноров прекращаем, поскольку миноров 4 порядка, не равных нулю нет, а минор 3-го порядка найден. Значит r(A)=3.

Мы уже рассматривали методы решения систем линейных алгебраических уравнений, но только в тех случаях, когда матрица системы – квадратная, то есть число уравнений равно числу неизвестных. Рассмотрим теперь самый простой и употребительный способ решения систем линейных уравнений – метод Гаусса. Рассмотрим его на простейшем примере, решая систему трех уравнений с тремя неизвестными.

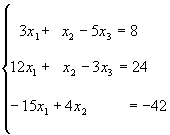
Мы хотим исключить х₁ из всех уравнений, кроме первого. Для этого мы должны вычесть из второго уравнения первое, умноженное на 4, а к третьему прибавить первое, умноженное на 5.

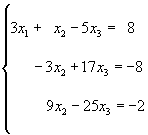
На втором шаге исключения мы не трогаем первое уравнение. Другие два уравнения содержат два неизвестных х₂ и х₃ и к ним можно применить ту же процедуру исключения. Для этого к третьему уравнению прибавляем второе, умноженное на 3.

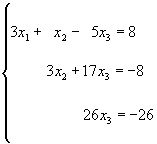
Далее наши действия очевидны. Из третьего уравнения х₃=-1, подставляя это значение во второе уравнение, получаем х₂=-3 и наконец, из первого уравнения получаем х₁=2. Этот простой процесс называется простой подстановкой. Таким образом, процесс решения системы линейных алгебраических уравнений по методу Гаусса состоит из двух этапов.

Первый этап (прямой ход метода) – система приводится к треугольному виду.

Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым.

Аналогично, эту идею последовательного исключения можно применить и в случае матрицы А(mxm) размера больше 3х3.

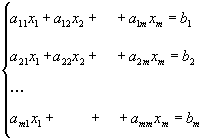
Без ограничения общности можно считать, что в нашей системе ведущий элемент a₁₁0 первого шага (иначе просто переставим уравнение). На первом шаге мы просто исключим х₁ из всех уравнений, начиная со второго, для чего из второго уравнения почленно вычтем первое, умноженное на а₂₁/а₁₁, из третьего почленно вычтем первое, помноженное на а₃₁/а₁₁ и т.д.. Тогда система заменится эквивалентной системой:

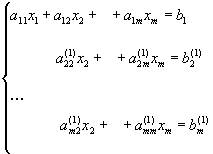
Коэффициенты при неизвестных и свободные члены в последних m-1 уравнениях системы, определяются формулами:

Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a₁₁0

На втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а₂₂⁽¹⁾ (если a₂₂⁽¹⁾0)

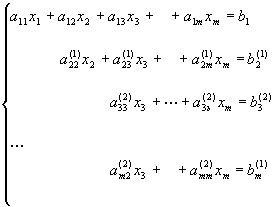
Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.

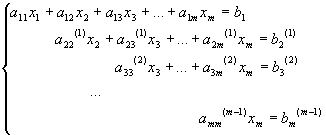
Матрица этой системы имеет вид:

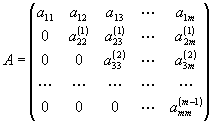
На этом прямой ход метода Гаусса заканчивается. Второй этап – обратный ход, заключается в решении треугольной системы. Из последнего уравнения находим x_m. По найденному x_m из (m-1) уравнения находим x_m-1. Затем по x_m-1 и x_m из (m-2) уравнения находим x_m-2. Процесс продолжаем, пока не найдем x₁ из первого уравнения.

Если у нас число уравнений меньше числа неизвестных, то мы придем не к треугольной системе, а к ступенчатой.

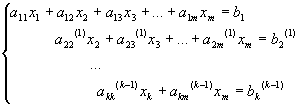
Так как прямой ход метода Гаусса прервется, когда уравнения закончатся, а неизвестные еще останутся. В таком случае в каждом уравнении системы перенесем все члены с неизвестными x_k+1,….,x_m в правую часть.

Придавая неизвестным x_k+1,….,x_m (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными). Так как произвольные значения можно придавать любыми способами, система будет иметь бесчисленное множество значений.

В решении следующего примера не будем выписывать каждую систему, а ограничимся лишь преобразованиями над матрицами:

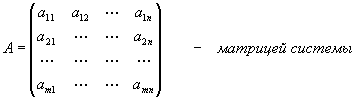
и

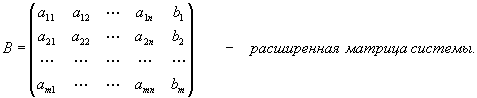
Такая модификация метода называется методом Жордана-Гауcса.