Лекция 3

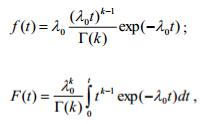
Гамма-распределение (γ-распределение) случайной величины используется для характеристики времени возникновения отказов сложных электротехнических систем на начальной стадии эксплуатации, т.е. в период их приработки, а также при исследовании надежности объектов с резервированными элементами. При этом рассматриваются события отказа объекта после k отказов элементов, подчиняющихся экспоненциальному закону распределения с интенсивностью λ0 .

Характеристики гамма-распределения:

(3.27)

(3.28)

где λ0 и k – параметры гамма-распределения; Г(k) = (k -1)! – гаммафункция.

Распределение Вейбулла – распределение промежуточное между нормальным и экспоненциальным. Оно удобно для подбора наиболее подходящего выражения по результатам эксперимента. Наблюдается при отказах некоторых механических узлов, например, шарикоподшипников; при отказах электрической изоляции, инициируемых постепенным накоплением дефектов; при отказах некоторых электрических элементов в период приработки и в режимах ускоренных испытаний на надежность, т.е. когда

В начало лекции

3.5. Понятие и характеристики случайных процессов

Если случайная величина изменяется в процессе опыта в связи с изменением некоторых факторов, то ее можно характеризовать случайной функцией, т.е. такой функцией, которая в результате опыта принимает тотили иной вид, неизвестный заранее. Конкретный вид, принимаемый случайной функцией при проведении опыта, называется ее реализацией.

Случайная функция, аргументом которой является время, называется случайным, или вероятностным процессом.

Понятие «поток событий» и «процесс» взаимосвязаны. Например, процесс изменения состояния объекта вызывается потоками отказов и восстановлений. Более того, в некоторых литературных источниках эти понятия рассматриваются как идентичные.

Рассмотрим некоторый случайный процесс (случайную функцию) X(t). Предположим, что в результате проведения n независимых опытов получено n ее реализаций (рис. 3.5). Обозначим их соответственно номеру опыта как x1(t),x2(t),...,xn (t). Каждая из этих реализаций является обычной (неслучайной) функцией времени.

Зафиксируем некоторое значение аргумента, например, t = t j . При этом получим n численных значений x1(t j ),x2(t j ),...,xn(t j ) случайной величины X(t j ) в момент времени t j .

Используя m подобных сечений по оси t, можно с некоторым приближением заменить рассмотрение случайной функции рассмотрением системы m случайных величин: X(t1), X(t2),..., X(tm) . По мере увеличения числа таких сечений подобная замена дает все большую точность. В пределе при бесконечно большом числе сечений можно получить полностью адекватное описание случайной функции. Таким образом, понятие случайной функции можно рассматривать как обобщенное понятие системы случайных величин. Следовательно, к случайной функции применимо такое понятие, как закон

распределения. Однако его выражение в виде функции бесконечного множества аргументов практически невозможно.

При решении задач надежности и диагностики используют вероятностные характеристики, аналогичные рассмотренным законам распределения случайных величин, но для определенных временных сечений. Эти характеристики в общем случае зависят от места сечения, т.е. от значения t, и выражаются как F(x,t) . Функция такого вида называется одномерной функцией распределения случайной функции X(t) и выражает одномерный закон распределения.

Обычно рассматривают отдельные свойства случайных функций, для описания которых используют простейшие характеристики, аналогичные числовым характеристикам случайных величин, такие как математическое ожидание, дисперсия и среднеквадратическое отклонение, рассчитываемые для различных моментов времени.

Рисунок 3.4 - Пример реализации случайного процесса В отличие от числовых характеристик случайных величин,

представляющих собой определенные числовые значения, характеристики случайных функций в общем случае представляют собой не числа, а функции времени, причем неслучайные.

Математическим ожиданием случайной функции X(t) называется неслучайная функция M x (t) , которая при каждом значении аргумента t равна математическому ожиданию случайной величины в соответствующем

сечении случайной функции. Она представляет собой некоторую среднюю функцию, около которой варьируются все возможные реализации случайного процесса.

Дисперсией случайной функции X(t) называется неслучайная функция Dx (t), значение которой для каждого t равно дисперсии случайной величины в этом сечении.

В соответствии с этими определениями M x (t) и Dx (t) могут быть рассчитаны по формулам, рассмотренным в 3.3.

Среднее квадратическое отклонение случайной функции

(3.31)

Если аргумент t принимает лишь дискретные значения, функцию X(t) называют случайным процессом с дискретным временем (случайная последовательность событий), если же t изменяется на некотором интервале, то X(t) – случайный процесс с непрерывным временем.

Всвою очередь, если случайные величины из совокупности, образующей X(t), принимают дискретные значения, то имеет место процесс с дискретными случайнымизначениями,если же непрерывные – тоимеет место процесс с непрерывными случайными значениями.

Вначало лекции

3.6. Марковские случайные процессы

В теории надежности и технической диагностике наибольшее распространение получили пуассоновские потоки таких событий, как отказы, восстановления, неплановые простои, переводы в режим диагностирования и пр. Все они характеризуют изменения состояния объекта в процессе его использования и представляют собой вероятностныепроцессы с дискретными значениями реализуемых состояний при отсутствии последействия. Такого вида процессы относятся к классу марковских случайных процессов.

Марковскимпроцессом называют такойслучайныйпроцесс, укоторого для каждого момента времени вероятность любого состояния объекта в будущем зависит только от его состояния в настоящий момент времени и не зависит от того, каким образом объект пришел в это состояние. При этом обязательным условием является экспоненциальное распределение времени нахождения объекта в каждом из возможных состояний.

Марковские процессы с дискретным временем, для которых разности смежных моментов наблюдения ti -ti-1 принимаются одинаковыми, равными постоянной величине t – шагу, а вероятности перехода из состояния в состояние зависят лишь от величины шага и не зависят от того, где на оси времени происходит переход, называются однородными марковскими процессами (ОМП), или цепями Маркова.

ОМПможетбытьпроиллюстрированвременнойдиаграммойпереходов, представляющей собой возможную реализацию процесса, или графом состояний, как показано на рис. 3.5 для случая трех возможных состояний:

S1,S2 и S3 .

Шаги по оси времени приняты в относительных единицах t* = t / t. Вершины графа представляют собой вероятности состояний Рi, а

операторы ветвей – интенсивности переходов qi, j . Возможно также представление ОМП матрицей вероятностей переходов. Для графа, изображенного на рис. 3.5,б, такая матрица имеет вид

Временной процесс перехода из состояния в состояние можно представить также способом, несколько отличающимся от рассмотренного выше. При этом возможные переходы происходят не в конце каждого дискретногошага,аспустянекотороеслучайноевремяτi, j пребыванияобъекта в предыдущем состоянии Si перед переходом в последующее S j . Процесс,

рассматриваемый в такой интерпретации, называют неоднородным марковским, или полумарковским.

Рисунок 3.5 - Способы представления ОМП: а – временная диаграмма переходов; б – граф состояний

В теории надежности и технической диагностике рассматривают в основном стационарные марковские процессы, т.е. такие процессы, у которых вероятности нахождения объекта в возможных состояниях остаются неизменными во времени. Значения этих вероятностей могут быть получены в результате решения системы алгебраическихуравнений,описывающихграф состояний.

Уравнения составляют по правилу, заключающемуся в том, что алгебраическая сумма входящих и выходящих сигналов для каждой вершины графа равна нулю. Сигналы представляют собой произведения вероятностей состояния на оператор выходящей ветви. При этом входящие в вершину сигналы берут со знаком «плюс», а выходящие – со знаком «минус». К полученной таким способом системе добавляют уравнение

где n – число вершин графа.

В начало лекции

Контрольные вопросы

1. Какие события называются случайными?

2.Какой поток случайных событий считается простейшим?

3.Понятие и виды случайных величин.

4.Что представляет собой функция распределения случайной величины?

5.Математические и статистические оценки числовых характеристик случайных величин.

6.Назовите три типовые периода эксплуатации, характерные для любого технического изделия.

7.Основные виды законов распределения случайных величин и событий. Области их применения. Понятие и характеристики случайного процесса.

Вначало лекции