Питання до колоквіуму з фізики за другий модуль

1. Електричне поле. Закон Кулона в векторному вигляді. Принцип суперпозиції.

Електростатика - це розділ фізики, що займається вивченням властивостей та взаємодією нерухомих зарядів.

Навколо кожного електричного заряду існує електричне поле - особливий вид матерії, що існує незалежно від наших знань про нього і має енергію. Електричне поле неперервне в просторі і здатне діяти на інші електричні заряди.

Силовою характеристикою електричного поля є фізична величина, яка називається напруженістю. Поле, яке існує навколо електричних зарядів досліджують з допомогою пробного заряду. Під пробним зарядом розуміють малий додатній заряд, який своїм полем не може спотворювати досліджуване поле, отже це уявний заряд, власне електричне поле якого досить слабке порівняно з досліджуваним.

Принцип суперпозиції – один із найзагальніших законів у багатьох розділах фізики. Найпростіше формулювання принципу суперпозиції звучить так: результат впливу на частинку кількох зовнішніх сил є просто сума результатів впливу кожної із сил.

Найбільш відомий принцип суперпозиції в електростатиці, в якій він стверджує, що електростатичний потенціал, який створюється в даній точці системою зарядів, є сума потенціалів окремих зарядів.

Електростатична сила взаємодії F12 двох точкових нерухомих зарядів q1 та q2 у вакуумі прямо пропорційна добутку абсолютних значень зарядів і обернено пропорційна квадрату відстані r12 між ними.

Сила взаємодії направлена вздовж прямої, що з'єднує заряди, причому однойменні заряди відштовхуються, а різнойменні притягуються. Сили, що визначаються законом Кулона адитивні.

Для виконання сформульованого закону необхідно, щоб виконувалися такі умови:

1.Точковість зарядів — відстань між зарядженими тілами має бути набагато більшою від розмірів тіл.

2.Нерухомість зарядів. У протилежному випадку потрібно враховувати магнітне поле заряду, що рухається[1].

3.Закон сформульовано для зарядів у вакуумі.

,

2. Теорема Гауса і її застосування для розрахунку поля точкового заряду (Площини, двох паралельних площин, сфери, кола і циліндра).

1. Напруженість поля, створювана нескінченно протяжної однорідно зарядженої площини з поверхневою густиною заряду σ. ПОВЕРХНЕВА ГУСТИНА ЗАРЯДУ показує, який заряд припадає на одиницю площі

Лінії напруженості перпендикулярні розглянутої поверхні й спрямовані від неї в обидва боки. Побудуємо циліндр із основоюS, твірна якого паралельна лініям напруженості .

 

 

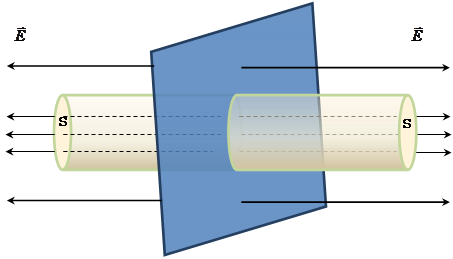Тому що твірна  циліндра паралельна, то потік через основуS рівний

Потік через бічну поверхню циліндра дорівнює нулю, тому що перпендикулярнаS cosα= cos90° = 0, отже,

2. Напруженість поля, створювана двома паралельними нескінченно протяжними пластинами з поверхневою густиною зарядів +σ і -σ. Знайдемо поле Е, використовуючи принцип суперпозиції  полів. В області між площинами

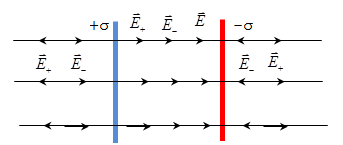
Ліворуч і праворуч від площин поля віднімаються, тому що лінії напруженості спрямовані назустріч одна одній .

 

3. Напруженість поля, створювана нескінченно протяжною  ниткою з лінійною густиною заряду а τ.

Лінійна густина заряду       показує,         який заряд припадає на одиницю довжина провідника.

 

Потрібно визначити напруженість поля на деякій відстані r від нитки. Для цього побудуємо циліндр радіуса r і висотою h, по осі якого проходить нитка.

Потік через основи розглянутого циліндра дорівнює нулю, тому що перпендикулярна вектору, отже, потік буде визначатися тільки потоком через бічну поверхню циліндра