На колоквіум з вишки (Ряди)

На колоквіум з вишки (Ряди) 1

Q9.1. Що називається числовим рядом? 1

Q9.2. Часткова сума ряду визначається рівністю 2

Q9.3. Який ряд називається збіжним? Що називається сумою ряду? 2

Q9.4. У чому полягає необхідна умова збіжності ряду? 3

Q9.5. У чому полягає основна (перша) ознака порівняння рядів з додатними членами? 3

Q9.6. У чому полягає гранична (друга) ознака порівняння рядів з додатними членами? 4

Q9.7. У чому полягає інтегральна ознака збіжності або роз­біж­ності ряду з додатними членами ? Яка оцінка справедлива для суми цього ряду? 5

Q9.8. Згідно з інтегральною ознакою для суми збіжного ряду справедлива наступна оцінка. 6

Q9.9. Згідно з інтегральною ознакою для суми збіжного ряду справедлива наступна оцінка. 6

Q9.10. Як формулюється ознака Даламбера збіжності або роз­біжності знакододатного ряду , ? 7

Q9.11. Як формулюється радикальна ознака Коші збіжності або розбіжності ряду з додатними членами ? 7

Q9.12. Який знакозмінний ряд називається абсолютно збіжним, а який умовно збіжним? 8

9. Числові ряди

Q9.1. Що називається числовим рядом?

V1. Числовим рядом називається сума нескінченного числа доданків, якими служать члени довільної числової послідовності .

V2. Числовим рядом називається сума скінченного числа довільнидоданків , де , – деяка числова послідовність.

V3. Числовим рядом називається границя .

V4. Числовим рядом називається сума нескінченного чис­ла доданків, кожний з яких служить елементом деякої скінченної числової множини.

Q9.2. Часткова сума 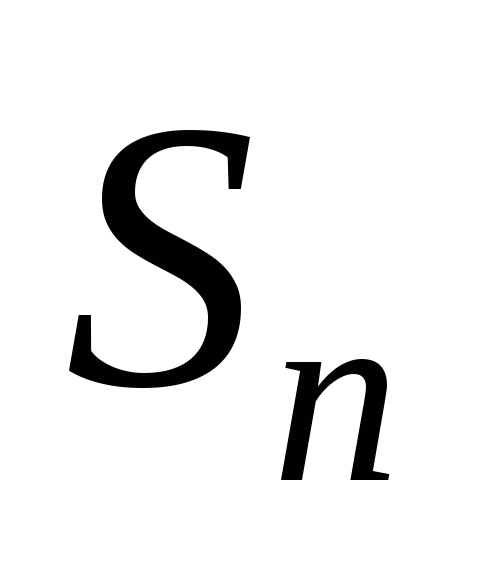ряду визначається рівністю

V1. .

V2. .

V3.

V4. .

Q9.3. Який ряд 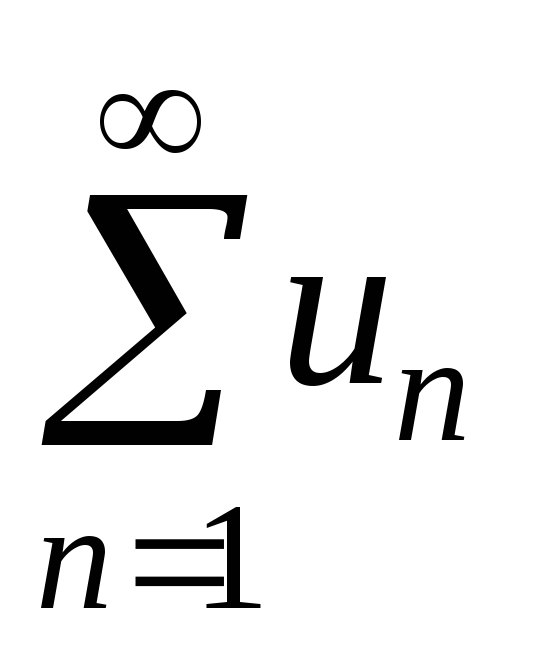називається збіжним? Що називається сумою ряду?

V1. Ряд називається збіжним, якщо , де – часткова сума. Сумою ряду називається число “0”.

V2. Ряд називається збіжним, якщо існує скінченна границя , де – часткова сума. Величина цієї границі називається сумою ряду.

V3. Ряд називається збіжним, якщо не існує границя , де – часткова сума. .

V4. Ряд називається збіжним, якщо , де – часткова сума. .

Q9.4. У чому полягає необхідна умова збіжності ряду?

V1. Якщо ряд збігається, тоді .

V2. Якщо ряд збігається, тоді .

V3. Якщо ряд збігається, тоді .

V4. Якщо ряд збігається, тоді .

Q9.5. У чому полягає основна (перша) ознака порівняння рядів з додатними членами?

V1. Якщо , і , тоді 1) якщо “більший” ряд збігається, то “менший” ряд розбігається; 2) якщо “менший” ряд розбігається, то “більший” ряд збігається.

V2. Якщо , і , тоді обидва ряди збігаються чи розбігаються одночасно.

V3. Якщо , і , тоді 1) якщо “більший” ряд збігається, то “менший” ряд також збігається; 2) якщо “менший” ряд розбігається, то “більший” ряд також розбігається. , тоді обидва ряди збігаються чи розбігаються одночасно.

V4. Якщо , і , тоді 1) якщо “більший” ряд збігається, то “менший” ряд також збігається; 2) якщо “менший” ряд розбігається, то “більший” ряд також розбігається.

Q9.6. У чому полягає гранична (друга) ознака порівняння рядів з додатними членами?

V1. Якщо , і , тоді обидва ряди збігаються чи розбігаються одночасно.

V2. Якщо , і , тоді обидва ряди збігаються чи розбігаються одночасно.

V3. Якщо , і , тоді обидва ряду збігаються чи розбігаються одночасно.

V4. Якщо , і , тоді обидва ряди збігаються і розбігаються одночасно.

Q9.7. У чому полягає інтегральна ознака збіжності або роз­біж­ності ряду 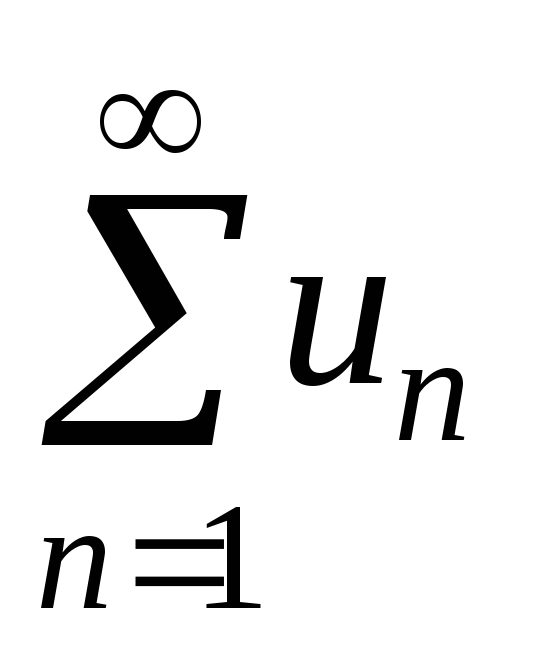з додатними членами 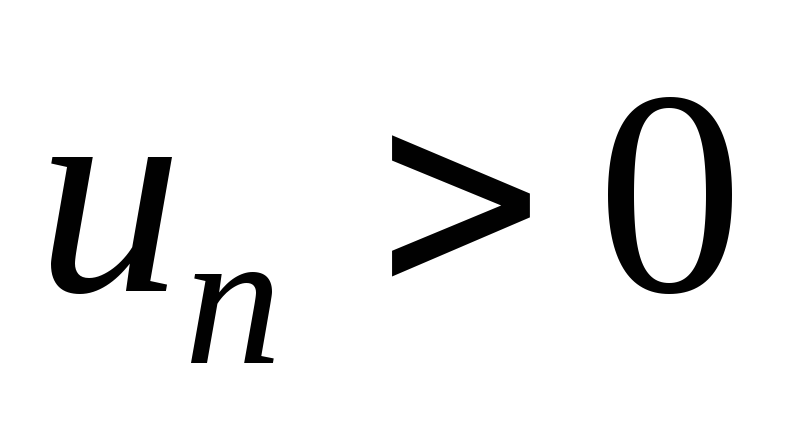? Яка оцінка справедлива для суми цього ряду?

V1. Нехай , , і , , . Тоді ряд і невласний інтеграл збігаються чи розбігаються одночасно. При цьому .

V2. Нехай , , і , , . Тоді ряд і невласний інтеграл збігаються чи розбігаються одночасно. При цьому .

V3. Нехай , , і , , . Тоді 1) якщо невласний інтеграл збігається, то ряд розбігається; 2) якщо невласний інтеграл розбігається, то ряд збі­га­єть­ся. При цьому .

V4. Нехай , , і , , . Тоді ряд і невласний інтеграл збігаються чи розбігаються одночасно. При цьому .

Q9.8. Згідно з інтегральною ознакою для суми збіжного ряду справедлива наступна оцінка.

V1.. V2.. V3.. V4..

Q9.9. Згідно з інтегральною ознакою для суми збіжного ряду справедлива наступна оцінка.

V1.. V2.. V3.. V4..

Q9.10. Як формулюється ознака Даламбера збіжності або роз­біжності знакододатного ряду , ?

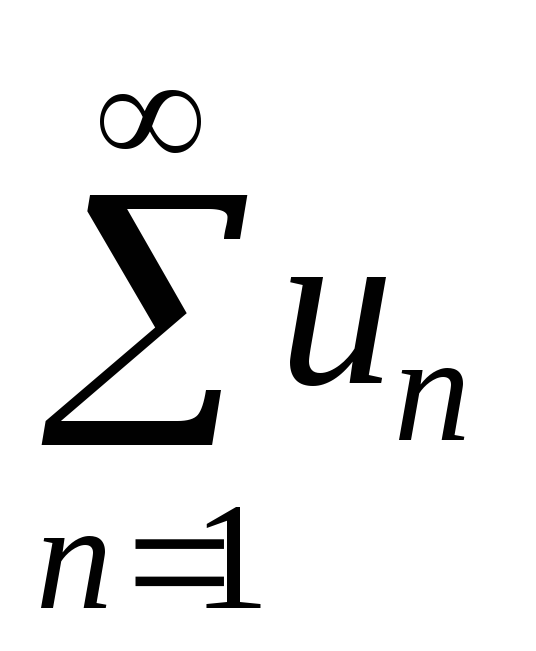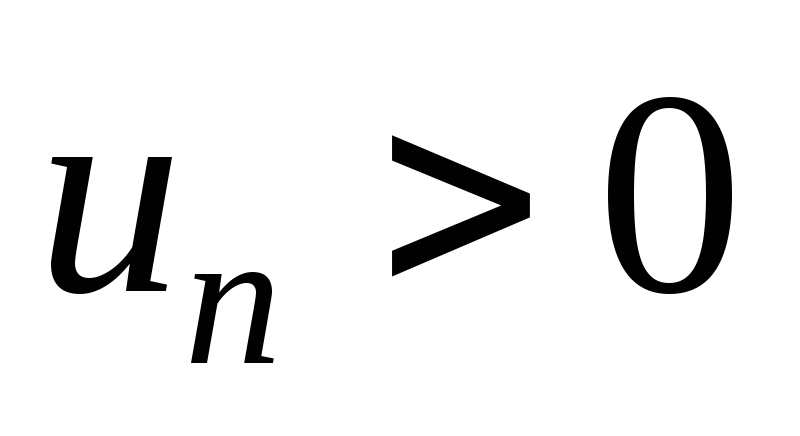V1. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається.

V2. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається.

V3. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається, 3) якщо , то ознака Даламбера на питання про збіжність ряду відповіді не дає.

V4. Якщо для ряду обчислити границю , тоді 1) якщо границя скінченна , то ряд збігається, 2) якщо границя нескінченна , то ряд розбігається, 3) якщо границя взагалі не існує, то ознака Даламбера на питання про збіжність ряду відповіді не дає.

Q9.11. Як формулюється радикальна ознака Коші збіжності або розбіжності ряду 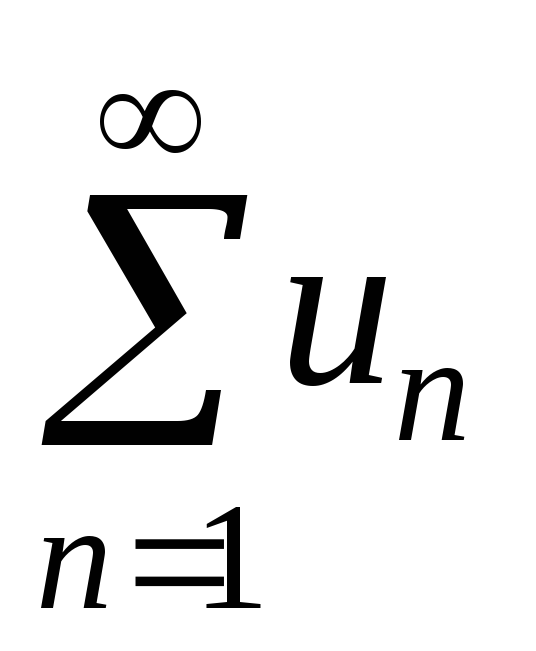з додатними членами ?

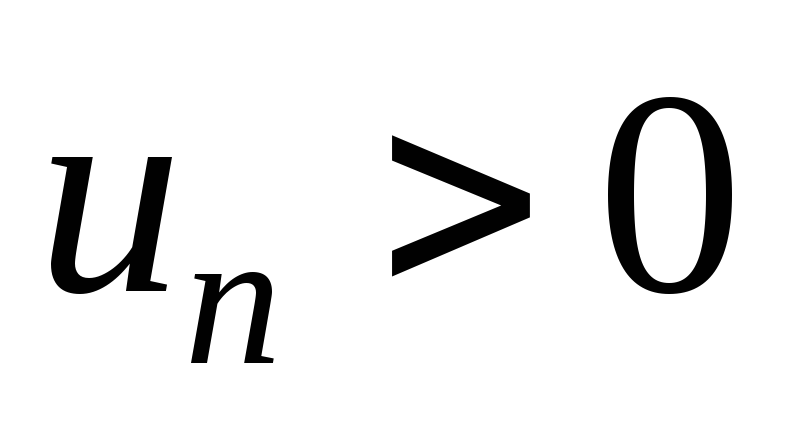V1. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається.

V2. Якщо для ряду обчислити границю , тоді 1) якщо границя скінченна , то ряд збігається, 2) якщо границя нескінченна , то ряд розбігається, 3) якщо границя взагалі не існує, то радикальна ознака на питання про збіжність ряду відповіді не дає.

V3. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається.

V4. Якщо для ряду існує границя , тоді 1) якщо , то ряд збігається, 2) якщо , то ряд розбігається, 3) якщо , то радикальна ознака на питання про збіжність ряду відповіді не дає.

Q9.12. Який знакозмінний ряд 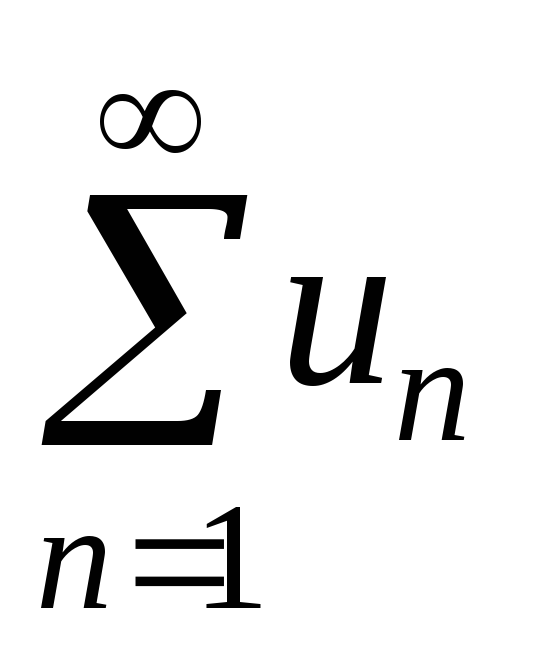називається абсолютно збіжним, а який умовно збіжним?

V1. Знакозмінний ряд називається абсолютно збіжним, якщо збіжним є ряд , складений із модулів його членів. Якщо розбігається, а - збігається, тоді ряд називається умовно збіжним.

V2. Знакозмінний ряд називається абсолютно і умовно збіжним, якщо збіжним є ряд , складений із модулів його членів.

V3. Знакозмінний ряд називається абсолютно і умовно збіжним, якщо розбіжним є ряд , складений із модулів його членів, а сам ряд збігається.

V4. Знакозмінний ряд називається абсолютно і умовно збіжним, якщо збіжним є ряд , складений із модулів його

9