
- •Федеральное агентство по образованию
- •Цель работы: исследование проводимости полупроводников с собственной и примесной проводимостью.
- •1.Краткие теоретические сведения
- •1.1. Зонная теория твердого тела
- •1.1.1. Уравнение шредингера для твердого тела
- •1.1.2. Одноэлектронное приближение
- •1.1.3. Функции блоха
- •1.1.4. Свойства волнового вектора электронов в кристалле. Зоны бриллюэна
- •1.1.5. Энергетический спектр электронов в кристалле. Модель кронига-пенни
- •1.1.6. Заполнение зон электронами. Металлы, диэлектрики, полупроводники
- •1.1.7. Эффективная масса электрона
- •1.2. Электрические свойства полупроводников
- •2.1.1.Энергетические уровни примесных атомов в кристалле
- •2.1.2. Собственная проводимость полупроводников
- •2.1.3.Электропроводность примесных полупроводников
- •2.1.4.Элементарная теория электропроводности полупроводников
- •1.2.5.Статистика электронов и дырок в полупроводниках
- •1.2.5.1.Плотность квантовых состояний
- •1.2.5.2.Функция распределения ферми-дирака
- •1.2.5.3.Степень заполнения примесных уровней
- •1.2.5.4.Концентрация электронов и дырок в зонах
- •1.2.6.Зависимость проводимости полупроводника от температуры
- •2.Методика эксперимента и экспериментальная установка
- •3. Порядок выполнения исследований
- •4. Требования к оформлению отчета
- •5. Контрольные вопросы
- •Примечание
- •Раздел 1 теоретических сведений предназначен только для студентов фрэи, для студентов других специальностей – на усмотрение преподавателя.
- •6.Список литературы
1.2. Электрические свойства полупроводников
2.1.1.Энергетические уровни примесных атомов в кристалле
П рисутствие
в определенном месте кристалла атома
примеси или дефекта структуры приводит
к тому, что на периодический потенциал
решетки
рисутствие
в определенном месте кристалла атома
примеси или дефекта структуры приводит
к тому, что на периодический потенциал
решетки![]() накладывается достаточно сильное
возмущение
накладывается достаточно сильное
возмущение![]() ,
локализованное в некоторой малой области
объемом
,
локализованное в некоторой малой области
объемом![]() с центром в точке
с центром в точке![]() ,
где расположен примесный атом. Наложение
возмущения на потенциал
,
где расположен примесный атом. Наложение
возмущения на потенциал![]() приводит к отщеплению уровней от
разрешенной зоны. (рис.1.2.1). При
приводит к отщеплению уровней от
разрешенной зоны. (рис.1.2.1). При![]()
![]() >0
уровень, соответствующий потолку
разрешенной зоны, поднимается вверх.
Все остальные
>0
уровень, соответствующий потолку
разрешенной зоны, поднимается вверх.
Все остальные![]() уровней остаются без изменения. Если
уровней остаются без изменения. Если![]()
![]() <0,
то уровень минимальной энергии опускается
вниз. Здесь
<0,
то уровень минимальной энергии опускается
вниз. Здесь![]() - среднее значение энергии возмущения
в объеме
- среднее значение энергии возмущения
в объеме![]() .
Таким образом, в запрещенной зоне
появляются разрешенные уровни
.
Таким образом, в запрещенной зоне
появляются разрешенные уровни![]() ,
обусловленные примесями или дефектами.
,
обусловленные примесями или дефектами.
2.1.2. Собственная проводимость полупроводников
Рассмотрим механизм электропроводимости одноатомных полупроводников, например, кремния и германия. Внешняя электронная оболочка атомов таких полупроводников заполнена частично, она содержит четыре электрона: два - в s и два в p – соcтояниях.
При
образовании кристалла четыре валентных
электрона каждого атома из состояния
![]() переходят в гибридное
переходят в гибридное
![]() – состояние с антипараллельными спинами
и образуют четыре ковалентных связи. В
результате каждый атом окружен четырьмя
ближайшими соседями и расположен в
центре тетраэдра. Все электроны находятся
в связанном состоянии. Если такой
полупроводник поместить во внешнее
электрическое поле, то электрический
ток не возникнет, т.к. все ковалентные
связи в решетке завершены, и свободных
носителей заряда нет.
– состояние с антипараллельными спинами
и образуют четыре ковалентных связи. В
результате каждый атом окружен четырьмя
ближайшими соседями и расположен в
центре тетраэдра. Все электроны находятся
в связанном состоянии. Если такой
полупроводник поместить во внешнее
электрическое поле, то электрический
ток не возникнет, т.к. все ковалентные
связи в решетке завершены, и свободных
носителей заряда нет.
Пусть в результате каких-либо воздействий (например, теплоты) в полупроводнике произошел разрыв ковалентной связи, и электрон стал свободным (рис.1.2.2). Процесс превращения связанного электрона в свободный называется генерацией. При уходе электрона ковалентная связь будет незавершенной и иметь избыточный положительный заряд. Вакантное место в ковалентной связи называется дыркой. В целом образец остается электронейтральным, т.к. число электронов равно числу дырок. Свободный электрон может занять место в ковалентной связи и перейти в связанное состояние. Процесс превращения свободного электрона в связанный называется рекомбинацией.
В
отсутствие внешнего электрического
поля свободный электрон, совершая
тепловое движение в кристалле, сталкивается
с дефектами решетки и меняет направление
движения, т.е. движется хаотически. Дырка
может быть заполнена электроном,
перешедшим вследствие теплового
возбуждения из соседней насыщенной
ковалентной связи. При таком переходе
от атома к атому дырка будет совершать
хаотическое движение. Расстояние,
проходимое свободным носителем заряда
между двумя столкновениями, называется
длиной свободного пробега
![]() .
Время между двумя столкновениями – это
время свободного пробега,
.
Время между двумя столкновениями – это
время свободного пробега,
![]() .
Длина свободного пробега равна
.
Длина свободного пробега равна![]() ,
где
,
где![]() –
скорость теплового движения свободного
носителя. Фактическое движение электрона
в кристалле складывается из беспорядочного
теплового и упорядоченного движения,
вызванного действием внешнего
электрического поля. В результате
происходит перемещение всей совокупности
свободных носителей (электронов) с
некоторой средней скоростью. Направленное
движение совокупности свободных
носителей заряда во внешнем электрическом
поле называется дрейфом, а скорость их
направленного движения называется
дрейфовой.
–
скорость теплового движения свободного
носителя. Фактическое движение электрона
в кристалле складывается из беспорядочного
теплового и упорядоченного движения,
вызванного действием внешнего
электрического поля. В результате
происходит перемещение всей совокупности
свободных носителей (электронов) с
некоторой средней скоростью. Направленное
движение совокупности свободных
носителей заряда во внешнем электрическом
поле называется дрейфом, а скорость их
направленного движения называется
дрейфовой.
Электроны насыщенных связей при переходе в вакантное место в связи под действием внешнего электрического поля будут перемещаться против направления поля. Тем самым вакантное место в ковалентной связи – дырка будет перемещаться, но по направлению внешнего электрического поля, что равносильно перемещению по полю положительного заряда. Механизм электропроводности, обусловленный движением электронов по свободным местам в ковалентных связях, называется дырочной электропроводностью.
 Таким образом, в чистом полупроводнике,
не содержащем примесей, осуществляется
электронная и дырочная электропроводность.
Следовательно, электрический ток в
собственном полупроводнике определяется
двумя составляющими – электронным и
дырочным токами, текущими в одном
направлении.
Таким образом, в чистом полупроводнике,
не содержащем примесей, осуществляется
электронная и дырочная электропроводность.
Следовательно, электрический ток в
собственном полупроводнике определяется
двумя составляющими – электронным и
дырочным токами, текущими в одном
направлении.
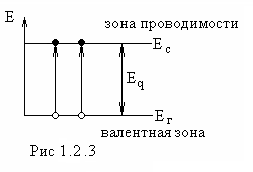
Электропроводность
собственного полупроводника можно
объяснить так. В собственном полупроводнике
при разрыве ковалентной связи появляется
свободный электрон и вакантное место
в ковалентной связи – дырка. Это
равнозначно переходу электрона из
валентной зоны в зону проводимости
(рис.1.2.3). В этом случае все квантовые
состояния
валентной зоны будут заняты электронами,
за исключением одного состояния. Скорость
движения носителя заряда при переходе
в свободное состояние в ковалентной
связи обозначим
![]() .
Тогда суммарная плотность тока всех
электронов валентной зоны:
.
Тогда суммарная плотность тока всех
электронов валентной зоны:
![]()
где
![]() -
объем зоны, т.е. суммарный ток всех
электронов в валентной зоне эквивалентен
току одного электрона, если поместить
его в вакантное место в ковалентной
связи и приписать ему положительный
заряд
-
объем зоны, т.е. суммарный ток всех
электронов в валентной зоне эквивалентен
току одного электрона, если поместить
его в вакантное место в ковалентной
связи и приписать ему положительный
заряд![]() .
.
