1.4.Потенциал. Потенциальная энергия заряда в электростатическом поле

Работа сил электрического поля, созданного зарядом , по перемещению зарядаиз точки 1 в точку 2 равна:

.

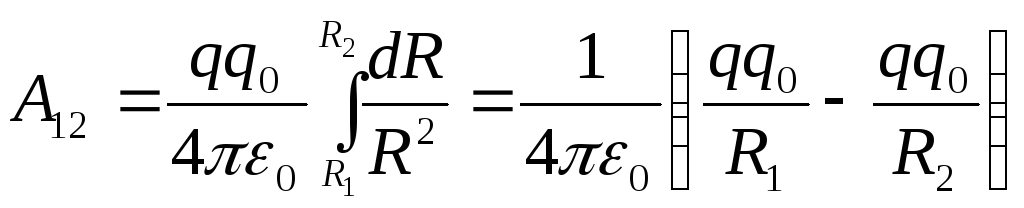Работа сил консервативного поля равна убыли потенциальной энергии:

,

тогда потенциальная энергия заряда в поле зарядаравна:

.

Значение константы выбирается таким, чтобы при удалении заряда на бесконечность (то есть при ) потенциальная энергия обратилась бы в ноль, поэтому

.

Ясно, что разные пробные заряды ив одной и той же точке поля будут обладать разной потенциальной энергиейи. Однако отношениедля всех пробных зарядов будет одинаково. Величина

называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен

.

Если поле создается системой точечных зарядов, то

,

где - расстояние от зарядадо начального положения заряда,- расстояние от зарядадо конечного положения заряда(зарядперемещается силами поля).

Тогда потенциальная энергия зарядав поле системы зарядов:

,

а потенциал

• потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Зная потенциал, можно найти потенциальную энергию заряда в электрическом поле:

.

Работа поля над зарядом:

- работа равна убыли потенциала, умноженной на заряд.

Если заряд удаляется из точки на бесконечность, то работа сил поля равна

следовательно, потенциал численно равен отношению работы, которую совершают силы поля над положительным зарядом при удалении его из данной точки на бесконечность, к величине этого заряда. Потенциал измеряется в вольтах: .

1.5.Связь между напряженностью и потенциалом

Электрическое поле можно описывать либо с помощью векторной величины (силовая характеристика), либо с помощью скаляра(энергетическая характеристика). Сила связана, как известно, с потенциальной энергией:

,

где - оператор Набла,.

Для заряженной частицы в электрическом поле: ,, тогда,, тогда- связь напряженности и потенциала, или, или, или- проекция вектора на произвольное направлениеравна скорости убывания потенциалавдоль направления ,или .

Так как градиент потенциала направлен в сторону его возрастания, а численная величина градиента является мерой быстроты этого возрастания, то можно сказать, что напряженность электрического поля есть мера быстроты спадания потенциала, или, просто, что она равна спаду потенциала.

Вернемся к определению работы поля: ,, отсюда циркуляция вектора на участке 1=2 равна . Интеграл можно брать по любой линии, соединяющей точки 1 и 2, так как работа не зависит от пути.

Для обхода по замкнутому контуру: и- пришли к теореме о циркуляции вектора напряженности электростатического поля.

1.6. Эквипотенциальные поверхности

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:

- уравнение эквипотенциальной поверхности.

При перемещении по эквипотенциальной поверхности на отрезок потенциал не изменяется. Таким образом, касательная к поверхности составляющая вектораравна нулю. Тогда векторнаправлен по нормали к эквипотенциальной поверхности в каждой ее точке, а линии напряженности в каждой точке перпендикулярны к эквипотенциальным поверхностям.

Если эквипотенциальные поверхности построить таким образом, чтобы разность потенциалов для двух соседних поверхностей была одна и та же, то по густоте эквипотенциальных поверхностей можно судить о напряженности поля. Действительно, чем гуще эквипотенциальные поверхности, тем больше, тем больше.

Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.

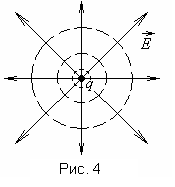
Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.4)

.

Таким образом, эквипотенциальная поверхность этого заряда будет сферой радиуса с центром в точке заряда. Силовые же линии, как мы установилиранее, расходятся радиально от заряда если он , или сходятся к заряду, если он “-”. То есть векторперпендикулярен эквипотенциальным поверхностям.