Министерство образования и науки рф

ФГБОУ ВПО РЫБИНСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П.А. СОЛОВЬЕВА

КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ

	УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ « » 2013 г. Зав.каф. Пиралишвили Ш.А.

Лаборатория «Физические основы механики»

ЛАБОРАТОРНАЯ РАБОТА№ ФМ-2

Изучение прецессии лабораторного гироскопа

	Переработано: к.т.н. доцент
	Каляева Н.А. _________
	Рецензент: к.п.н., доцент  Попкова Е.А. ­ _________

Рыбинск 2013

ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ: При включении прибора в сеть тумблеры прибора должны находиться в положении «выключено». При работе нужно следить за состоянием прово­дов, идущих от датчика, укреплённого на рамке гироскопа, не допускать их перекручивания. Без необходимости раскручивать гироскоп запрещается.

ЦЕЛЬ РАБОТЫ: Изучение гироскопического эффекта, определение частоты прецессии лабораторного гироскопа.

ПРИБОРЫ И ОБОРУДОВАНИЕ: Лабораторный гироскоп, линейка, счётчик числа импульсов (оборотов) и времени (СИВ-1)

1. Краткие теоретические сведения

Абсолютно твёрдым телом называется тело, которое ни при каких условиях не может деформироваться, то есть расстояние между двумя точками (или точнее между двумя частицами) этого тела остаётся постоянным.

При вращении твёрдого тела все его точки движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.

1.1 Кинематика вращательного движения

Рис. 1.1.1

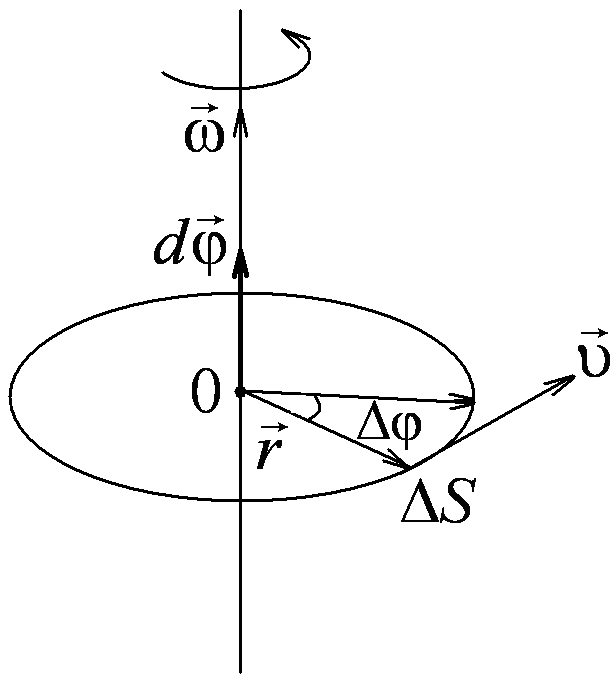
Пусть некоторая точка движется по окружности радиуса r (рис. 1.1.1). Её положение через промежуток времени зададим углом. Элементарные (бесконечно малые) углы поворота рассматриваются как векторы. Модуль вектораравен углу поворота, а его направление определяется поправилу правого винта (рис.1.1.1).

Векторы, направления которых связываются с направлением вращения твёрдого тела, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определённых точек приложения: они могут откладываться из любой точки оси вращения.

Быстроту вращения характеризует угловая скорость. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

.

Вектор направлен вдоль оси вращения в соответствии с правилом правого винта, т.е. так же, как и вектор(рис. 1.1.1). Единицей угловой скорости служит радиан в секунду (рад/с).

Величина линейная скорости точки (рис. 1.1.1):

.

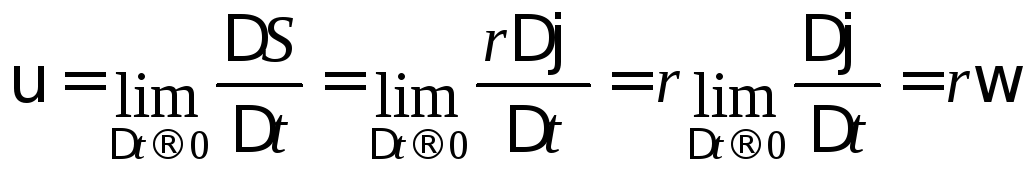Направлена линейная скорость по касательной к траектории.

В векторном виде формулу для линейной скорости можно написать как векторное произведение угловой скорости и радиус-вектора, проведённого из центра окружности в рассматриваемую точку (рис.1.1.1):

Если , то вращение называется равномерным и его можно характеризоватьпериодом вращения – временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол. Так как промежутку временисоответствует угол, то

, откуда .

Число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени, называется частотой вращения:

, откуда .

Быстроту изменения угловой скорости характеризует угловое ускорение – векторная величина, равная первой производной угловой скорости по времени или второй производной от угла поворота по времени:

Рис. 1.1.2

Модуль углового ускорения равен: .

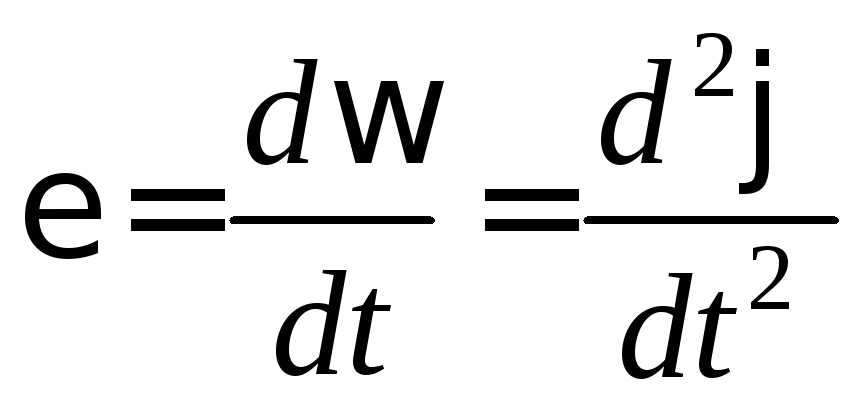При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору, при замедленном – противонаправлен ему (рис. 1.1.2).

Ускорение производной точки твердого тела, вращающегося вокруг неподвижной точки О или неподвижной оси, проходящей через эту точку, называютлинейным ускорением. Оно равно:

где 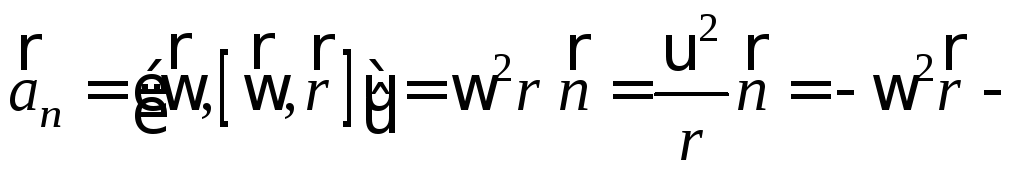нормальное или центростремительное ускорение;- касательное или тангенциальное ускорение. Здесь- единичный вектор, направленный по нормали в данной точке траектории;- единичный вектор, направленный по касательной к траектории в направлении скороститочки (рис.1.1.3).

Рис. 1.1.3

Нормальное ускорение характеризует быстроту изменения направления вектора скорости точки, оно направленно по нормали к траектории к центру кривизны. Величина нормального ускорения , где - радиус кривизны траектории в данной точке.

Касательное ускорение характеризует быстроту изменения модуля скорости, оно направленно по касательной к траектории. Векторы исовпадают по направлению, т.е>0, при ускоренном движении точки; векторыивзаимно противоположны по направлению, т.е<0 при замедленном движении точки, ипри ее равномерном движении. Величина касательного ускорения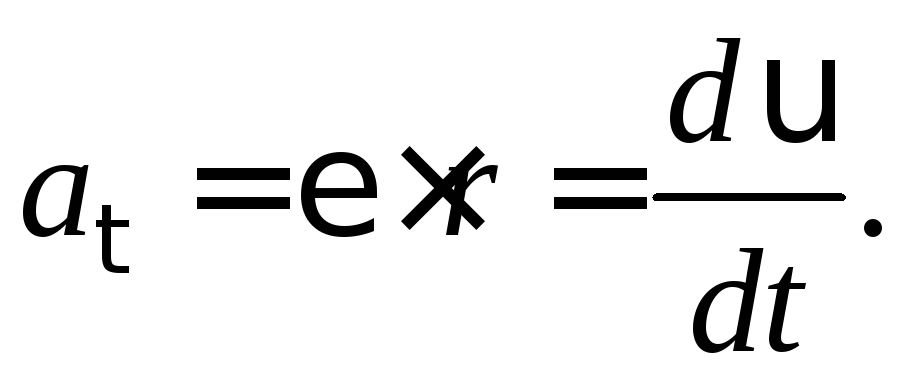

Учитывая, что векторы ивзаимно перпендикулярны, величина полного линейного ускорениябудет определяться по теореме Пифагора:

.

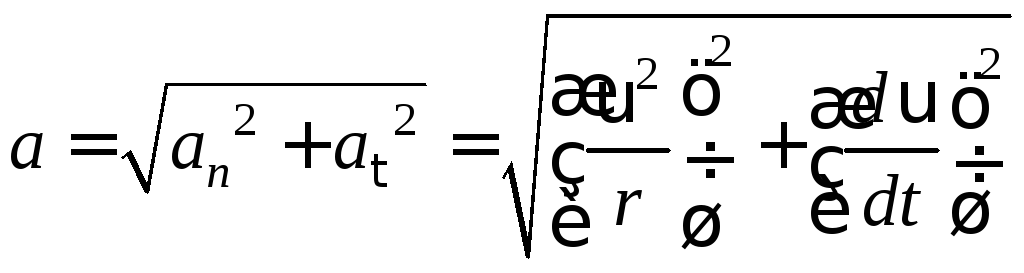Таким образом, связь между линейными (длина пути S, пройденного точкой по дуге окружности радиуса ; линейная скорость ; тангенциальное ускорение ; нормальное ускорение) и угловыми величинами (угол поворота, угловая скорость, угловое ускорение) выражается следующими формулами:

, ,,.

В случае равнопеременного движения точки по окружности ():

; ,

где – начальная угловая скорость; знак «+» соответствует равноускоренному вращательному движению, знак «–» – равнозамедленному вращательному движению.