Перевод дробных чисел из одной позиционной системы в другую
Предположим, что правильное дробное число Хуже переведено в новую позиционную систему счисления с основаниемb. Тогда числоХможет быть записано в виде
X=a–1b–1 + a–2b–2 +…+ a–mb–m.
Умножим левую и правую части этого выражения на основание системы счисления b:
X·b=a–1+(a–2b–1 +a–3b–2+…+ a–mb–m+1).
В правой части этого выражения есть целая часть a–1и дробная часть, заключенная в скобки. Таким образом, после первого умножения дробного числаХна основание системы счисления получили первую цифру числаХв новой системе счисления.
Умножим теперь часть последнего выражения, стоящую в скобках, на основание bновой системы счисления. Получим:
(a–2b–1 +a–3b–2+…+ a–mb–m+1)·b= a–2+(a–3b–1 +a–4b–2+…+ a–mb–m+2).
В правой части выражения снова имеем целую и дробную части. Получили вторую цифру a–2числаХв новой системе счисления.
Продолжая процесс умножения на основание системы счисления, получим все цифры переведенного числа с требуемой степенью точности. Все умножения выполняются в исходной системе счисления.
Пример 6. Перевести из десятичной системы счисления в двоичную дробное число 0,34375, ограничиваясь шестью знаками.
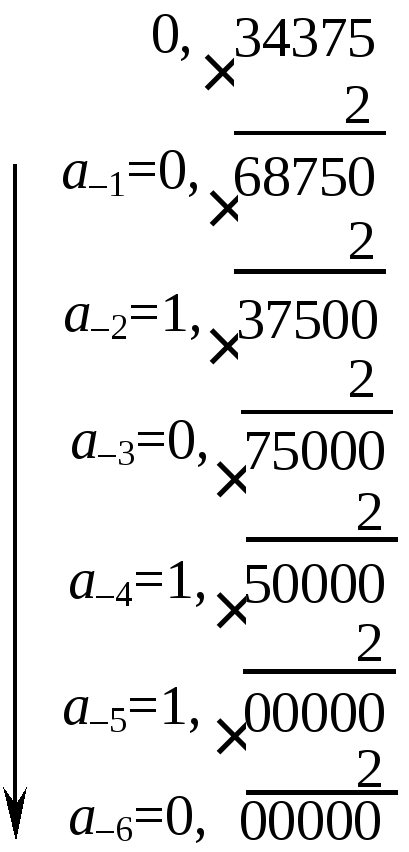
Ответ: Х=0,34375(10)=0,010110(2). Проверка: 010110(2)=02–1 + 12–2 + 02–3 +
+ 12–4 + 12–5 + 02–6=1/4 + 1/16 + 1/32 = 0,25 + 0,0625 +0,03125 = 0,34375(10). Получился точный ответ.
П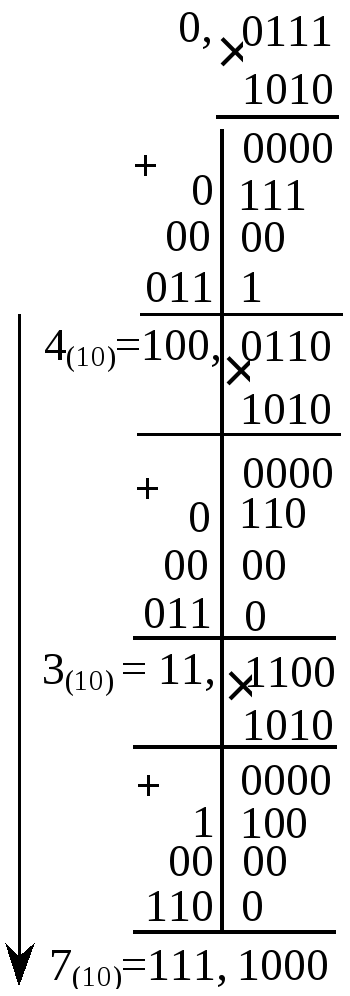
ример
7. Перевести числоХ=0,0111 из двоичной
системы в десятичную с тремя знаками
после десятичной запятой.
Ответ: 0,0111(2)=0,437(10). Получился неточный ответ, т. к. в дробной части последней строки не все цифры нулевые. Точный ответ: 0,0111(2)=0,4375(10).
В этом примере перевод двоичного числа в десятичную систему счисления сводится к умножению дробной части на основание системы счисления 1010(2)=10(10). Нам неудобно делать вычисления в недесятичной системе. Поэтому на практике перевод чисел из недесятичной системы счисления в десятичную сводится к подсчету суммы произведений степеней основания на соответствующую цифру, как это сделано в примере 5. При этом расчеты ведутся в десятичной системе счисления.
Перевод числа в данном примере: 0,0111(2)= 02–1+12–2+12–3+12–4= =0,25+0,125+0,0625=0,4375(10).
Перевод неправильных дробей из одной позиционной системы счисления в другую
Неправильные дроби из одной позиционной системы счисления в другую переводят в два этапа: отдельно переводят целую и дробную части по соответствующим правилам, приведенным ранее, после чего записывают число в новой системе счисления.
Пример 8. Перевести из десятичной системы в двоичную неправильную десятичную дробь Х=92,3475.
Решение. Сначала переводим последовательным делением целую часть и получаем (см. пример 1) 92(10)=1011100(2). Далее переводим методом последовательных умножений дробную часть и получаем (пример 5) 0,34375(10)=0,010110(2). После этого записываем окончательный результат:
92,3475(10)= 1011100,010110(2).
Прямой и обратный перевод из двоичной в восьмеричную и шестнадцатеричную системы счисления
ЭВМ производит арифметические и логические операции над исходными числами (операндами) в двоичной системе счисления, которая называется основной. Запись чисел в двоичной системе громоздка и неудобна для человека, поэтому при записи программ широко применяются вспомогательные восьмеричная и шестнадцатеричная системы счисления. Основаниями этих систем счисления являются целые степени числа 2. Это значительно облегчает перевод их в двоичный код.
Для перевода чисел из двоичной системы счисления в систему счисления с основанием 2kнеобходимо разбить исходное двоичное число на группы поkразрядов, начиная от запятой (вправо и влево). Каждая из этих групп рассматривается как целое число и заменяется одной цифрой в соответствии с таблицей 2. При переводе из двоичной системы счисления в восьмеричную число разбивается на триады, а при переводе в шестнадцатеричную – на тетрады.
Пример 9. Перевести число Хиз двоичной системы в восьмеричную.
X=10010101010100,01101001.
Разбиваем разряды исходного числа на триады. При разбиении в неполные группы справа и слева дописываются нули:
X=010 010 101 010 100, 011 010 010.
Теперь заменяем каждую группу восьмеричной цифрой в соответствии с таблицей 2. Получаем
X=22524,322(8).
Пример 10. Перевести число Хиз двоичной системы в шестнадцатеричную.
X=10010101010100,01101001.
X=0010 0101 0101 0100, 0110 1001=2554,69(16).
Пример 11. Перевести число Хиз двоичной системы в шестнадцатеричную.
X=1100111011010,1011111010.
Разбиваем число на тетрады:
X=0001 1001 1101 1010, 1011 1110 1000=19DA,BE8(16).
Двоичная система счисления может использоваться как промежуточная при переводе чисел из восьмеричной в шестнадцатеричную систему и обратно.
Пример 12. Перевести число X=37520,610342 из восьмеричной системы в шестнадцатеричную, используя двоичную систему в качестве промежуточной.
Переводим исходное число в двоичную систему счисления путем замены каждой восьмеричной цифры в группу из трех двоичных разрядов (триаду):
X=37520,610342(8)=011 111 101 010 000, 110 001 000 011 100 010(2).
Разбиваем полученное двоичное число на тетрады:
X=011111101010000,110001000011100010=0011 1111 0101 0000,1100 0100 0011 1000 1000.
Заменяем каждую тетраду одной шестнадцатеричной цифрой. Получим
X=3F50,C4388(16).
При ручном переводе чисел из десятичной системы счисления в двоичную часто удобнее сначала перевести число в восьмеричную систему счисления, а затем из восьмеричной – в двоичную, чем выполнять перевод десятичного числа сразу в двоичную систему.
Пример 13. Перевести десятичное число 92 в двоичную систему счисления.
Переводим число в восьмеричную систему.
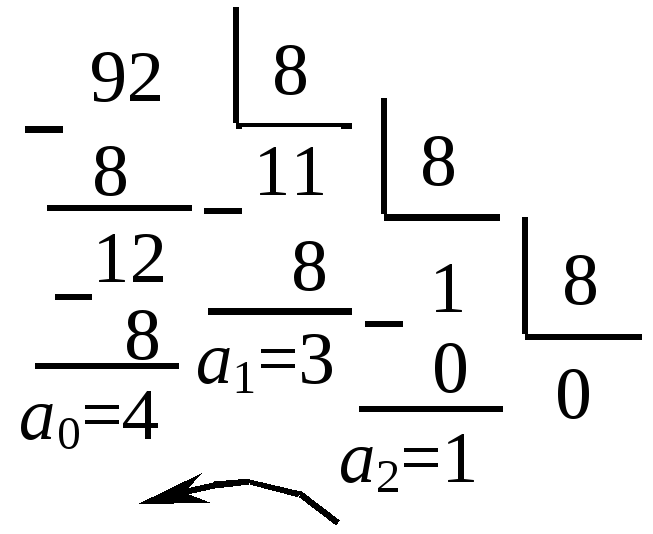
92(10)=134(8)
Переводим восьмеричное число в двоичное заменой каждой восьмеричной цифры двоичной триадой.
134(8)=001 011 100=1011100.
Существуют и другие способы перевода чисел из одной позиционной системы счисления в другую.