Федеральное агентство по образованию

РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ МИФИ

Дифференциальные уравнения и ряды

Методическое пособие

по курсу высшей математики

для 4-го семестра вечернего факультета

Москва 2010

УДК 517.918(07)

ББК 22.161/6я7

К 72

Дифференциальные уравнения и ряды: Методическое пособие по курсу высшей математики для 4-го семестра вечернегофакультета.М.: НИЯУ МИФИ, 2010. 82 c.

Пособие написано на основе опыта чтения лекций и проведения семинаров в группах вечернего факультета НИЯУ МИФИ. Сформулированы основные определения и теоремы, разобрано большое количество примеров (указаны номера по задачнику Г.Н.Бермана). Приведены списки контрольных вопросов по теме каждого занятия. Подобраны задачи в количестве, достаточном для проведения семинаров.

Пособие предназначено преподавателям, проводящим семинарские занятия по высшей математике на 4-ом семестре вечернего факультета, а также студентам всех специальностей вечернего факультета НИЯУ МИФИ.

Рекомендовано к изданию редсоветом МИФИ

 Национальный исследовательский ядерный университет

МИФИ 2010

Редактор

Верстка книги полностью соответствует представленному

авторами оригиналу-макету.

ЛР №020676 от_____.10.

Подписано в печать______ 2010. Формат 60х84 1/16.

Печ. л. 5,15. Уч.-изд. л. ,15. Тираж 200 экз.

Изд. № _____. Заказ №

Национальный исследовательский ядерный

университет МИФИ .

Типография МИФИ.

115409, Москва, Каширское ш., 31

Часть 1. Обыкновенные дифференциальные уравнения

Занятие 1. Уравнения с разделяющимися переменными. Однородные уравнения.

Упражнения на занятии: 3901, 3903, 3905, 3907, 3909, 3913, 3915, 3935, 3937, 3939, 3941, 3945.

На дом № 3902, 3904, 3906, 3914, 3916, 3936, 3938, 3946.

Дифференциальным уравнением(ДУ) называется уравнение, которое помимо неизвестных функций содержит их производные (или дифференциалы).

Если неизвестные функции, входящие в ДУ, зависят только от одной независимой переменной, то ДУ называется обыкновенным ДУ (ОДУ).

Уравнение

, (1.1)

где называется обыкновенным дифференциальным уравнением относительно функциина промежутке.

Число nназывается порядком уравнения (1.1). Функцияназывается частным решением ОДУ (1.1), если после заменына,на, ...,науравнение обращается в тождество на промежутке. (Предполагается, что- достаточно гладкая функция.)

График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Дифференциальное уравнение вида

, (1.2)

где определена в областиDна плоскостиXOY, называется ОДУ первого порядка, разрешенным относительно производной.

Задачей Кошиназывают задачу нахождения решенияуравнения (1.2), удовлетворяющего начальному условию

, где.

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку .

Общим решениемдифференциального уравнения (1.2) называется функция, зависящая от одной произвольной постояннойС, если

1) функция удовлетворяет дифференциальному уравнению при любых допустимых значенияхС;

2) для любого частного решения уравнения (1.2) можно подобрать постояннуюC, такую, чтона.

Общее решение дифференциального уравнения определяет в некоторой области плоскости XOYсемейство интегральных кривых, зависящих от произвольной постояннойС. Частному решению соответствует фиксированная интегральная кривая из этого семейства.

Пример 1.1.Проверить, что функцияесть общее решение дифференциального уравненияи найти частное решение, удовлетворяющее начальному условию. Дать геометрическое истолкование результата.

Решение.Функцияудовлетворяет данному дифференциальному уравнению при любых значениях постояннойС, так как.

Полагая и, получим частное решениепри. Общее решениеопределяет в плоскостиXOYсемейство параллельных наклонных прямых с угловым коэффициентом, частное решениеопределяет наклонную прямую, проходящую через начало координат.

Дифференциальное уравнение вида

называется уравнением с разделенными переменными.

Уравнение вида:

называется уравнением с разделяющимися переменными.

Делением на произведение оно приводится к уравнению с разделенными переменными

.

Замечание. Деление на произведениеможет привести к потере частных решений, обращающих в нуль произведение.

Рассмотрим примеры.

3901.Найти общее решение уравнения:

.

Решение. Преобразуем уравнение:

.

Чтобы разделить переменные в уравнении, умножим его на выражение .

После алгебраических преобразований получим:

или.

Проинтегрировав, получим:

.

После потенцирования: ,.

Далее, при делении на скобку могли быть потеряны решенияи. Подстановка их в дифференциальное уравнение обращает его в тождество. Следовательно, это тоже решения.

3903.Найти общее решение уравнения:

Решение. Запишем уравнение в таком виде:

.

Интегрируя, получим общее решение уравнения:

,,

3913. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

; .

Решение. Проведем разделение переменных и несложные тригонометрические преобразования:

.

После интегрирования получим:

.

Далее, потенцируем

и подставляем начальные условия:

.

Ответ:.

Дифференциальное уравнение называетсяоднородным,если его можно представить в виде

.

Вводя новую неизвестную функцию имеем,После подстановки получаем уравнение с разделяющимися переменными:

.

Пример 1.2..

Решение.Пусть, или, ТогдаПодставляя в уравнениеи, получим

.

Разделим переменные и проинтегрируем:

или,

а так как , то, обозначая, получаем

, где.

После обратной замены переменных имеем

или

При разделении переменных имело место деление на выражение , что могло привести к потере решений, обращающих в нуль это выражение. Здесь- независимая переменная, а изследует, откуда. Проверкой убеждаемся, что функцииитакже являются решениями дифференциального уравнения, поэтому общее решение:

,,.

3937.Решить уравнение

Это – однородное уравнение. Замена переменных ,позволит разделить переменные:

(В числителе первого интеграла прибавили и вычли и разделили почленно.) После интегрирования имеем:

Возвращаясь к старым переменным, получим ответ:

,.

Контрольные вопросы.

1. Что называется дифференциальным уравнением?

2. Что такое порядок дифференциального уравнения?

3. Что называется интегральной кривой дифференциального уравнения?

4. Что называется задачей Коши для дифференциального уравнения?

5. Что называется общим решением дифференциального уравнения?

6. Запишите общий вид уравнения с разделенными переменными.

7. Запишите общий вид уравнения с разделяющимися переменными. Опишите метод решения.

8. Запишите общий вид однородного уравнения. Опишите метод решения.

Занятие 2. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли.

Упражнения на занятии: 3955, 3957, 3959, 3961, 3962, 3965, 3967, 4043.

На дом. № 3956, 3958, 3960, 3966, 3988, 3990, 4000.

Линейным дифференциальным уравнением первого порядканазывается уравнение, линейное относительно неизвестной функциии её производной первого порядка. Оно имеет вид:

,, (2.1)

где и-- известные функции независимой переменной, непрерывные на промежутке.

Если , то уравнение (2.1) называетсялинейным однородным, исходное же уравнение (2.1) с правой частьюназываетсялинейным неоднороднымдифференциальным уравнением. Однородное уравнение является уравнением с разделяющимися переменными и имеет общее решение такого вида:

.

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение ищется в виде

, (2.2)

где -- неизвестная функция от. В результате подстановки (2.2) в уравнение (2.1) получаем дифференциальное уравнение, интегрируя которое, удаётся найти функцию.

Пример 2.1.Решить уравнение

. (2.3)

Решение.Однородное уравнение, соответствующее данному неоднородному, имеет вид:, его общее решение,. Общее решение уравнения (2.3) ищем в виде

, (2.4)

где - неизвестная функция. Подставляя (2.4) в (2.3), получаем уравнение , откуда.

В итоге, общее решение уравнения (2.3):

,.

Может оказаться, что дифференциальное уравнение линейно относительно как функции независимой переменной, т.е. имеет такой вид:

.

Пример 2.2..

Решение.Данное уравнение является линейным относительно функциии её первой производной:

. (2.5)

Сначала решаем соответствующее однородное уравнение

.

Его общее решение имеет вид ,. Решение уравнения (2.5) ищем в виде

, (2.6)

где - неизвестная функция. Подставляя (2.6) в (2.5), имеем:

откуда

.

Интегрируя по частям, получим:

В итоге:

. (2.7)

Подставляя (2.7) в (2.6), получаем общее решение исходного дифференциального уравнения:

.

3957.Решить уравнение

Решение.Разделим налевую и правую части уравнения. Посколькуне обращается в нуль нигде на осиОX, никакие решения уравнения потеряны не будут. Получим:

. (2.8)

Однородное уравнение, соответствующее данному неоднородному:

.

Проинтегрируем, предварительно разделив переменные:

.

Общее решение уравнения (2.8) ищем методом вариации постоянной, подставив в (2.8)

, (2.9)

где C(x)- неизвестная функция, получим:

,

откуда

;.

Подставив в (2.9), получим общее решение исходного дифференциального уравнения:

,

3961.Решить уравнение.

Решение.Это уравнение становится линейным, еслисчитать функцией независимой переменной. Тогда уравнение примет вид:

(2.10)

Интегрируя соответствующее однородное уравнение, получаем:

.

Решение уравнения (2.10) ищем в виде

. (2.11)

Подставив (2.11) в (2.10), получим:

;

Интегрируя по частям дважды, имеем:

Зная , находим общее решение исходного дифференциального уравнения:

.

Уравнение Бернуллиимеет вид. Приионо является линейным, при других значенияхприводится к линейному виду с помощью перехода к новой неизвестной функции.

Пример 2.3.Решить уравнение

. (2.12)

Решение.Разделив обе части уравнения на, получим

.

При этом следует учесть, что является частным решением исходного уравнения. Сделав замену переменных, заметим, что. В результате уравнение (2.12) будет преобразовано к виду

. (2.13)

Решая однородное уравнение находим

,

Подставив в (2.13), получим,

откуда:

и

Общее решение исходного уравнения:

.

4043. Решить уравнение Бернулли

Разделив все на получим:

.

Переходим к новой неизвестной функции , тогдаи уравнение принимает вид

(2.14)

Соответствующее однородное уравнение решаем методом разделения переменных:

.

Решение неоднородного уравнения ищем в виде

.

После подстановки в (2.14) получаем уравнение

,

из которого после сокращений получаем:

.

Решение уравнения:

Контрольные вопросы.

1. Дайте определение линейного дифференциального уравнения первого порядка.

2. В каком случае линейное дифференциальное уравнение называется однородным, а в каком – неоднородным?

3. В чем состоит метод вариации произвольной постоянной?

4. Какой вид имеет уравнение Бернулли? Опишите метод решения уравнения Бернулли.

Занятие 3. Уравнения в полных дифференциалах.

Упражнения на занятии: 4050, 4051, 4052, 4053, 4058, 4061.

На дом. № 4054, 4073, 4059, 4062, 4074.

Дифференциальное уравнение

(3.1)

называется уравнением в полныx дифференциалаx, если его левая часть представляет собой полный дифференциал некоторой функции, т.е.

Теорема.Пусть функции

,

непрерывны в односвязной области D плоскостиXOY. Выражение есть полный дифференциал только тогда, когда выполнено условие

вD.(3.2)

Пример 3.1.Решить уравнение

. (3.3)

Решение.Проверим, является ли (3.3) уравнением в полных дифференциалах:

=

=

следовательно, , т.е. (3.3) – уравнение в полных дифференциалах и, поэтому

=.

Частную производную найденной функцииприравняемQ(x,y)=cosxy, что даёт

cosxy+f'=cosxy,

откуда следует:

, и .

Общий интеграл уравнения:

,.

При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получатся легко интегрируемые комбинации. В частности, можно выделять полные дифференциалы, используя известные формулы:

,,и т.п.

Пример 3.2.Решить уравнение

. (3.4)

Решение.Здесь,, следовательно, (3.4) – уравнение в полных дифференциалах. Сгруппируем его члены так:

Тогда

, ,

и уравнение (3.4) можно записать в виде:

или

Следовательно,

есть общий интеграл дифференциального уравнения (3.4).

Контрольные вопросы.

1. Сформулируйте определение уравнения в полных дифференциалах.

2. Опишите метод решения уравнений в полных дифференциалах.

3. Опишите метод выделения интегрируемых комбинаций.

Занятие 4. Особые решения дифференциальных уравнений. Огибающая семейства интегральных кривых. Уравнение Клеро.

Упражнения на занятии: 4117, 4119, 4120, 4123.

На дом.№ 4118, 4122, 4125.

Решение дифференциального уравнения

(4.1)

называется особым, если в каждой его точке нарушается свойство единственности, т.е. если через каждую его точку , кроме этого решения, проходит и другое решение, имеющее в точкету же касательную, но не совпадающее с решениемв сколь угодно малой окрестности точки . График особого решения будем называтьособой интегральной кривой.

Если две кривые иимеют общую точку и в этой точке общую касательную, то говорят, что кривые касаются в этой точке.

Условия касания кривыx в т. :

.

Кривая, которая касается каждой кривой семейства

в одной или нескольких точках и притом вся состоит из точек касания, называется огибающейданного семейства.

Теорема. Пусть– семейство кривых, причем

в точке.

Тогда в некоторой окрестности точки точки, лежащие на огибающейэтого семейства кривых, удовлетворяют системе:

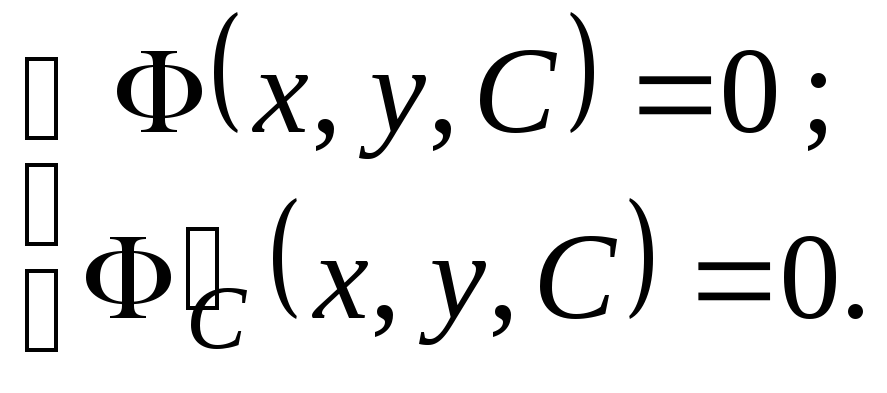(4.2)

Замечание.Теорема утверждает, что если– огибающая, то всякая её точка удовлетворяет (4.2). Обратное неверно, т.е. определяемая (4.2) кривая может и не быть огибающей. (Теорема даёт лишь необходимое условие огибающей.) Из решений системы (4.2) огибающие отбираются непосредственной проверкой условий касания.

Если из уравнений системы (4.2) удается исключить параметр C, то уравнение огибающей получается в явном виде, как.

Пример 4.1.. Это уравнение описывает семейство окружностей радиуса, центры которых лежат на осиOX, а параметресть смещение центров относительно начала координат.

Продифференцировав уравнение по параметру , получим. Подставив в уравнениеи исключив тем самым параметр, получим, или иначеи- уравнения двух огибающих семейства кривых.

Красивый наглядный пример особого решения дает уравнение Клеро, имеющее вид

. (4.3)

При интегрировании его применим метод введения параметра. Приняв y'=p и подставив в (4.3), получим

. (4.4)

Далее, продифференцировав уравнение (4.4) по переменной , получим

,

откуда

.

Здесь либо 1) , либо 2).

Из 1) следует . Подставив это в уравнение (4.4), получим- уравнение семейства прямых с угловым коэффициентом, пересекающих осьOYв точках. Используя 2), решение можно представить в параметрическом виде:

(4.5)

где . Нетрудно увидеть, что интегральная кривая, определяемая (4.5), является огибающей семейства прямых . Действительно, в этом случаеи огибающая определяется уравнениямии, или

(4.5')

где , что отличается от (4.5) лишь обозначениями. Если удается исключитьСиз (4.5'), то особое решение можно получить в явном виде.

4119. Решить уравнение

. (4.6)

Решение. Подставим, получим

. (4.6')

Продифференцировав по, имеем

,

откуда

;;;.

Подставив в выражения для и, получим систему уравнений:

(4.7)

Подставив в первое уравнение, найдем

(4.8)

Это уравнение параболы, симметричной относительно оси OX. Семейство прямых, описываемых первым уравнением системы (4.7), есть семейство касательных к этой параболе. Таким образом, парабола (4.8) может рассматриваться как огибающая семейства собственных касательных. Такое геометрическое истолкование характерно для уравнения Клеро.

Другие виды уравнений, решаемых методом введения параметра.

А.Уравнение видаразрешимо относительноy:

.

Полагаем , тогда. Дифференцируем последнее уравнение и, заменивdyнаpdx, получаем, откуда

и,.

Это общее решение дифференциального уравнения в параметрической форме.

Пример 4.2.Решить уравнение

(a иb– постоянные).

Решение.Положим, тогда,

или,

откуда

и.

Общее решение будет иметь вид:

.

В. Уравнение видаразрешимо относительно , т.е.. Полагая, получим. Кроме того,т.е.и. Проинтегрировав, найдем общее решение дифференциального уравнения в параметрической форме:

,.

Пример 4.3.Решить уравнение

Решение.Положим, тогда,

В итоге

,.

4117. Решить уравнение .

Решение.Это уравнение Клеро. После введения параметрауравнение имеет вид:

. (4.9)

Взяв полный дифференциал и заменив на, получим:

, откуда.

Если , то. Подставив в (4.9), получаем

. (4.10)

Далее, подставив в уравнение, имеем

.(4.11)

Очевидно, что (4.11) может быть получено из (4.10) дифференцированием по параметру C, следовательно, в соответствии с изложенным ранее, система уравнений (4.10), (4.11) в параметрической форме описывает особое решение уравнения, графиком которого является огибающая семейства прямых, заданных общим решением (4.10). Исключив параметрCиз системы уравнений (4.10), (4.11), найдем уравнение огибающей в явном виде:

.

Контрольные вопросы.

1. Какое решение дифференциального уравнения называется особым?

2. Что такое особая интегральная кривая?

3. Какая кривая называется огибающей семейства кривых?

4. Запишите общий вид уравнения Клеро, опишите метод решения.

5. Перечислите некоторые типы уравнений, решаемых методом введения параметра.

Занятие 5. Дифференциальные уравнения старших порядков.

Упражнения на занятии: 4157, 4163, 4166, 4171, 4177, 4183, 4190, 4209, 4213, 4214.

На дом. № 4155, 4156, 4159, 4160, 4163, 4169, 4189, 4208.

Дифференциальное уравнение -го порядка имеет вид

, ,

или, если оно разрешено относительно ,

. (5.1)

Здесь функция переменнойопределена в некоторой области,

а D– область в

Всякая функция , определенная ираз дифференцируемая на промежутке, называется решением этого уравнения, если она обращает его в тождество при подстановке.

Задача нахождения решения уравнения (5.1), соответствующего начальным условиям

(5.2)

называется задачей Кошидля уравнения (5.1) (Здесь). Условия (5.2) называютсяусловиями Коши или начальными условиями.

Общим решениемдифференциального уравнения-го порядка (5.1) называется множество всех его решений. Оно обычно представляется формулой , содержащейnпроизвольных независимых между собой постоянных,, таких, что, если заданы начальные условия (5.2), то могут быть найдены все значения, при которых

будет частным решением уравнения (5.1), удовлетворяющим условиям (5.2).

В процессе интегрирования уравнения -го порядка иногда удается получить уравнение более низкого порядка, эквивалентное исходному. Такое уравнение называетсяпромежуточным интегралом.

Рассмотрим три вида дифференциальных уравнений, допускающих понижение порядка.

1.Уравнение вида. После-кратного интегрирования получается общее решение

Пример 5.1.Решить уравнение.

Решение.Интегрируя последовательно данное уравнение, имеем:

.

2.Уравнение, не содержащее искомой функции и её производных до порядкавключительно:

.

Порядок уравнения можно понизить на kединиц заменой

.

Уравнение примет вид:

.

Из этого уравнения определяем

,,

а затем из уравнения

находим y k-кратным интегрированием.

Пример 5.2. Решить уравнение.

Решение.Полагая, получаем, откуда

,.

Последовательно интегрируя, получаем:

,

3.Уравнение не содержит независимой переменной:

.

Подстановка позволяет понизить прядок уравнения на единицу. Производныевыражаются через производные функции.

,

и т.д.

Подстановка этих выражений в уравнение приводит к понижению порядка на единицу.

Пример 5.3.Решить уравнение.

Решение.Уравнение не содержит независимой переменнойx. Полагая,, получаем уравнение

Подстановкой оно сводится к линейному уравнению

,

общее решение которого

.

После обратной замены имеем

а после разделения переменных

, .

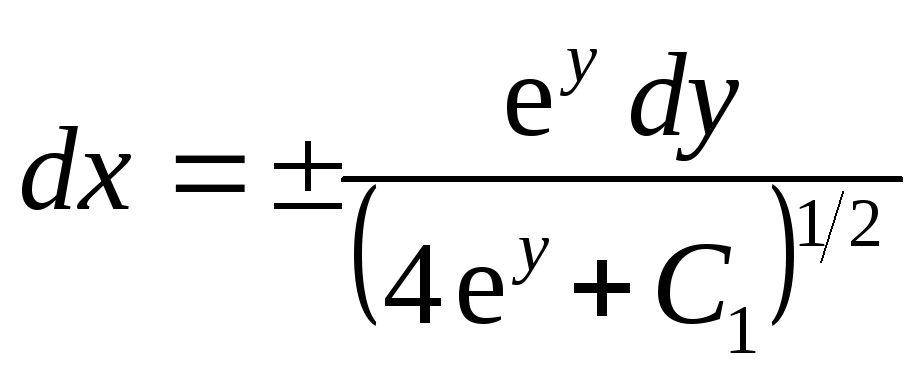Проинтегрировав, получаем

откуда

.

Это общий интеграл данного уравнения.

4209.Решить уравнение.

Решение.Интегрируя уравнение последовательно три раза, получим:

,,

,

Это и есть общее решение исходного уравнения.

4163.Решить уравнение.

Решение.Уравнение не содержит искомой функции, замена переменнойпозволит понизить порядок уравнения и оно примет вид

или,

откуда

.

Проинтегрировав, получим

,.

Учтем, что , и продолжим интегрирование:

и

.

Это есть общее решение.

4171.Решить уравнение.

Решение.Уравнение не содержит переменной. Будем считать независимой переменной, а в качестве искомой функции примем

, тогда

Подставив всё в уравнение, получим:

откуда.

После интегрирования:

и наконец,

.

Контрольные вопросы.

1. Запишите общий вид дифференциального уравнения -го порядка.

2. Что называется общим решением дифференциального уравнения -го порядка?

3. Перечислите три вида дифференциальных уравнений, допускающих понижение порядка.

Занятие 6. Линейные дифференциальные уравнения.

Упражнения на занятии: 4251, 4253, 4255, 4257, 4263, 4276(1-4, 5, 6), 4279(1-6).

На дом. № 4252, 4254, 4256, 4262, 4275(1 5, 8, 11), 4278(1–6).

Линейным дифференциальным уравнениемпорядкаnназывается уравнение вида

. (6.1)

Отличительной чертой линейного уравнения является то, что искомая функция и все её производные входят в это уравнение линейно. Предполагается, что заданные функции инепрерывны в некотором промежутке.

Зaдача Коши для этого уравнения при сделанных предположениях имеет единственное решение, если принадлежит промежутку.

Если в уравнении (6.1) правая часть тождественно равна нулю, то уравнение называетсялинейным однородным(ЛОДУ), в противном случае –линейным неоднородным(ЛНДУ). Линейное однородное дифференциальное уравнение имеет вид:

. (6.2)

Если функции иявляются решениями линейного однородного уравнения (6.2), то, где– произвольная постоянная, и сумматакже являются решениями этого дифференциального уравнения.

Если функции являются решениями дифференциального уравнения (6.2), то их линейная комбинация

, (6.3)

где – произвольные постоянные, также является решением уравнения (6.2).

Функции называютсялинейно независимымив промежутке, если равенство

, (6.4)

где – постоянные, имеет место только тогда, когда равны нулю все коэффициенты.

Если же равенство (6.4) имеет место на при условии, что хотя бы один коэффициентотличен от нуля, то система функций–линейно зависимая.

Если функцийявляются решениями линейного однородного дифференциального уравнения (6.2) и линейно независимы на промежутке, то общее решение уравнения (6.2) имеет вид:

, (6.5)

где – произвольные постоянные.

Система из любых nлинейно независимых решений ЛОДУ (6.2) называетсяфундаментальной системой решений (ФСР)этого уравнения.

Если функции определены ираз дифференцируемы на промежутке, то может быть построен следующий определительn-го порядка:

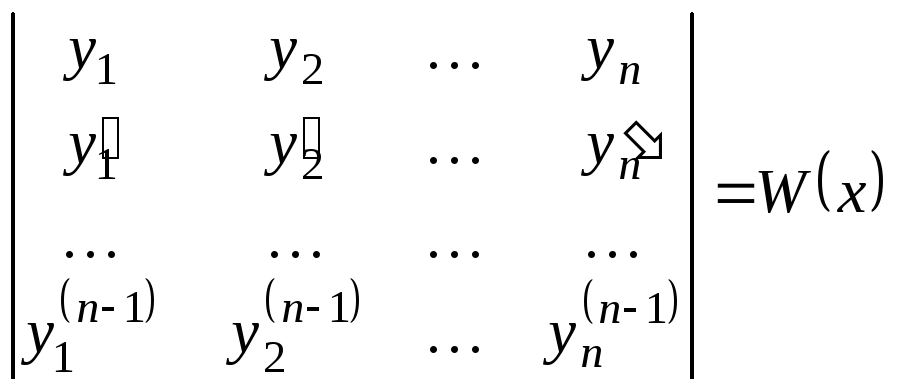. (6.6)

Это определитель Вронского (или вронскиан)для данной системы функций. С его помощью устанавливается, является ли система решений уравнения линейно независимой. Применение вронскиана основано на следующих теоремаx.

Теорема 1.Если функциилинейно зависимы, то вронскиан системы тождественно равен нулю.

Теорема 2.Если функции– линейно независимые решения, удовлетворяющие некоторому ЛОДУn-го порядка с непрерывными коэффициентами, то вронскиан такой системы не обращается в нуль ни в одной точке промежутка.

Таким образом, чтобы проверить линейную независимость решений ЛОДУ (6.2), надо составить определитель Вронскогои убедиться, что при любом значениииз промежуткаон не равен нулю.

Пример 6.1.Найти определитель Вронского для системы функций, где числаk, l, mразличны. Заметим, что эти функции являются решениями такого ЛОДУ:

.

W(x)=

=

.

Это доказывает линейную независимость функций

Линейные однородные уравнения с постоянными коэффициентами n - го порядка. Общий вид уравнения:

, (6.7)

где - вещественные постоянные,.

Решение уравнения (6.7) ищем в виде экспоненты . Наводящие соображения: поскольку уравнение представляет собой тождественно равную нулю линейную комбинацию функцииyи её производных, следует искать решение в виде функции, не меняющей свой вид при дифференцировании.

Подставив в уравнение (6.7), получим

.

Здесь , следовательно,

. (6.8)

Это характеристическое уравнениедля (6.7); пусть– его корни. Возможны четыре случая.

1. Корни вещественные и различные. Тогда фундаментальная система решений уравнения (6.7) имеет вид:(каждому корню соответствует одна функция в ФСР), а общее решение уравнения (6.7)

,,.

2.Корни характеристического уравнения вещественные, среди них есть кратные. Пусть, а остальные корни различные. Тогда фундаментальная система решений имеет вид:

Корню кратностиkсоответствуетkфункций в ФСР, а общее решение уравнения:

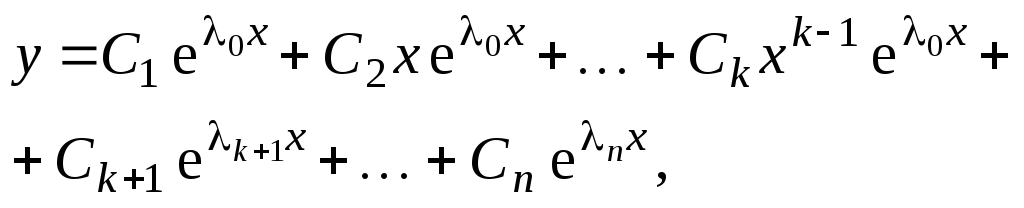
где ,– произвольные коэффициенты.

Пример 6.2.Решить уравнение.

Решениеищем в виде. Подставив в уравнение, получим характеристическое уравнение:

,

или

.

Корни – действительные, один из корней двукратный, поэтому общее решение:

.

3.Среди корней характеристического уравнения eсть комплексные однократные, например, а– действительные различные. Фундаментальная система решений в этом случае имеет вид:

(паре комлексно-сопряженных корней соответствует пара функций в ФСР), а общее решение

4.Среди корней характеристического уравнения есть комплексно-сопряженныеикратностиk, а– действительные различные. В этом случае фундаментальная система решений имеет вид:

а общее решение:

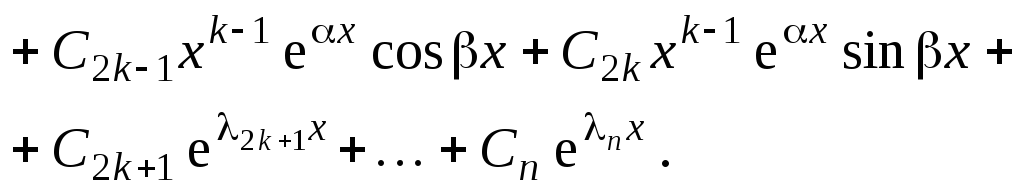
Пример 6.3.Решить уравнение

.

Решениеищем в виде экспоненты. Подставив в уравнение, получим характеристическое уравнение:

или.

Оно имеет двукратные комплексные корни:

и.

Общее решение уравнения имеет вид:

Линейные неоднородные уравнения с постоянными коэффициентами n-го порядка.

Пусть дано дифференциальное уравнение:

(6.9)

с постоянными коэффициентами и.

Теорема. Общее решение неоднородного уравнения (6.9) равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.

Отыскание общего решения соответствующего однородного уравнения осуществляется по правилам, изложенным выше. Частное решение неоднородного уравнения для случая правых частей специального вида находится методом подбора, или иначе, методом неопределенных коэффициентов.

Общий вид правой части уравнения (6.9), при котором применим метод неопределенных коэффициентов, следующий:

. (6.10)

Здесь и– многочлены степениlиmсоответственно. В этом случае частное решение уравнения (6.9) ищем в следующем виде:

, (6.11)

где , и – многочлены отстепениk общего вида с неопределенными коэффициентами, а– кратность корня характеристического уравнения. (Еслине является корнем, то.)

Пример 6.4.Решение уравнения.

Решение.Сначала найдем общее решение соответствующего однородного уравнения

.

Его характеристическое уравнение:

имеет корни и. Общее решение однородного уравнения:

.

Теперь нужно найти частное решение неоднородного уравнения. Сравнивая его правую часть с формулой (6.10), видим, что , . Числокорнем характеристического уравнения не является, следовательно,.PиQ– многочлены нулевой степени, следовательно, частное решение будем искать в виде

.

Удобно расположить в столбик, написав слева значения коэффициентов из исходного уравнения:

Сложив всё, получим:

,

,

а общее решение неоднородного уравнения

Пример 6.5. Решить уравнение

Решение.Однородное уравнение имеет вид

его характеристическое уравнение:

корни.

Общее решение:

Чтобы правильно выбрать вид частного решения неоднородного уравнения согласно формуле (6.11), сравним правую часть уравнения с общим её представлением по формуле (6.10). Очевидно, является однократным корнем характеристического уравнения, поэтому. (В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.) Кроме того, замечаем, что степени многочленовPиQ– нулевые. Вид частного решения:

.

Подставим в исходное уравнение:

В итоге

;

, .

Общее решение:

4275 (1-6).Решить уравнение

,

где равна: