17. 4.1. Условие задания № 4

Дана таблично заданная функция - пары точек (x_i,y_i):

для которых в Excel необходимо провести 2 вида аппроксимации: линейную и полином 5-й степени. Оба графика построить на одной координатной плоскости. В обоих случаях определить сумму квадратов отклонений для узловых точек.

18. 4.2. Решение задания № 4

1. Запишем в столбец А значения Х, а в столбец В значения У. На основе такой таблицы построим точечную диаграмму с маркерами (рис. 1).

Рис. 1. Точечная диаграмма с маркерами

Вызовем контекстное меню для одной из точек на графике и выберем пункт «Добавить линию тренда...». Для начала проведем линейную аппроксимацию. В параметрах линии тренда выберем «линейная», настроим тип и толщину линии, а также отметим «показывать уравнение на диаграмме». Так же добавим еще одну линию тренда «Полиномиальная», указав степень равную 5 и отметив «Показывать уравнение на диаграмме» (рис. 2).

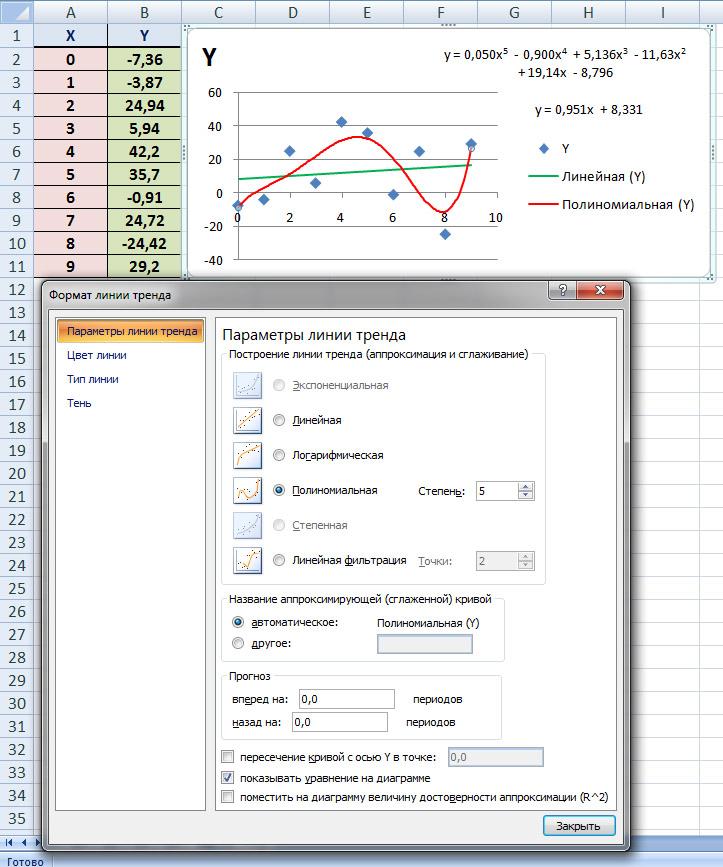
Рис. 2. Добавление линии тренда

Таким образом, получили следующие аппроксимирующие функции:

Для линейной функции: y = 0,951x + 8,331

Для полинома 5 степени: y = 0,050x⁵ - 0,900x⁴ + 5,136x³ - 11,63x² + 19,14x - 8,796

На основе этих формул заполним:

столбец С (для линейной функции):

=A_i*0,951+8,331

столбец Е (для полинома 5 степени):

=0,05*A_i^5-0,9*A_i^4+5,136*A_i^3-11,63*A_i^2+19,4*A_i-8,796

Аппроксимация набора данных функцией более точна, если сумма квадратов отклонений меньше. Поэтому для сравнения двух функций заполним еще две колонки квадратов отклонений:

для линейной функции столбец D =(C_i-B_i)^2

для полинома 5 степени столбец А =(E_i-B_i)^2

а также ячейки D12 и А12, вычисляющие сумму соответствующих столбцов с квадратами отклонений (рис. 3).

Рис. 3. Вычисление сумм квадратов отклонений

Очевидно, что сумма квадратов отклонений линейной функции (4176,78) почти вдвое выше, чем сумма квадратов отклонений полинома 5-й степени (2034,76). Следовательно, аппроксимация полиномом 5-й степени более точна, чем линейной функцией.