ЛИВС Курсовая / LIVS_kursach_1

«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

им.В. И. Ульянова (Ленина)» (СПбГЭТУ)

Кафедра ИИСТ

Отчёт по курсовому проекту

по дисциплине: Локальные ИВС.

Часть 1. «Разработка канала для измерения температуры»

Цель работы: разработать измерительный канал для измерения температуры.

Задание:

1. Диапазон изменения: – 100,0, …, +150,0 ^оС.

2. Погрешность измерения: γ=1,0%.

3. Датчик: терморезистор 500П

R_Т = R₀ [1 +аТ + вТ² +с(T – 100)³], Ом,

где R₀ = 500 Ом, а = 0,00397, в = – 5,85·10^-7 , с = 0 при Т>0^о , с = 4.22·10^-12 при Т<0.

4. Результат отобразить на цифровом индикаторе в десятичной системе исчисления.

Структурная схема канала:

где, ПИП – первичный измерительный преобразователь(датчик), ВИП – вторичный измерительный преобразователь(стабилизатор тока), НП – нормирующий преобразователь,

АЦП – аналогово-цифровой преобразователь, МП – масштабный преобразователь,

ЦП – цифровой преобразователь(обратная функция преобразования), И – индикатор(вывод результата).

1. Расчет функциональных блоков.

Определение функций преобразования:

В данной работе для расчет функциональных блоков была использована среда MatLAB.

Листинг М-файла:

Функциональный блок ПИП:

clear all;

T=-100:1:150;

R0=500;

a=0.00397;

b=-5.85e-7;

c=4.22e-12;

if T<0

Rt=R0*(1+a*T+b*T.^2+c*(T-100).^3);

else

Rt=R0*(1+a*T+b*T.^2);

end

figure(2);

plot(T,Rt), xlabel('T, ^0C'), ylabel('Rt, Om'), title({'График прямого преобразования';'R(T)'});

grid on

График прямого преобразования(рис.1).

Рисунок 1

Функциональный блок ВИП:

I0=10e-3;

Ur=Rt*I0;%напряжение на выходе ВИП

figure;

subplot(1,2,1);

plot(Rt,Ur), xlabel('Rt, Om'), ylabel('Ur, B'), title('Ur(Rt)');

grid on

График вторичного преобразования(рис.2а).

Функциональный блок НП:

k=10/max(Ur-min(Ur)); коэффициент нормирования

Un=(Ur-min(Ur))*k;%нормированное напряжение

subplot(1,2,2);

plot(Ur,Un), xlabel('Ur, B'), ylabel('Un, B'), title('Un(Ur)');

grid on

График нормирующего преобразования(рис.2б).

(а) (б)

Рисунок 2

Функциональный блок АЦП:

N=Un/(10/256);

s=N/256;

figure;

plot(Un,s), xlabel('Un, B'), ylabel('s'), title('s(Un)');

grid on

График преобразования на выходе АЦП(рис.3).

Рисунок 3

Функциональный блок МП:

Nt=s*(150+100)-100;% функция масштабирующего преобразования

figure;

plot(s,Nt), xlabel('s'), ylabel('Nt'), title('Nt(s)');

grid on

График масштабирующего преобразования рис.4).

Рисунок 4

Функциональный блок ЦП:

figure;

plot(Nt,T), xlabel('Nt'), ylabel('T, ^0C'), title('T(Nt)');

grid on

save('ObrPrejbrazovanie.mat','Nt');

График обратного преобразования(рис.5).

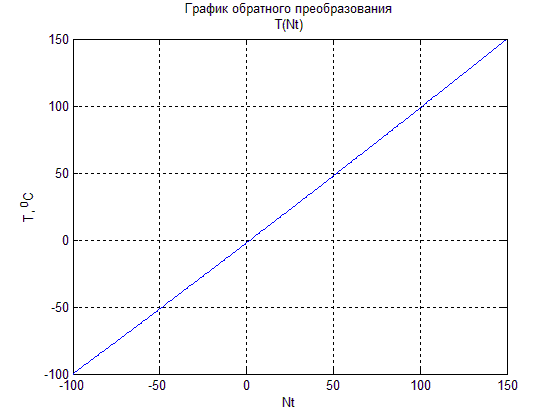
Рисунок 5

Аппроксимация обратной функции преобразования.

Следующий этап работы получение аналитического выражения для обратной функции преобразования. Для этого необходимо провести аппроксимацию.

Аппроксимация проводилась в среде MatLab, по данным записанным в файле ObrPrejbrazovanie.mat.

Было принято решение провести аппроксимацию полиномом 2го порядка вида:

Листинг М-файла.

clear all;

load ObrPrejbrazovanie.mat

T=-100:150;

p=polyfit(Nt,T,2);

X=polyval(p,Nt);

dT=max(X-T);

plot(Nt,T,['c']),grid on, xlabel('Nt'), ylabel('T,^0C');

title('График функции обратного преобразования построенного по точкам');

figure;

plot(Nt,X,['-' 'r']);grid on, xlabel('Nt'), ylabel('T,^0C');

title('График аппроксимации функции обратного преобразования');

axis([-100,150,-100,150]);

Рисунок 6

Рисунок 7.

далее приведем рассчитанные коэффициенты аппроксимации и значение максимальной погрешности.

a₂=1,48∙10^-4; a₁=0,99; a₀=-2,220; T_апр=0,0336;

тогда функция аппроксимации обратного преобразования:

2. Метрологический расчет.

Определение требований к реализации каждого блока измерительного канала, выбор разрядности АЦП.

Формулы абсолютной и приведенной погрешности:

(1)

(2)

Согласно условию задания погрешность аппроксимации не должна превышать 10% от абсолютной погрешности измерительного канала.

Абсолютная погрешность измерительного канала равна:

; (3)

максимальное значение погрешности аппроксимации равно: T_апр=0.0336 ºС.

T_апр=0.036 ºС < Т∙10%=0,25 ºС (4)

Неравенство(4) показывает что функция аппроксимации обратного преобразования удовлетворяет требованиям по точности.

Погрешность обратного преобразования равна погрешности аппроксимации T_апр.

Получается что на оставшиеся блоки измерительного канала выделяется абсолютная и приведенная погрешности:

(5)

(6)

Где S – диапазон измеряемой величины.

Пусть на вход АЦП поступает аналоговый сигнал с некоторой погрешностью γ_a.

АЦП за счет квантования аналогового сигнала вносит дополнительную погрешность γ_кв.

При аддитивном характере составляющих погрешности γ_a и γ_кв результирующая погрешность будет определяться как γ_z = γ_a + γ_кв. (7)

По условию задания погрешность измерительного канала мы делим поровну между цифровой и аналоговой частью. В связи с тем что погрешность масштабирующего преобразования очень мала, мы ей пренебрегаем и считаем равной нулю. В результате выше сказанного мы получаем что γ_a = γ_кв.

Тогда (8)

Отсюда абсолютные погрешности аналоговой и цифровой части и их СКО будут равны:

(9)

(10)

(11)

(12)

Где S_а - диапазон значений на входе ацп(0;10) ; S_кв – диапазон значений на выходе ацп(0;1)

Погрешность квантования распределена по равномерному закону распределения.

Погрешность аналоговой части распределена по нормальному закону распределения.

Предъявление требований к аналоговым элементам.

Аналоговая часть состоит из следующих функциональных блоков: датчик(ПИП), источник тока(ВИП), нормирующий преобразователь(НП). Распределим погрешность аналоговой части поровну на каждый из этих блоков. Т.е.

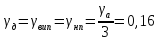(13)

Тогда абсолютная погрешность функциональных блоков будут равны:

(14)

(15)

(16)

Где S_д - диапазон значений на выходе датчика; S_вип - диапазон значений на выходе ВИП;

S_нп - диапазон значений на выходе нормирующего преобразования.

Выбор разрядности АЦП

шаг квантования который мы берем равным погрешности квантования вычисляется по формуле:

Δ_кв=S_кв/Nmax= S_кв/(2ⁿ-1) (17)

Выведем из формулу(17) разрядность, мы получаем что она равна:

(18)

поскольку в общем случае n* не является целым числом, для обеспечения заданной точности необходимо взять в качестве количества разрядов АЦП ближайшее большое целое

n= Е(n*)+1=8, (19)

где Е – оператор выделения целой части от числа

разрядность АЦП .

Вывод:

В данной работе были получены данные необходимые для построения измерительного канала. Получена обратная функция преобразования, а так же ее аппроксимация. Был произведен выбор разрядности АЦП n=8. Был выполнен метрологический расчет функциональных блоков.