
- •Пример выполнения типового задания
- •1. Дифференциальные уравнения первого порядка. Основные понятия и определения.
- •3. Д.У. Второго порядка. Основные понятия и определения
- •6. Линейные неоднородные уравнения второго порядка
- •7. Линейные однородные системы с постоянными коэффициентами. Метод Эйлера.
- •8. Линейные однородные системы с постоянными коэффициентами. Операционный метод.
- •9. Пример выполнения типового расчета
8. Линейные однородные системы с постоянными коэффициентами. Операционный метод.
Полное
изложение метода дано в учебнике [1]. В
основе метода преобразование Лапласа
функции
![]()
 ,
,
где
![]() .
Функция
.
Функция
![]() называется оригиналом,
называется оригиналом,
![]() ее изображением. Принято обозначение
ее изображением. Принято обозначение
![]()
![]() .
В таблице 3 приведены изображения
основных элементарных функций. Основные
теоремы операционного исчисления см.
в учебнике [1].
.
В таблице 3 приведены изображения
основных элементарных функций. Основные
теоремы операционного исчисления см.
в учебнике [1].
Таблица 3
|
№ |
Оригинал
|
Изображение
|
№ |
Оригинал
|
Изображение
|
|
1 |
|
|
5 |
|
|
|
2 |
|
|
6 |
|
|
|
3 |
|
|
7 |
|
|
|
4 |
|
|
8 |
|
|
9. Пример выполнения типового расчета
Задания 1 8, 10 13. Найти общие решения (общие интегралы) дифференциальных уравнений. Где указано, найти решение задачи Коши.
Задание
1.
![]() .
.
Решение.
Это уравнение простейшего типа. Его
общее решение имеет вид (2.2):
![]()
Под знаком интеграла неправильная дробно-рациональная функция. Выделяем целую часть
![]() .
.
Интегрируя, получим
![]()
Ответ:
![]()
Задание
2.
![]()
Решение. Это уравнение с разделяющимися переменными (см. (2.4.)). Запишем уравнение в дифференциальной форме:
![]()
Разделив
обе части уравнения на
![]() ,
получим уравнение с разделенными
переменными
,
получим уравнение с разделенными
переменными
![]()
Общий интеграл уравнения (см. (2.5)) имеет вид:
![]()
Ответ:
![]()
![]()
Задание
3.
Найти решение задачи Коши:
![]() .
.
Решение.
Найдем сначала общее решение уравнения.
Это линейное уравнение (см.(2.7.)). Решение
уравнения ищем в виде:
![]()
![]()
![]() .
Уравнение примет вид
.
Уравнение примет вид
![]()
Выберем
функцию
![]() так, чтобы
так, чтобы
![]() тогда приходим к системе уравнений
(см. (2.8)):
тогда приходим к системе уравнений
(см. (2.8)):

Уравнение (9.1) УРП. Разделим переменные
![]()
Выберем одно решение этого уравнения (С=0):
![]()
Находим решение уравнения (7.2):
![]()
Общее
решение уравнения имеет вид:
![]() .
.
Найдем
решение задачи Коши. Найдем значение
постоянной С из условия: при
![]() .
Имеем
.
Имеем
![]() .
.
Ответ.
Решение задачи Коши:
![]() .
.
Задание
4.
![]() .
.
Решение. Это уравнение Бернулли (см.п. 2.6.). Решение ищем методом Бернулли:
![]() .
.
Уравнение примет вид:
![]()
Выберем
функцию
![]() так, чтобы
так, чтобы
![]() .
Приходим к системе уравнений
.
Приходим к системе уравнений

Найдем какое-нибудь решение уравнения (7.3).
![]()
Тогда
![]() .
.
Уравнение (7.4) примет вид
![]()
Общий
интеграл уравнения:
![]() .
Отсюда
.
Отсюда
![]()
Ответ.
Общее решение:
![]()
Задание
5.
![]() .
.
Решение.
Правая часть этого уравнения есть
функция
![]() .
Следовательно, это однородное уравнение
(см.п. 2.4). Делаем замену
.
Следовательно, это однородное уравнение
(см.п. 2.4). Делаем замену
![]() .
Тогда
.
Тогда
![]()
Уравнение примет вид
![]()
Это УРП. Разделяем переменные
![]()
Отсюда
![]()
Подставив
![]() ,
получим общий интеграл уравнения.
,
получим общий интеграл уравнения.
Ответ.
![]()
Задание
6.
![]()
Решение.
Обозначим
![]() .
Тогда
.
Тогда
![]() .
.
Следовательно,
это уравнение в полных дифференциалах.
Общий интеграл уравнения (см. п. 2.7):
![]() ,
,
где
функция
![]() находится из системы уравнений (2.13):
находится из системы уравнений (2.13):

Интегрируем уравнение (7.5):
![]() ,
(9.7)
,
(9.7)
где
![]() неизвестная
дифференцируемая функция аргумента
неизвестная
дифференцируемая функция аргумента
![]() .
.
Подставим (7.7) в уравнение (7.6):
![]()
Отсюда
![]() .
.
Согласно формуле (7.7)
![]()
Ответ.
Общий интеграл
![]()
Задание
7.
![]()
Решение.
Это уравнение второго порядка и явно
не содержит функции
![]() .
Согласно пункту (4.1) вводим новую функцию
.
Согласно пункту (4.1) вводим новую функцию
![]() и приходим к системе уравнений
и приходим к системе уравнений

Уравнение
(7.8)
УРП. Разделяем переменные (положить
![]() )
)
![]() .
.
Отсюда
(учесть, что
![]() )
получим
)
получим
![]()
Подставляем
![]() в уравнение (9.9). Оно простейшего типа.
в уравнение (9.9). Оно простейшего типа.
Согласно (2.1)
![]() .
.
Ответ.
Общее решение
![]() .
.
Задание
8.
![]()
Решение.
Дифференциальное уравнение второго
порядка не содержит явно переменной
«![]() ».
Согласно (4.2) считаем
».
Согласно (4.2) считаем
![]() переменной интегрирования и полагаем
переменной интегрирования и полагаем
![]() .
.
Приходим к системе уравнений
![]()

Разделяем переменные в уравнении (7.10):
![]()
Отсюда
![]() .
Уравнение (7.11) примет вид
.
Уравнение (7.11) примет вид
![]()
Это уравнение с разделяющимися переменными (УРП):
![]()
Ответ.
Общий интеграл уравнения:
![]() .
.
Задание
9.
Даны корни характеристического уравнения
ЛОУ второго порядка с постоянными
коэффициентами:
![]() .
Правая часть ЛНУ:
.
Правая часть ЛНУ:
![]() Написать частное решение ЛНУ (коэффициенты
не находить).
Написать частное решение ЛНУ (коэффициенты
не находить).
Решение.
Правая часть уравнения
сумма трех функций специального вида:
![]() ,
где
,
где
1)
![]() многочлен
второго порядка,
многочлен
второго порядка,
![]() ;
;
2)
![]()
3)
![]() .
.
Согласно
таблице 2 частное решение ЛНУ,
соответствующее
![]() ,
имеет вид:
,
имеет вид:
![]() ;
функции
;
функции
![]()
![]() ;
функции
;
функции
![]()
![]() .
.
Частное
решение ЛНУ с функцией
![]() в правой части имеет вид:
в правой части имеет вид:
![]()
![]() +
+![]()
![]() .
.
Коэффициенты
![]() неизвестны.
неизвестны.
Ответ.
![]()
Задание
10.
![]() .
.
Решение. Это ЛНУ второго порядка с правой частью специального вида (таб.2, п.3). Находим общее решение однородного уравнения
![]()
Характеристическое уравнение
![]() .
.
Его
корни
![]() .
.
Следовательно (см. таб.1), общее решение ЛОУ имеет вид
![]()
В
правой части ЛНУ многочлен второго
порядка, кроме того
![]()
Частное решение ЛНУ (см.табл.2, п.3) ищем в виде
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
Подставив
в исходное уравнение
![]() ,
получим
,
получим
![]()
![]()
Приравниваем
коэффициенты при одинаковых степенях
![]() справа
и слева:
справа
и слева:

Частное решение имеет вид
![]()
Общее решение имеет вид
![]()
![]()
![]()
Ответ.
![]()
![]()
Задание
11.
![]()
Решение. Это ЛНУ второго порядка с правой частью специального вида (таб.2, п.3). Находим общее решение однородного уравнения
![]()
Характеристическое уравнение
![]()
имеет
корни
![]() .
Общее решение ЛОУ (см. табл. 1)
.
Общее решение ЛОУ (см. табл. 1)
![]()
Найдем частное решение ЛНУ. Его правая часть специального вида
![]()
Частное решение ищем в виде
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Подставив
в исходное уравнение
![]() ,
получим
,
получим
![]()
![]()
Частное
решение ЛНУ имеет вид
![]() ,
общее решение
,
общее решение
![]()
Ответ.
![]()
Задание
12.
![]()
Решение. Это ЛНУ второго порядка с правой частью нестандартного вида. Находим фундаментальную систему решений ЛОУ:
![]()
Его характеристическое уравнение
![]()
Корни
уравнения
![]() .
.
Фундаментальная система решений (см.табл.1)
![]()
Тогда
![]()
Решение ЛНУ ищется в виде
![]() (9.12)
(9.12)
Система
уравнений (6.6) для определения
![]() примет вид
примет вид

Используем формулы Крамера. Определитель системы
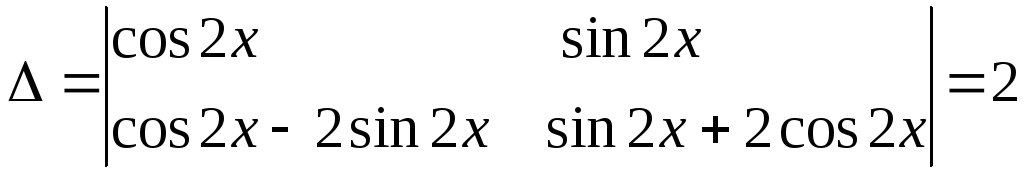 (проверьте!)
(проверьте!)
Вспомогательные определители


Итак,
![]()
Тогда
![]()
![]()
Здесь
![]() произвольные
постоянные.
произвольные
постоянные.
Подставляя
![]() в
формулу (9.12) получим общее решение ЛНУ.
в
формулу (9.12) получим общее решение ЛНУ.
Ответ.
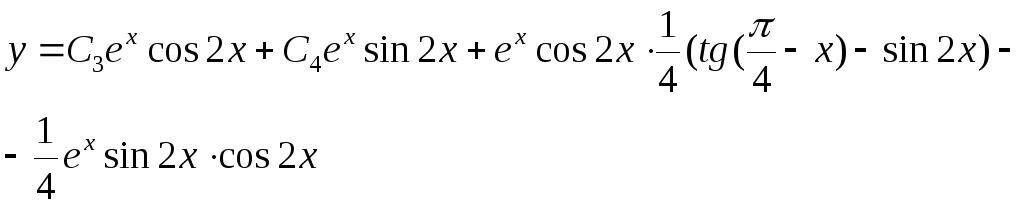
Задание
13.
Найти решение задачи Коши:
![]() ,
(9.13)
,
(9.13)
![]() (9.14)
(9.14)
Решение. Найдем общее решение ЛНУ (9.13). Его правая часть специального вида. Используем метод неопределенных коэффициентов.
Характеристическое уравнение
![]()
Общее решение однородного уравнения (см. табл.1)
![]() (9.15)
(9.15)
Правая
часть ЛНУ
![]() ,
,
![]()
Следовательно, (см. табл.2), частное решение надо искать в виде:
![]() .
.
Дифференцируем
![]() и подставляем в уравнение (9.13):
и подставляем в уравнение (9.13):
![]()
![]() ,
,
(7.13):
![]() .
.
Приравниваем
коэффициенты при
![]() и при
и при
![]() справа и слева
справа и слева

Частное
решение уравнения (7.13):
![]() .
.
Общее решение уравнения (7.13):
![]() (9.16)
(9.16)
Отсюда
![]() (9.17)
(9.17)
Найдем решение задачи Коши. Подставим в (7.16) и (7.17)
![]()

![]()
Ответ. Решение задачи Коши
![]()
Задание 14. Найти решение задачи Коши системы тремя методами: методом исключения, методом Эйлера, операторным методом.
 ,
,
![]() .
(9.18)
.
(9.18)
Решение. Подробное изложение данной темы см. в [1].
Метод исключения.
Дифференцируем
по аргументу «![]() »
одно из уравнений системы, например,
первое:
»
одно из уравнений системы, например,
первое:
![]()
Подставляем
![]() из второго уравнения
из второго уравнения
![]() (9.19)
(9.19)
Из первого уравнения находим
![]()
и подставляем его в уравнение (9.19)
![]() .
.
Т.о., мы приходим к системе уравнений

Первое уравнение системы ЛОУ второго порядка с постоянными коэффициентами. Его характеристическое уравнение
![]()
Общее решение (см. табл. 1) имеет вид
![]() (9.20)
(9.20)
Тогда
![]() .
Второе уравнение системы дает
.
Второе уравнение системы дает
![]() (9.21)
(9.21)
В
уравнениях (7.20) и (7.21) положим
![]() :
:
 .
.
Подставляем
![]()
![]() в уравнения (7.20) и (7.21) и получаем решение
задачи Коши.
в уравнения (7.20) и (7.21) и получаем решение
задачи Коши.
Ответ.
![]() ,
,
![]()
Метод Эйлера. Характеристическое уравнение (9.3) системы имеет вид
 .
.
Отсюда
![]()
Числа
![]() ,
соответствующие собственному числу
,
соответствующие собственному числу
![]() находим из системы (см. (7.4))
находим из системы (см. (7.4))
 .
.
Аналогично,
числа
![]() ,
соответствующие собственному числу
,
соответствующие собственному числу
![]() находим из системы (см. (7.4))
находим из системы (см. (7.4))
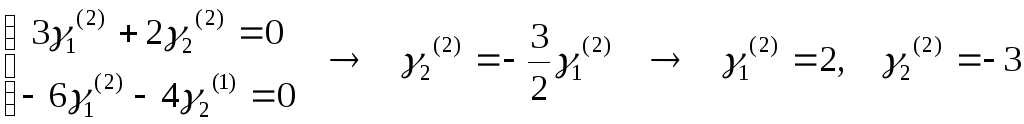 .
.
Два линейно независимых частных решений системы имеют вид
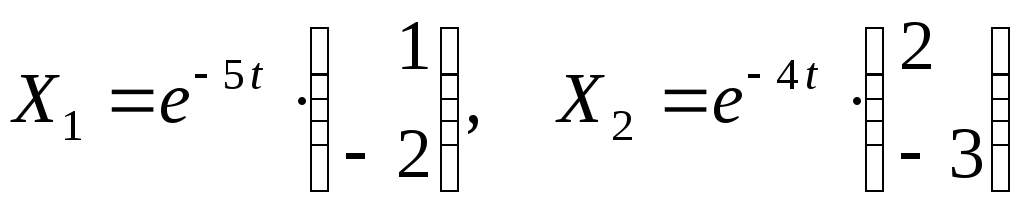
Общее решение
 .
.
В развернутом виде общее решение системы
![]()
![]()
Положим
![]() .
Тогда
.
Тогда

Решение задачи Коши имеет вид
![]()
![]()
Получен тот же результат, что и методом исключения.
Операционный метод. Обозначим изображения неизвестных функций
![]()
![]()
![]()
![]()
Тогда изображения производных (см.п.8)
![]()
![]()
![]()
![]()
Изображение системы (7.18) имеет вид

Решение системы находим по формулам Крамера.
Определитель
системы
 ,
,


Операторное решение системы уравнений (7.8) имеет вид
![]()
![]()
По таблице 3 изображений и оригиналов находим
![]()
![]() ,
,
![]()
![]()
Тогда решение задачи Коши (7.8) имеет вид
![]() ,
,
![]() ,
,
что совпадает с решением по другим методам.
Ответ.
![]() ,
,
![]() .
.
Задание
15.
Тело массой
![]() подброшено вертикально вверх с поверхности
планеты (
подброшено вертикально вверх с поверхности
планеты (![]() )
со скоростью
)
со скоростью
![]() и замедляет движение под действием веса
тела и силы сопротивления среды:
и замедляет движение под действием веса
тела и силы сопротивления среды:
![]() где
где
![]() расстояние
от тела до начала координат в момент
времени
расстояние
от тела до начала координат в момент
времени
![]() Найти закон движения тела и время первой
остановки тела.
Найти закон движения тела и время первой
остановки тела.
Решение.
В заданиях 15 используется второй закон Ньютона:
![]() ,
где
,
где
![]() вектор
ускорения,
вектор
ускорения,
![]() масса
тела,
масса
тела,
![]() суммарный вектор действующих сил.
суммарный вектор действующих сил.
Если
движение прямолинейное, ось
![]() направлена вертикально вверх и
направлена вертикально вверх и
![]() расстояние
от начала координат до движущегося тела
в момент времени
расстояние
от начала координат до движущегося тела
в момент времени
![]() ,
то уравнение движения согласно условию
задачи примет вид:
,
то уравнение движения согласно условию
задачи примет вид:
![]()
Это ЛНУ с постоянными коэффициентами и правой частью специального вида. Характеристическое уравнение имеет вид
![]()
Общее решение соответствующего однородного уравнения имеет вид
![]()
Частное решение (см. табл.2) ищем в виде
![]() .
.
Для
определения
![]() получаем уравнение:
получаем уравнение:
![]()
![]()
Общее решение ЛНУ
![]()
Начальные
условия:
![]() (в начальный момент времени тело
находилось на поверхности планеты
в начале координат);
(в начальный момент времени тело
находилось на поверхности планеты
в начале координат);
![]() .
.
Для
определения
![]() имеет систему уравнений
имеет систему уравнений
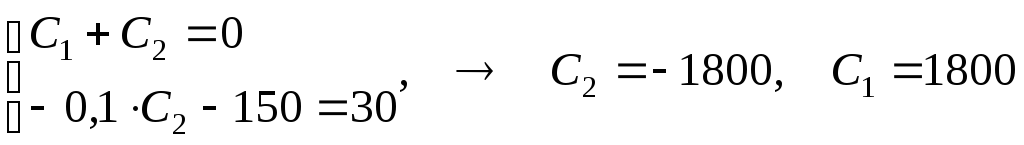
Закон
движения тела:
![]()
Скорость
тела:
![]() .
.
Время первой остановки тела (скорость равна нулю):
![]()
