12

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено

на заседании кафедры физики

20 мая 2011 г.

Методические указания

к лабораторной работе № 10

«Изучение колебаний пружинного маятника»

(для бакалавриата всех профилей)

Ростов-на-Дону

2011

УДК 531.383

Методические указания к лабораторной работе № 10 «Изучение колебаний пружинного маятника». – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 11 с.

Содержатся краткая теория метода, порядок выполнения лабораторной работы, требования техники безопасности, требования к оформлению результатов, а также перечень контрольных вопросов и тестов.

Предназначены для выполнения лабораторной работы по программе курса физики для студентов бакалавриата очной и заочной форм обучения всех профилей по направлениям:

270800 «Строительство»

270200 «Реконструкция и реставрация архитектурного наследия»

280700 «Техносферная безопасность»

190700 «Технология транспортных процессов»

190600 «Эксплуатация транспортно-технологических машин и комплексов»

230400 «Информационные системы и технологии»

230700 «Прикладная информатика»

120700 «Землеустройство и кадастр»

261400 «Технология художественной обработки материалов»

221700 «Стандартизация и метрология»

100800 «Товароведение»

Электронная версия находится в библиотеке, ауд. 224.

УДК 531.383

Составители: проф. Н.Н. Харабаев,

проф. А.Н. Павлов

Рецензент доц. Ю.И. Гольцов

Редактор н.Е. Гладких

Доп. план 2011 г., поз. 125

Подписано в печать 22.06.11 Формат 60х84 ¹/₁₆. Бумага писчая. Ризограф. Уч.-изд. л 0,7.

Тираж 100 экз. Заказ 329.

Редакционно-издательский центр

Ростовского государственного строительного университета.

334022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2011

Лабораторная работа № 10

ИЗУЧЕНИЕ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА

Цель работы: изучение основных закономерностей упругих колебаний на примере пружинного маятника.

Приборы и принадлежности: универсальный штатив для крепления пружины с отсчетной линейкой, пружина, грузы (3 шт.), секундомер.

Краткая теория эксперимента

П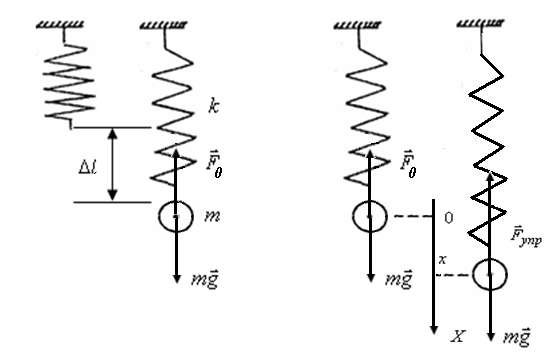римером свободных незатухающих гармонических колебаний могут служить колебания груза, подвешенного на абсолютно упругой пружине и совершающего колебания под действием упругой силы.

Рис.1 Рис.2

Рассмотрим груз массой m, подвешенный на пружине жесткостью k (рис.1). Под действием этого неподвижно висящего груза пружина оказывается растянутой на величину l (рис.1, l – статическое растяжение пружины).

При статическом равновесии в нагруженном состоянии (рис.1) сила тяжести груза уравновешивается силой упругости растянутой пружины , т. е. для статического равновесия:

.

По закону Гука величина силы упругости растянутой или сжатой пружины прямо пропорциональна величине растяжения (или сжатия), т. е.

где

k – коэффициент упругости или жесткость пружины.

Тогда, для статического равновесия: k·Δl=mg.

При смещении груза из положения равновесия маятника на величину х (рис. 2) баланс сил тяжести и упругости нарушается. Приращение силы упругости определит величину равнодействующей силы , направленной вдоль оси ОХ (рис. 2). Проекция вектора силы на ось ОХ:

.

Таким образом, движение колеблющегося тела будет происходить вдоль оси ОХ под действием силы , и тогда, согласно второму закону Ньютона, уравнение динамики движения груза вдоль оси ОХ будет иметь вид:

где .

Решением этого дифференциального уравнения является гармоническая функция x(t):

, где

х(t) – смещение, то есть отклонение колеблющегося тела от положения равновесия в момент времени t;

– амплитуда гармонического колебания (максимальное отклонение колеблющегося тела от положения равновесия);

₀ – круговая (циклическая) частота колебаний, связанная с периодом колебаний Т и частотой колебаний  следующими соотношениями:

– фаза колебания, определяющая часть полного колебания, прошедшего к моменту времени t;

₀ – начальная фаза колебаний, то есть фаза колебания в начальный момент времени (t=0).

Так как круговая частота колебаний пружинного маятника , то период колебаний пружинного маятника:

Из статического равновесия следует, что

Тогда выражение для периода колебаний пружинного маятника может быть записано в виде:

В проверке этой формулы заключается экспериментальная часть данной лабораторной работы.

.