МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры высшей математики 11.06.2011 г.

Линейное программирование

(для бакалавров 1-го курса

очной формы обучения)

Часть II

Ростов-на-Дону

2011

УДК 517(07)

Линейное программирование (для бакалавров 1-го курса очной формы обучения). Часть II. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 24 с.

Изложены двойственная задача ЛП и ее решение, транспортная задача ЛП и ее решение, особенности решения транспортных задач с неправильным балансом. Приведён образец индивидуального задания, снабжённый подробным решением входящих в него задач.

Предназначены для бакалавров 1-го курса очной формы обучения специальностей ОБД, АС дорожно-транспортного института, а также для бакалавров экономических специальностей.

Электронная версия методических указаний находится в библиотеке, ауд. 224.

УДК 517(07)

Составители: канд. физ.-мат. наук, доц. М. М. Цвиль

канд. физ.-мат. наук, доц.

В. В. Шамраева

ассист. И. В. Цветкова

ассист. В. В. Новиков

Рецензент: канд. физ.-мат.наук, доц. Г.А. Можаев

Редактор Т.М. Климчук

Доп. план 2011 г., поз. 183

Подписано в печать 12.07.11. Формат 60´84/16. Бумага писчая. Ризограф.

Уч.-изд.л. 1,8. Тираж 20 экз. Заказ 385

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов-на-Дону, ул. Социалистическая, 162

Ó Ростовский государственный строительный университет, 2011

6. Теория двойственности

6.1. Построение двойственной задачи

Любой задаче ЛП (исходной) можно поставить в соответствие другую, которая называется двойственной илисопряжённой. Они образуют пару двойственных ( или сопряжённых ) задач ЛП .

Составим двойственную к задаче использования сырья (1.2.1).

Имеется видов сырья в количестве, которые используются для изготовлениявидов продукции. Известно:– расход-го вида сырья на единицу-й продукции;прибыль от реализации единицы-го вида продукции. Составить план выпуска продукции, обеспечивающий максимальную прибыль. Математическая модель данной задачи имеет вид (в матричной форме):

;

;

. (6.1.1)

Здесь ,объём производства-го вида продукции.

Предположим, что второй потребитель хочет перекупить сырьё. Составим двойственную задачу, решение которой позволит определить условия продажи сырья. Введём вектор оценок (цен) видов сырья . Тогда затраты на приобретение сырья в количестверавны. Второму

производителю выгодно минимизировать суммарные затраты на приобретение всех видов сырья, поэтому целевая функция имеет вид

.

Первому производителю невыгодно продавать сырьё, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие -й продукции меньше прибыли, получаемой при реализации этого изделия, т.е.

, .

В матричной форме задача имеет следующий вид:

;

;

. (6.1.2)

Таким образом, связь между исходной и двойственной задачами состоит в том, что коэффициенты целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные членысистемы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.

В теории двойственности используются 4 пары двойственных задач:

Исходная задача	Двойственная задача
Симметричные пары
1.	1.
2.	2.
Несимметричные пары
3.	3.
4.	4. ,

где

С= (c₁,c₂, …,c_n);Y= (y₁,y₂, …,y_m);

; ;.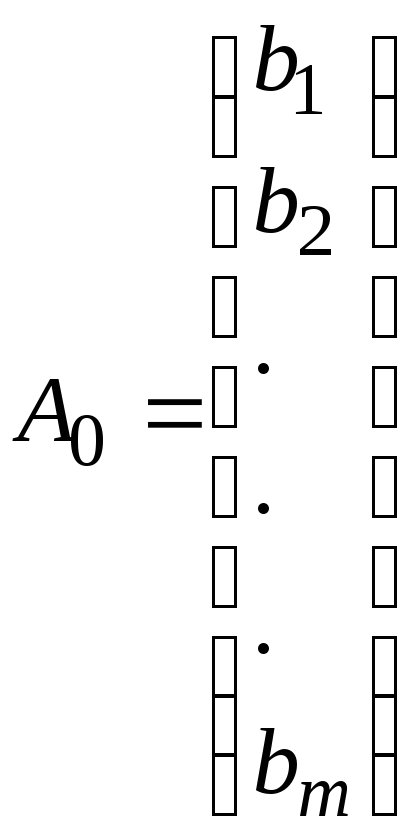