2. Каноническая форма

задачи линейного программирования

2.1. Определение и формы записи

В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической.Она может быть представлена в координатной, векторной или матричной форме записи.

а) каноническая задача ЛП в координатной форме имеет вид:

; (2.1.1)

, .

Данную задачу можно записать, используя знак суммирования:

,

,

, , .

б) каноническая задача ЛП в векторной форме имеет вид: ,

, (2.1.2)

,

где ;;

, ;;.

в) каноническая задача ЛП в матричной форме имеет вид:

,

, ,

где ,,.

2.2. Приведение общей задачи линейного

программирования к канонической форме

При составлении математических моделей экономических задач ограничения в основном формируются в системы неравенств. Поэтому необходимо уметь переходить от них к системам уравнений. Например, рассмотрим линейное неравенство

(2.2.1)

и прибавим к его левой части некоторую величину такую, чтобы неравенство превратилось в равенство.

, (2.2.2)

где .

Неотрицательная переменная называется дополнительной переменной. Следующая теорема даёт основание для возможности такого преобразования.

Теорема 2.2.1.Каждому решениюнеравенства ( 2.2.1) соответствует единственное решениеуравнения (2.2.2) и неравенства, и, наоборот, каждому решению уравнения (2.2.2)ссоответствует решениенеравенства ( 2.2.1).

Доказательство.Пустьрешение неравенства ( 2.2.1). Тогда. Возьмём число. Ясно, что. Подставив в уравнение (2.2.2), получим

.

Первая часть теоремы доказана.

Пусть теперь векторудовлетворяет уравнению (2.2.2) с, т.е.. Отбрасывая в левой части последнего равенства неотрицательную величину, получаем, и т.д.

Таким образом, доказанная теорема фактически устанавливает возможность приведения всякой задачи ЛП к каноническому виду. Для этого достаточно в каждое ограничение, имеющее вид неравенства, ввести свою дополнительную неотрицательную переменную. Причём, в неравенства вида ( 1.2.1) эти переменные войдут со знаком « + », а в неравенствах вида (1.2.2 ) – со знаком « – ». Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому на её значение не влияют.

Замечание. В дальнейшем мы будем излагать симплекс-метод для канонической задачи ЛП при исследовании целевой функции на минимум. В тех задачах, где требуется найти максимум , достаточно рассмотреть функцию, найти её минимальное значение, а затем, меняя знак на противоположный, определить искомое максимальное значение.

3. Графический метод решения задач

линейного программирования

3.1. Общие понятия, примеры

В тех случаях, когда в задаче ЛП лишь две переменные, можно использовать для решения графический метод. Пусть требуется найти максимальное ( минимальное ) значение функции при ограничениях

(3.1.1)

Данный метод основывается на возможности графического изображения области допустимых решений задачи, т.е. удовлетворяющих системе (3.1.1), и нахождения среди них оптимального решения. Область допустимых решений задачи строится как пересечение (общая часть) областей решений каждого из заданных ограничений (3.1.1). Каждое из них определяет полуплоскость с границей ,. Для того, чтобы определить, какая из двух полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.

Пересечение этих полуплоскостей образует некоторую область, называемую многоугольником решений, который является выпуклым множеством. (Допустим, что система ограничений совместна, а многоугольник её решений ограничен.) Для нахождения среди допустимых решений оптимального используются линии уровня и опорные прямые.

Линией уровняназывается прямая, на которой целевая функцияпринимает постоянное значение. Уравнение линии уровня имеет вид

, где . Все линии уровня параллельны между собой . Их нормаль.

Опорной прямойназывается линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений, по отношению к которой эта область находится в одной из полуплоскостей (рис. 1).

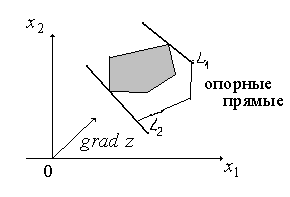
Рис. 1

Значения возрастают в направлении вектора. Поэтому необходимо передвигать линию уровняв направлении этого вектора параллельно самой себе до опорной прямойL₁ в задаче на максимум и в противоположном направлении – в задаче на минимум (до опорной прямойL₂).

Приведём решение примера 1.1. Напомним, что нужно найти максимум функции при ограничениях

Решение. Строим область допустимых решений. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (рис. 2) строим прямую , соответствующую ограничению (1). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1).

Для этого достаточно координаты какой - либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая не проходит через начало координат, подставляемв первое ограничение. Получим строгое неравенство. Следовательно, точкалежит в полуплоскости решений. Аналогично строим прямуюи область решений ограничения (2). Находим общую часть полуплоскостей решений, учитывая ограничения (3). Полученную область допустимых решений выделим на рис.2 тёмным цветом.

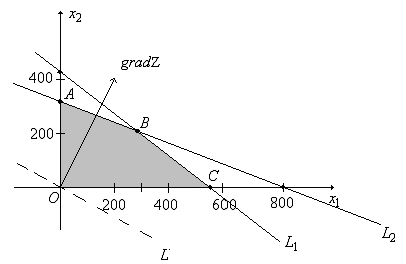
Рис.2

Строим линию уровня и вектор, который указывает направление возрастания функциии перпендикулярен прямой

. Линию уровня перемещаем параллельно самой себе в направлениидо опорной прямой. Получим, что максимума целевая функция достигнет в точкеточке пересечения прямыхи. Решая систему из уравнений этих прямых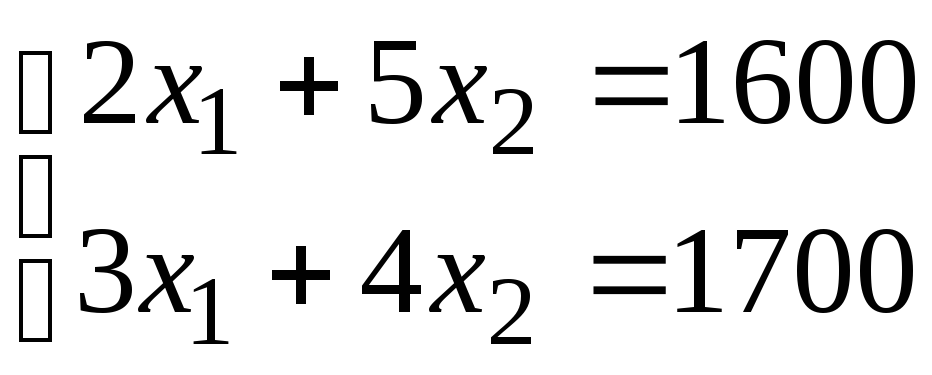, получим координаты точки. Следовательно,, а,оптимальное решение.

Пример 3.1. Найти минимум функции при системе ограничений

Решение. Строим область допустимых решений (см. рис.3), вектор и одну из линий уровня. Перемещаем линию уровня в направлении, противоположном, так как решается задача на отыскание минимума функции. Опорная прямая проходит в этом случае через точку А (рис.3), координаты которой найдём из решения системы

Рис.3

Итак, . Вычисляем.

Замечание. В действительности от вида области допустимых решений и целевой функции задача ЛП может иметь единственное решение, бесконечное множество решений или не иметь ни одного решения.

Пример 3.2. Найти минимум функции при ограничениях

Решение. Строим область допустимых решений, нормаль линий уровня и одну из линий уровня, имеющую общие точки с этой областью. Перемещаем линию уровняв направлении, противоположном направлению нормали, так как решается задача на отыскание минимума функции. Нормаль линий уровняи нормаль граничной прямой, в направлении которой перемещаются линии уровня, параллельны, так как их координаты пропорциональны. Следовательно, опорная прямая совпадает с граничной прямойобласти допустимых решений и проходит через две угловые точки этой областии(рис.4).

Рис.4

Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка . Эти точки,находим, решая соответствующие системы уравнений:

; ;

, ; , ;

; .

Вычисляем .

Ответ: при,.

Пример 3.3. Решить задачу линейного программирования

,

Решение. Строим область допустимых решений, нормаль и одну из линий уровня. В данной задаче необходимо найти максимум целевой функции, поэтому линию уровняперемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых решений не ограничена, линия уровня уходит в бесконечность (рис.5).

Рис. 5

Задача не имеет решения вследствие неограниченности целевой функции.

Ответ: .