НГиЧ / 8.3 МУ. УклонКонусСопр

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании

кафедры начертательной

геометрии и черчения

21 июня 2011г.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ –

УКЛОНЫ, КОНУСНОСТЬ, СОПРЯЖЕНИЯ

Методические указания для всех специальностей

(квалификация выпуска «Бакалавр»)

Ростов-на-Дону

2011

Геометрические построения – уклоны, конусность, сопряжения: методические указания для всех специальностей (квалификация выпуска «Бакалавр»). – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 8с.

Содержатся геометрические построения, необходимые для выполнения задания по инженерной графике.

Электронная версия находится в библиотеке, ауд. 224.

Составитель: ассист. А.В. Федорова

Редактор Н.Е. Гладких

Доп. план 2011 г., поз. 137.

____________________________________________________________________

Подписано в печать 6.07.11. Формат 60х84/16.

Бумага писчая. Ризограф. Уч.-изд.л. 0,3. Тираж 20 экз. Заказ 341.

____________________________________________________________________

Редакционно-издательский центр

Ростовского государственного строительного университета.

344022, Ростов-на-Дону, ул. Социалистическая, 162

Ó Ростовский государственный

строительный университет, 2011

геометрические построения – уклоны, конусность, сопряжения

При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.

В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны, конусность, сопряжения.

Уклоны

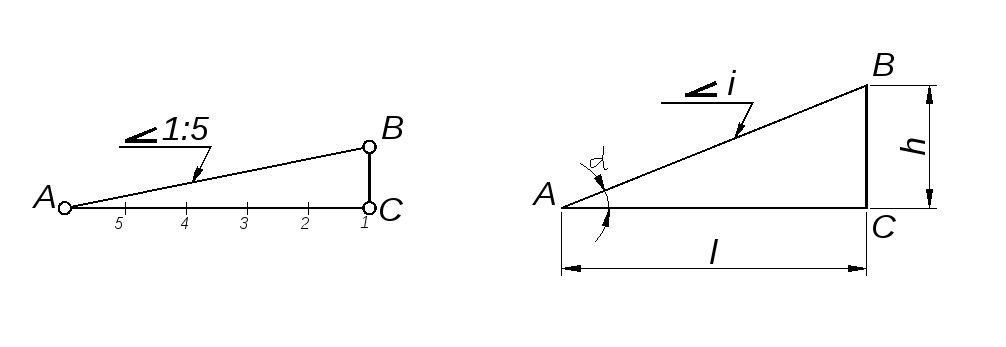
Уклон – наклон одной прямой линии к другой (рис.1). Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.2):

Рис.1 Рис.2

Уклон может быть выражен в процентах (например, уклон в 10% внутренних граней полок швеллера по ГОСТ 8240-89, рис. 3), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ 8168-75*) или в промилях (например, уклон 5‰ арматуры).

Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.

Построение уклонов

1. Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.3).

Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу.

Рис.3

Гипотенуза АС построенного прямоугольного треугольника АВС является искомой прямой с уклоном 1:6.

Построение полок швеллера и двутавра

На рис. 4 и 5 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.

На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2 – для швеллера и (b-d)/4 – для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К, через которую проходит прямая с уклоном 10% для швеллера и 12% - для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.

Рис.4 Рис.5

Конусность

Конусностью называется отношение диаметра окружности основания D прямого конуса к его высоте h (рис.6).

.

Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.7), т.е.

.

Рис.6 Рис.7

Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах. Перед размерным числом, характеризующим конусность, наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.

При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а конусность – отношению диаметра к высоте.

Таким образом, построение конусности i : n относительно данной оси сводится к построению уклонов i : 2n с каждой стороны оси.

Сопряжения

Сопряжением называется плавный переход по кривой от одной линии, прямой или кривой, к другой.

Построение сопряжений основано на свойствах прямых, касательных к окружностям, или на свойствах касающихся между собой окружностей.

Построение касательной к окружности

Рис.8

При построении прямой, касательной к окружности в заданной точке С, проводят прямую перпендикулярно к радиусу ОС. При нахождении центра окружности, касающейся заданной прямой в точке С, проводят через эту точку перпендикуляр к прямой и откладывают на нем величину радиуса заданной окружности (рис.8).

Построение внешней касательной к двум окружностям

Из центра О₁ проводят вспомогательную окружность радиусом R₃ = R₁-R₂ и находят точку К. Построение точки К аналогично построению точки С. Точку О₁ соединяют с точкой К прямой и проводят параллельную ей прямую из точки О₂ до пересечения с окружностью. Точки сопряжения С₁ и С₂ лежат на пересечении прямых О₁К и ранее проведенной линии из центра О₂ с окружностями радиусов R₁ и R₂ (рис. 9).

Рис.9

Сопряжение двух дуг окружностей

При внешнем касании двух окружностей расстояние между центрами О₁ и О₂ равно сумме радиусов R₁ и R₂. Точка касания С лежит на прямой, соединяющей центры окружностей (рис.10).

При внутреннем касании окружностей О₁О₂ = R₁ - R₂. Точка касания С лежит на продолжении прямой О₁О₂ (рис.11).

Рис.10 Рис.11

Сопряжение двух дуг окружностей дугой заданного радиуса

Из центров О₁ и О₂ описываются дуги вспомогательной окружности радиусом R₃ = R + R₁ и R₄ = R + R₂ (при внешнем сопряжении, рис.12) или R₃ = R - R₁ и R₄ = R - R₂ (при внутреннем сопряжении, рис.13). Точка О является центром искомой дуги окружности радиуса R.

Точки сопряжения С₁ и С₂ будут находиться на линии центров О₁О и О₂О (рис.12) или на продолжении линии центров (рис.13).

При нахождении радиуса внешне–внутреннего сопряжения вспомогательные дуги проводятся радиусами R₃ = R - R₁ из центра О₁ и R₄ = R + R₂ из центра О₂ (рис.14).

Сопряжение окружности с прямой по дуге радиуса R

Из центра О₁ проводится дуга радиусом R₂ = R₁ + R и прямая, параллельная заданной, на расстоянии R. Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С₁ лежит на линии центров О₁О, а прямой и дуги сопряжения С – на перпендикуляре, проведенном к заданной прямой из центра О (рис.15).

Рис.12

Рис.13

Рис.14

Рис.15