4. Построить равнобедренный прямоугольный треугольник сde, если задана вершина с, а катет de лежит на горизонтали ав (рис.10).

Рис. 10

Решение. Расстояние от точки С до прямой AB является одним из катетов искомого треугольника. Проекции расстояния от точки С до прямой определяем аналогично первой задаче. Методом прямоугольного треугольника находим натуральную величину отрезка CD (н.в. [СD]). Выявленная натуральная величина равна истинному значению катета прямоугольного треугольника CDE. Для начертания проекций треугольника необходимо натуральную величин отрезка СD (н.в [СD]) отложить на проекции А₁ B₁ отрезка AB от проекции точки D₁. Таким образом, получим проекцию третьей вершины треугольника – точку E₁. По линии связи найдем ее фронтальную проекцию E₂ на проекции отрезка А₂B₂ . Соединив точку E с точкой С ,получим искомый прямоугольный треугольник с вершиной в точке С и катетом, лежащим на горизонтали.

5. Построить равнобедренный прямоугольный треугольник сde, если задана вершина с, а гипотенуза de лежит на горизонтали ав (рис.11).

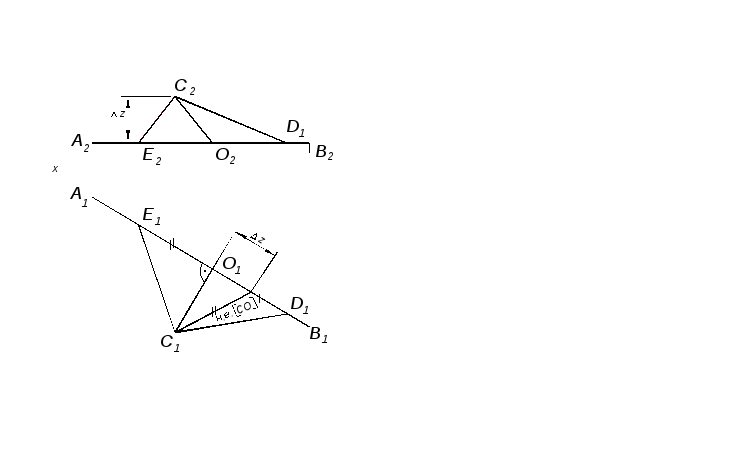
Рис.11

Решение. Расстояние от точки С до прямой AB является высотой искомого треугольника. Проекции расстояния от точки С до прямой определяем аналогично первой задаче. Методом прямоугольного треугольника находим натуральную величину отрезка CО (н.в. [СО]). Выявленная натуральная величина равна истинному значению высоты прямоугольного треугольника CDE. Для начертания проекций треугольника необходимо натуральную величину отрезка СО (н.в [СО]) отложить на проекции А₁ B₁ отрезка AB от проекции точки D₁ по обе стороны. Таким образом, получим проекции второй и третьей вершин треугольника – точки E₁ и D₁. По линиям связи найдем фронтальные проекции точек E₂ и D₂ на проекции отрезка А₂B₂ . Соединив точку C с точками E и D, получим искомый прямоугольный треугольник с вершиной в точке С и гипотенузой, лежащий на горизонтали.

6. Построить ромб CDEF с соотношением диагоналей CE:DF = 1:2, если задана вершина С и известно, что DF расположена на фронтали АВ (рис.12).

Рис.12

Решение. Расстояние от точки С до прямой AB является половиной малой диагонали ромба. Проекции расстояния от точки С до прямой определяем аналогично первой задаче. Для нахождения положения точки Е₂, необходимо продлить проекцию перпендикуляра С₂О₂ и отложить на нем от проекции точки О₂ отрезок, равный О₂С₂. Методом прямоугольного треугольника находим натуральную величину отрезка CЕ (н.в. [СЕ]). Выявленная натуральная величина равна истинному значению малой диагонали ромба CDEF. Для начертания проекций ромба необходимо натуральную величину отрезка СЕ (н.в [СЕ]) отложить на проекции А₂ B₂ отрезка AB от проекции точки О₂ по обе стороны. Таким образом, получим проекции третьей и четвертой вершин ромба – точки F₂.и D₂. По линиям связи найдем горизонтальные проекции точек F₁ и D₁ на проекции А₁B₁ отрезка AB. Соединив последовательно все четыре точки, получим искомый ромб.

Литература

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.: Наука, 1988.

2. Стрижаков А.В., Мартиросов А.Л., Кубарев А.Е. Начертательная геометрия. Ростов н/Д: Феникс, 2004.