2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании

кафедры начертательной

геометрии и черчения

21 июня 2011г.

Методические указания

по начертательной геометрии

«ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ. ТЕОРЕМА О

ПРОЕЦИРОВАНИИ ПРЯМОГО УГЛА»

для студентов всех строительных специальностей

(квалификация выпуска «Бакалавр»)

Ростов-на-Дону, 2011

УДК 744

Методические указания по начертательной геометрии «Взаимное расположение прямых. Теорема о проецировании прямого угла» для студентов всех строительных специальностей (квалификация выпуска «Бакалавр»). Ростов н/Д: Рост. гос. строит. ун-т, 2011. –11с.

Рассмотрены различные взаимные положения прямых в пространстве и приведены правила построения проекций на эпюре. Рассмотрена теорема о проецировании прямого угла, приведены решения основных задач.

Электронная версия находится в библиотеке, ауд. 224.

УДК 744

Составитель: ассист. Д.А.Пашян

Редактор Н.Е. Гладких

Доп. план 2011 г., поз. 132.

Подписано в печать 6.07.11. Формат 60х84/16.

Бумага писчая. Ризограф. Уч.-изд.л. 0,7. Тираж 20 экз. Заказ 336.

Редакционно-издательский центр

Ростовского государственного строительного университета.

344022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2011

Две прямые

Две прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися.

Если две прямые (рис. 1) параллельны (а  b), то их одноименные проекции параллельны (а₁  b₁ и а₂  b₂)*.

Если две прямые пересекаются, то их одноименные проекции тоже пересекаются и точки пересечения этих проекций лежат на одной линии связи*. На рис. 2 прямые с и d пересекаются, так как и горизонтальные проекции с₁, d₁, и фронтальные – с₂, d₂ этих прямых пересекаются, и точки К₁, К₂ их пересечения лежат на одной линии связи.

Если для двух прямых не выполняется ни условие параллельности, ни условие пересечения, то они скрещиваются, например, прямые m и n, е и l (рис. 3).

Рис. 1 Рис. 2

ПРИМЕР 1. Провести произвольную горизонталь h, пересекающую две скрещивающиеся прямые а и b (рис. 4).

Решение. Построение осуществляется в следующем порядке: проводим фронтальную проекцию горизонтали h₂  х в произвольном месте чертежа так, чтобы она пересекла а₂ и b₂. Точки 1₂ = h₂  b₂ и 2₂ = h₂  а₂ –

фронтальные проекции точек пересечения искомой горизонтали с заданными прямыми. Через 1₂ и 2₂ проводим линии связи до пересечения с b₁ и а₁ в точках 1₁ и 2₁. Прямая 1₁2₁, соединяющая эти точки, будет горизонтальной проекцией h₁ искомой горизонтали.

а б

Рис. 3

ПРИМЕР 2. Найти проекции перпендикуляра, опущенного из точки С на горизонталь АВ (рис. 5).

Решение. Горизонтальная проекция С₁D₁ искомого перпендикуляра составит прямой угол с горизонтальной проекцией А₁В₁ заданной прямой. Фронтальную проекцию D₂ точки D найдем на А₂В₂ и соединим ее с С₂. Искомыми проекциями перпендикуляра будут С₁D₁ и C₂D₂.

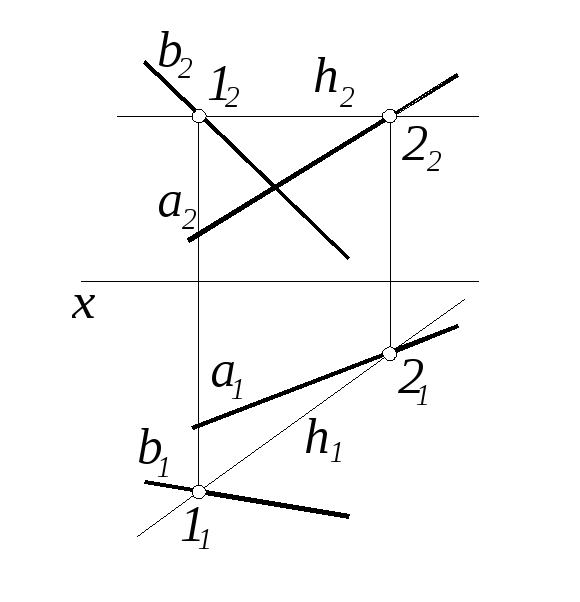
Рис. 4 Рис. 5

ТЕОРЕМА О ПРОЕЦИРОВАНИИ ПРЯМОГО УГЛА

При ортогональном проецировании прямой угол проецируется в прямой тогда, когда одна сторона его параллельна плоскости проекций, а

другая не перпендикулярна этой плоскости На рис. 6 дан прямой угол АВС, лежащий в плоскости, параллельной плоскости . Естественно, что на эту плоскость он проецируется в натуральную величину (А_В_С_ = АВС). Если заданный угол повернуть вокруг одной из его сторон, например, ВС, то сторона АВ переместится в проецирующей плоскости АВВ_А_ в новое положение АВ, но ее проекция останется прежней (А_В_),

Рис. 6 следовательно, проекция угла также

не изменится(А_В_С_ = АВС).

ПРИМЕРЫ: