Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный социальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

СФ / Надежность строительных конструкций

.pdf

Скачиваний:

122

Добавлен:

12.06.2015

Размер:

637.41 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

КАФЕДРА ТЕОРЕТИЧЕСКОЙ И ПРИКЛАДНОЙ МЕХАНИКИ

Мущанов В.Ф., Касимов В.Р., Руднева И.Н.

КОНСПЕКТ ЛЕКЦИЙ

ОСНОВНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ПО МЕТОДУ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ

Макеевка, ДонНАСА 2009

УДК 624.04

Конспект лекций «Основные положения расчет строительных конструкций по методу предельных состояний (для студентов строительных специальностей) / Составители: Мущанов В.Ф., Касимов В.Р., Руднева И.Н. – Макеевка, ДонНАСА, 2009. – 36 с.

Конспект лекций «Основные положения расчет строительных конструкций по методу предельных состояний предназначен для студентов строительных специальностей. В конспекте лекций рассматриваются вопросы вероятностного расчета строительных конструкций, частные коэффициенты надежности метода предельных состояний, нормирование атмосферных и технологических (крановых) нагрузок, сочетание нагрузок.

Составители:	проф. В. Ф. Мущанов
	доц. Касимов В.Р.
	ас. Руднева И.Н.
Рецензенты:	к-т техн. наук, доц. Жук Н.Р.
	к-т техн. наук, доц. Жук Н.Р.
	к-т техн. наук, доц. Денисов Е.В.
Ответственный за выпуск	проф. В. Ф. Мущанов

ЛЕКЦИЯ № 1. ОСНОВЫ ВЕРОЯТНОСТНОГО РАСЧЕТА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

Проектирование конструкций является процессом принятия решений, при котором необходимо учитывать различные неопределенности в виде возможных отклонений параметров нагрузки, геометрии, прочности материала от заданных значений для достижения приемлемой вероятности «отказа» конструкции.

Основные определения:

Надежность – способность объекта выполнять свои функции в течение установленного срока службы.

Отказ – реализация состояния объекта, при котором он не может выполнять свои функции.

Основные сведения из теории вероятности и математической статистики

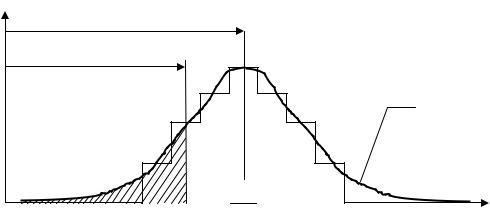
При конечном числе интервалов, на которые разбивается диапазон измерения случайной величины Х, результаты измерений (в простейшем случае) могут быть представлены в виде гистограммы (см. Рис. 1).

ni/N	x
(px)
	px(x)

						px(x)
xi-3	xi-2	xi-1	xi	xi+1	xi+2	xi+3

Рис.1.

xi – интервал случайной величины; ni – число попаданий случайной величины в интервал xi; N – число испытаний;

При N → ∞ и i → ∞ получаем непрерывную функцию px(x) – функцию

плотности распределения (или просто плотность распределения) случайной величины Х,

Основные свойства px(x):

1. Суммарная площадь под кривой плотности распределения равна 1, т.е.:

∞	(x)dx =1,
∫ px	(x)dx =1,	(а)
−∞

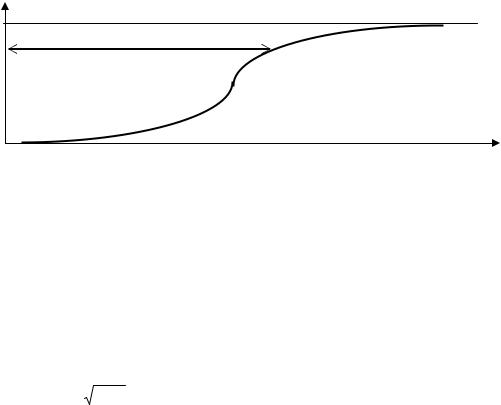
а вероятность (Рх(х))того, что случайная величина Х примет значение меньше х будет равна участку площади, расположенной под кривой px(x) левее х, или

		x
Px (x)= ∫ px (x)dx -			функция распределения				вероятности. Из этого следует 2-е
		−∞
свойство:
	2. Плотность		распределения есть				первая производная от функции
вероятности распределения
				px (x)=	dPx (x)			(б)
	P(x)			px (x)=	dx			(б)
	P(x)				dx

	1
			x




						Px(x)

Рис. 2. Функция распределения вероятности

Плотность распределения px(x), как и функция распределения, характеризует в полном объеме случайную величину Х, основными характеристиками которой являются:

∞

1) математическое ожидание x = ∫ xpx (x)dx - абсцисса центра тяжести площади

−∞

под кривой распределения;

	∞	(x − x )2 px (x)dx - дисперсия случайной величины Х;
2)	D(x)= x) = ∫	(x − x )2 px (x)dx - дисперсия случайной величины Х;	(в)
	−∞
3)	S(x)= x€ = D(x) - стандарт случайной величины Х.

Величины 2) и 3) характеризуют рассеяние (изменчивость) случайной величины

Х.

Основы расчета надежности конструкций

Если представить расчетные параметры, влияющие на работу конструкции, в виде случайных независимых величин, то условие обеспечения несущей способности конструкции может трактоваться, как выполнение предельного неравенства:

,..., x

, x

,..., x

)> 0;

(1)

g(x , x

)= R(x , x

)−Q(x

n ~

m+1

m+2

или

−Q

> 0 ,

где

“~”

–

символ

случайной

величины;

- усилия

(или напряжения) в

конструкции,

выраженные

через внешнюю нагрузку;

несущая способность

конструкции,

выраженная

единицах

представления

- функция резерва

прочности.

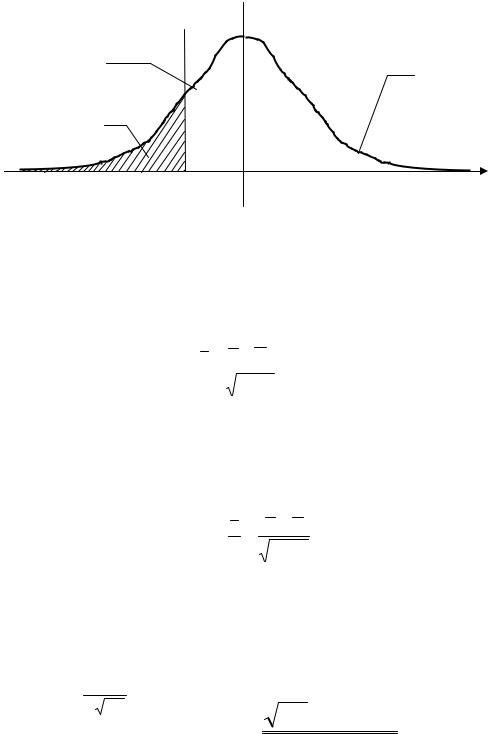
Вероятность выполнения неравенства (1) есть вероятность неразрушения. Вероятность разрушения конструкции (или ее отказа, превышения границы области допустимых состояний) определится, как

	0
Pf	= ∫ pg (g)dg	(2)
	−∞

где pg(g) – плотность распределения функции резерва прочности.

p(g)

pg(g)

Pf = P(g<0)

0 β(g)

Рис.3. К определению надежности конструкции

При любых законах распределения взаимно-независимых случайных величин

~ ~ справедливы соотношения:

R и Q

			g = R −Q;					(3)
			g€ =	R) −Q),				(3)
–,	, ∩ - математическое ожидание, дисперсия, стандарт величины.
Число стандартов g€, укладывающееся в диапазоне от g = 0 до g = g называется
характеристикой безопасности β
			β =	g	=	R −Q		(4)
			β =	g€	=	)	)	(4)
				g€		R +Q
Для	простоты	иллюстрации взаимосвязи					между Pf и β предположим,	что
случайные величины		~	~
случайные величины		R и Q подчиняются нормальному закону распределения. В этом

случае вероятность отказа будет вычисляться, как (см. рис. 2)

−

∞

= P(g < 0)=

−

€

∫ e

dg =

−

g€

2π −∞

1	β	g 2
	∫ e−		dg =	1	−Φ(β)	(5)
		2
				2
2π
	0

Φ(β )

где Ф(β) – интеграл вероятности Гаусса.

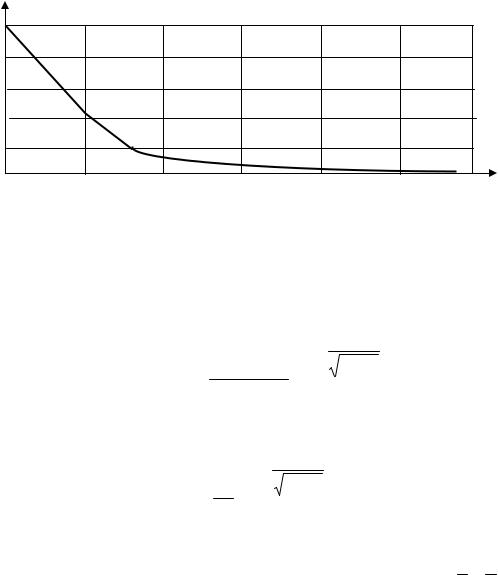
Pf 0.5

0.4

0.3

0.2

0.1

Рис. 3. К зависимости между Pf и β

В общем случае рассматриваемый подход позволяет исследовать вероятностную природу коэффициентов надежности метода предельных состояний:

-для коэффициента надежности по нагрузке γf:

					€
			1+		Qβv	Q)
		Qp	1+		)	Q)
γ f =		Qp			R +Q		(6.a)
		(1+ µQ vQ )=
				1+ µQ vQ
	Q			1+ µQ vQ

-для коэффициента надежности по материалу γm

€

Rβv

)

R +Q

(6.б)

€

γ m

+ µR vR

где

vQ =

vR =

- коэффициенты вариации; µQ и µR

- число стандартов, на

которые сдвинуты нормативные значения Rn и Qn по отношению к R и Q .

Всвязи с этим можно считать, что:

-основные положения метода предельных состояний имеют вероятностную основу;

-отсутствие прямого вероятностного расчета в рамках методики предельных состояний приводит к следующим негативным последствиям:

надежность сооружений одного и того же назначения, запроектированных по одним и тем же нормам, но выполненных из различных материалов, оказывается различной;

существующие нормы расчета и проектирования не позволяют оценивать надежность проектируемых конструкций, а тем более, проектировать конструкции с заданным уровнем надежности.

Исключить указанные недостатки позволяет прямой вероятностный расчет конструкций.

ЛЕКЦИЯ №2. МЕТОДЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТИ ОТКАЗА

Условием отказа будет выполнение неравенства:
~	~	< 0	(7)
R	−Q

Вероятностью отказа будет вероятность реализации неравенства (7)

∞

Pf = ∫ R(x)pQ (x)dx (8)

где R(x) – функции распределения вероятностей случайной величины R; pQ(x) – плотность распределения вероятностей Q.

Для вычисления вероятности отказа в виде интеграла (8), используются следующие методы:

1) метод 2-х моментов – используется, если величины			~	~	распределены по
1) метод 2-х моментов – используется, если величины			R и Q		распределены по
нормальному закону. Тогда	1 − Φ(β)=1 − P
P =	1 − Φ(β)=1 − P				(9)
f	2	S
	2

Преимущество метода в его простоте, недостаток – в ограниченности применения нормального закона распределения.

2) метод статистической линеаризации – основан на разложении функции надежности g~ в ряд Тейлора. Применяется, как правило, при определении числовых

характеристик нелинейной функции g нескольких случайных аргументов x1, x2, … , xn.

Пусть g = f(x1, x2, … , xn)

Разложим функцию g в ряд Тейлора в окрестности точки А:

∂g

g =

f (a1 , a2 ,..., an )+ (x1

− a1 )

+ (x2

− a2 )

+... +

(xn − an )

+W ,

(10)

∂x

∂g

где

- значения

частных

производных,

которые

берутся

при

∂xi

(i =1,2,..., n); W – нелинейные члены ряда.

xi = ai

В практических расчетах членами W как правило пренебрегают. Тогда:

математическое ожидание функции

надежности

(g )

определяется, как

функция g, вычисленная от математических ожиданий случайных

аргументов x1, x2 ,..., xn , т.е.

g(x1 , x2 ,..., xn )≈ f (x1 , x2 ,..., xn )

(11.a)

-дисперсия функции g определится, как

)	n	∂g 2	)
g	≈ ∑		xi	(11.б)

	i=1	∂xi

3) метод «горячих» точек, разработанный в бывшем СССР Б.И. Снарскисом (он же в зарубежной литературе метод первого приближения, сформулированный Хазофером и Линдом). Метод используется в случае, если исходные величины

распределены не по нормальному закону, и основан на приведении исходных распределений к нормальному. Аппроксимации производятся в «горячей точке» (точке подгонки).

Преимущество метода заключается в универсальности и простоте алгоритма, недостатки – в том, что функция g , определяющая область отказа, должна быть

всюду дифференцируемой и гладкой.

4) метод статистических испытаний, основанный на достаточно большом числе (5000 … 10000) статистических испытаний по схеме Бернулли, т.е. при каждом

		~	~
испытании генерируются значения случайных величин R и Q . Для i-х значений xi
выполняется детерминированный расчет значений Q и R и проверяется условие Q >
R. Если условие выполняется, то эта реализация засчитывается в качестве отказа.
Частота появления отказа (ν) рассматривается, как оценка его вероятности Pf:
ν =	k	≈ P	(12)

	m	f

где k – число отказов; m – число испытаний.
Метод крайне прост и универсален, но требует оценки близости ν к Pf. Тогда
Pf ≤ηskν,			(13)
где ηsk - доверительный коэффициент, определяемый,			как правило, по таблицам

в зависимости от уровня доверительной вероятности Ps и числа отказов k. Например:

для Ps = 0.95 и k = 20 при m = 5000

→ν = 500020 = 0.004; η020.95 =1.453; Pf =1.453 0.004 = 0.005812;

для Ps = 0.99 и k = 20 при m = 5000

→ν = 500020 = 0.004; η020.99 =1.655; Pf =1.655 0.004 = 0.00622.

5) метод Монте-Карло – является модифицированным методом статистического моделирования. Так как интеграл (8) есть не что иное, как математическое ожидание функции отказа Fk, то

			1	m
Pf =		(Q)≈		∑Fk (Qi )	(14)
	F

			m i=1

т.е. при каждом испытании:

а) по заданной плотности вероятностей величины Q моделируется ее реализация

Qi;

б) по значению аргумента Qi определяется значение R; в) проверяется условие Ri −Qi = Fki ;

г) по выше приведенной формуле (14) определяется Pf.

Как и в предыдущем случае, необходимой операцией является оценка близости ν к Pf. При реализации метода Монте-Карло наиболее приемлемым подходом является формирование ряда выборок Pf (до i = 20) и формирования на их основе значений оценки вероятности Pfi . Для определения доверительного интервала ∆Pf

используем критерий Стьюдента

	2		2
	2		2
∆Pf = ±t p	∑Pfi	− MPfi		(15)
	i=1
	M (M −1)
	M (M −1)

М – число выборок; tp – значения коэффициента для различных уровней доверительной вероятности.

При большой ширине доверительного интервала следует увеличить объем выборок или их число.

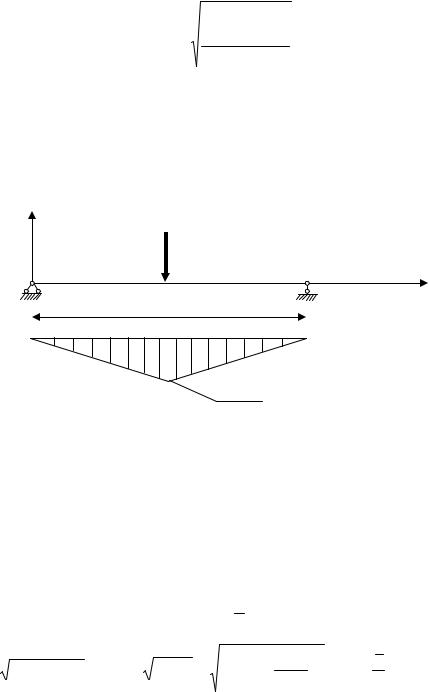
Пример расчета вероятности отказа методом 2-х моментов

Расчет на прочность балки в условиях плоского поперечного изгиба

M =

;

Wx =

;

при

R =σT

Q =σ =

6Pl

3Pl

4bh2

2bh2

Mmax

Рис. 5

Примем

величины

распределенными

по

нормальному закону

P и σ~T

характеристиками

€

Остальные

параметры

считаем

неизменными

σT и σ€T , P и P .

(детерминированными).

Если величины R и Q распределены по нормальному закону, тои

результирующая величина g подчиняется нормальному закону распределения:

Так как g(x + y)= g(x)+ g(y), то g =

−

T −

;

=σ

2bh2

a g€(x + y)=

)

) 3l

; β =

g(x)+ g(y), то g€ =

R +Q

σT

+ P

g€

2bh2

Вероятность безотказной работы: P =

+ Φ(β);

Вероятность отказа:

−Φ(β)=1− P .

Тогда при

€

σ€T

= 2.6 kH , σT = 240 MΠa = 240000kH / м

= 24 MΠa =

24000 kH / м

P = 26 kH , P

детерминированных величинах l = 2 м, b = 0.05 м, h = 0.1 м

g =σT − P		3l	= 240000 − 26				3 2		0.12	=	84000 kH / м2 ;
		2bh2					2 0.05		0.12
)	+	) 3l		2	24000	2	+ 2.6	2		3 2					2			2	,
g€ = σT	+	P		=	24000		+ 2.6		2 0.05 0.12						= 28624.5 kH / м				,
		2bh2							2 0.05 0.12
β = g =	84000		= 2.935
g€	28624.5
Вероятность безотказной работы:									P =			1	+ Φ(β)=			1	+ Φ(2.935)= 0.9984,
Вероятность безотказной работы:									P =				+ Φ(β)=				+ Φ(2.935)= 0.9984,
									s		2				2
Вероятность отказа:											2				2
Вероятность отказа:									Pf =1− Ps					=1−0.9984 = 0.0016 или 0.16%.

ЛЕКЦИЯ №3. МЕТОД ПРЕДЕЛЬНЫХ СОСТОЯНИЙ

Предельное состояние есть состояние, при переходе за которое сооружение перестает соответствовать поставленным требованиям. В настоящее время предельные состояния по степени ограничений и эксплуатации и возможных последствий отказа разделяются на 2 группы:

•к 1-й группе относятся предельные состояния, при выходе за которые возникает полная потеря пригодности к эксплуатации (общая потеря устойчивости, потеря устойчивости положения, разрушение любого характера, переход в изменяемую систему, качественное изменение конфигурации вследствие чрезмерных деформаций ползучести или пластичности, сдвигов в соединениях),

•ко 2-й группе относятся предельные состояния, при выходе за которые затрудняется нормальная эксплуатация (недопустимые деформации и перемещения, недопустимые уровни колебаний, недопустимые образования

или раскрытия трещин).

Для количественных оценок предполагается математическая модель , в которой возможно описание предельного состояния с помощью уравнений или алгоритма в зависимости от величин, допускающих их прямое измерение или наблюдение. Эти величины в теории надежности несущих конструкций называются базисными переменными Xi. Большей частью базисные переменные (нагрузки, свойства материала и грунтов, геометрические размеры) являются случайными числами, иногда случайными процессами, для которых может быть собрана статистическая информация. Совокупность определяющих надежность сооружения базисных переменных представляется случайным вектором

	X	1
	.	1
	.
X =	.		(16)
	.
	.

	X m

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке СФ

#
12.06.2015283.55 Кб69Внутренняя среда жилища.docx
#
12.06.20151.99 Mб91Компьютерные расчетные программы.pdf
#
12.06.2015637.41 Кб122Надежность строительных конструкций.pdf
#
12.06.20152.13 Mб148Расчеты жб конструкций.docx
#
12.06.2015792.4 Кб68Расчеты прочности зданий и сооружений.pdf
#
12.06.2015183.1 Кб138Строймех.pdf