Приложение
Формирование матрицы жесткости плоского треугольного конечного элемента в локальной системе осей координат
Для расчета конструкций, испытывающих плоское напряженное состояние,
плоский треугольный конечный элемент явяляется одним из наиболее удобных типов конечных элементов, т.к. позволяет наиболее просто и удобно получить на конструкции сетку узлов требуемой густоты.
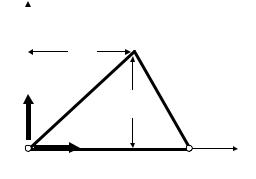
Рассмотрим процесс формирования матрицы жесткости плоского треугольного 3-х узлового конечного элемента с узлами i, j, m, обозначенными в направлении обхода против часовой стрелки.
y1
m xm 
vi
ym
i |
ui |
j |
x1 |
|
К построению матрицы жесткости треугольного КЭ
Смещения в узле имют 2 компонента - ui и vi. Тогда вектор узловых смещений
элемента может быть представлен как
|
|
ì ui |
ü |
|
|
|
|
ï |
|
ï |
|
|
|
ï vi |
ï |
|
|
{z} |
e |
ïu |
j |
ï |
(1) |
|
= í |
ý |
|||
|
|
ïv j |
ï |
|
|
|
|
ïum |
ï |
|
|
|
|
ï |
|
ï |
|
|
|
îvm |
þ |
|
|
Самое простое представление смещения u и v точек с координатами x и y внутри
элемента через смещения узловых точек может быть получено на основе использования 2-х линейных многочленов:
u = α 1 |
+α 2 x +α 3 y, |
(2) |
|||
v = α 4 |
+α |
5x +α |
6 y |
||
|
|||||
Постоянные α1 − α6 можно получить, решая две системы из 3-х уравнений, введя координаты узлов и приравняв их смещения соответствующим узловым смещениям:
ui = α 1 + α 2 xi + α 3 yi ; |
vi = α 4 + α 5xi +α 6 yi ; |
|
uj = α 1 + α 2 x j + α 3 y j ; |
v j = α 4 + α 5x j +α 6 y j ; |
(3) |
um = α 1 + α 2 xm + α 3 ym ; |
vm = α 4 + α 5 xm + α 6 ym . |
|
Подставив решения систем (3) в выражения (2) окончательно получим выражения для u и v
u = 21 [(ai + bi x + ci y)ui + (a j + bj x + cj y)uj + (am + bm x + cm y)um ], (4) v = 21 [(ai + bi x + ci y)vi + (a j + bj x + cj y)v j + (am + bm x + cm y)vm ],
где - площадь треугольника,
ai = x j ym − xm y j ; bi = y j − ym ; ci = xm − x j .
Коэффициенты aj, bj, cj, am, bm, cm можно получить циклической перестановкой индексов в последовательности i, j, m.
Относительная деформация в любой точке элемента определяется с помощью трех компонентов, вносящих вклад во внутреннюю работу, которая с помощью уравнений (4)
может быть записана как
|
|
ì |
∂u |
ü |
|
ì |
ε x ü |
ï |
∂x |
ï |
|
ï |
ï |
|
|||
ï |
ï |
ï |
∂v |
ï |
= |
{ε} = í |
ε y ý |
= í |
∂y |
ý |
|
ï |
ï |
ï |
ï |
|
|
îγ xy þ |
ï |
∂u + |
∂v ï |
|
|
|
|
ï |
∂y |
ï |
|
|
|
î |
∂x þ |
|
|
1 éêbi
2 ê0
êëci
0 |
b |
j |
0 |
b |
0 ù |
|
|
|
|
|
|
m |
cm úú{z}e = [B]{z}e |
(5) |
|
ci |
0 |
cj |
0 |
||||
b |
c |
j |
b |
j |
c |
b ú |
|
i |
|
|
m |
m û |
|
||
Учитывая, что для треугольного элемента постоянной толщины общее выражение для матрицы жесткости может быть упрощено, т.е.
[k]e = ò[B]T [D][B]dV = [B]T [D][B]t |
(6) |
V |
|
и учитывая, что матрица упругости ( закона Гука) для случая плоского напряженного
состояния имеет вид
|
|
|
é |
1 |
μ |
0 |
ù |
|
|
[D] = |
|
E |
ê |
ú |
|
||||
|
ê |
μ |
1 |
0 |
ú |
(7) |
|||
|
- μ |
2 |
ê |
ú |
|||||
1 |
ê |
0 |
0 |
1- μ |
ú |
|
|||
|
|
|
ê |
2 |
ú |
|
|||
|
|
|
ë |
|
|
û |
|
||
окончательно выражение для матрицы жесткости плоского треугольного элемента имеет вид:
|
|
|
|
|
|
ék11 |
k12 |
||
|
|
|
|
|
ê |
|
k22 |
||
|
|
|
|
|
|
êk21 |
|||
k |
e |
= |
Et |
|
êk31 |
k32 |
|||
|
( |
|
) ê |
|
|
|
|||
[ ] |
|
|
- μ 2 |
|
k42 |
||||
|
|
4 1 |
|
êk41 |
|||||
|
|
|
|
|
|
êk |
51 |
k |
52 |
|
|
|
|
|
ê |
k |
|||
|
|
|
|
|
|
êk |
61 |
62 |
|
|
|
|
|
|
ë |
|
|||
k13 |
k14 |
k15 |
k23 |
k24 |
k25 |
k33 |
k34 |
k35 |
k43 |
k44 |
k45 |
k53 |
k54 |
k55 |
k63 |
k64 |
k65 |
k16 ù k26 úú
k36 úú (8)
k46 ú k56 úú k66 úû
где |
|
1- μ |
|
|
|
|
1- μ ö |
|
|
|
1- μ |
|
|
|
= bi2 + ci2 |
|
|
æ |
μ + |
|
|
|
|
||||
k11 |
|
; k12 |
= k21 |
= bi ci ç |
|
÷ |
; k13 |
= k31 = bi bj |
+ ci c j |
|
; |
||
2 |
|
2 |
|||||||||||
|
|
|
|
è |
|
2 ø |
|
|
|
|
|||
k |
|
= k |
|
= b c |
|
μ + b |
|
c |
|
1- μ |
|
; k |
|
|
|
|
= k |
|
|
= b b |
|
|
|
|
+ c c |
|
|
1- μ |
; k |
|
|
|
= k |
|
|
= b |
c |
|
μ + c b |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
14 |
|
41 |
i |
|
j |
|
|
|
|
j i |
|
|
|
|
|
|
15 |
|
|
|
|
51 |
|
|
|
|
i |
m |
|
|
i |
m |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
61 |
|
|
i |
|
|
|
m |
|
|
|
i |
m |
||||||||||||||||||||
k |
|
= c |
2 |
+b2 |
1- μ |
|
; k |
|
|
|
= k |
|
|
= b |
|
c |
|
μ +b c |
|
|
1- μ |
; k |
|
|
= k |
|
|
= c c |
|
|
+ b b |
|
|
1- μ |
; |
|
|
|||||||||||||||||||||||||||||||||||||||||||
22 |
i |
|
23 |
32 |
j |
j |
|
|
|
|
24 |
42 |
j |
|
j |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
k |
|
= k |
|
= b |
|
|
c |
|
μ + b c |
|
|
1- μ |
; k |
|
|
|
= k |
|
= c c |
|
|
+b b |
|
|
1- μ |
; k |
|
|
= b |
2 |
+ c2 |
1- μ |
; |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
25 |
|
52 |
|
m |
i |
|
|
|
i |
m |
|
|
|
|
26 |
|
|
|
|
62 |
|
|
|
|
|
i |
m |
|
|
i |
|
m |
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
j |
|
|
j |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
1- μ ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
k34 |
= k43 |
= bj c j ç μ + |
|
|
|
|
|
|
|
÷; k35 = k53 |
|
= bj bm + c j cm |
|
|
|
|
|
|
|
; k36 = k63 |
= bj cm μ +bmc j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k |
|
= c2 |
+ b2 |
1- μ |
|
; k |
|
|
|
= k |
|
|
= b |
|
|
c |
|
μ +b |
|
|
c |
|
|
|
1- μ |
; k |
|
|
|
= k |
|
|
= c |
|
c |
|
|
+b |
|
b |
|
|
1- μ |
; |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
44 |
|
j |
j 2 |
|
|
|
|
|
45 |
|
|
54 |
|
|
|
m |
|
j |
|
|
|
|
j |
|
|
m |
|
|
|
|
2 |
|
|
|
|
|
|
46 |
|
|
|
|
|
|
64 |
|
|
|
|
|
j |
|
m |
|
j |
|
|
|
|
||||||||||||||||||||
|
|
= bm2 + cm2 |
|
1- μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
μ + |
1- μ |
ö |
|
|
|
|
|
|
= cm2 +bm2 |
1- μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
k55 |
|
|
|
|
|
|
|
; k |
56 = k65 |
= bmcm ç |
|
|
|
|
|
|
|
|
|
|
÷; k |
66 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1-2μ ;
1-2μ ;
Использование полученной матрицы жесткости в дальнейших конечно-
элементных операциях ничем не отличается от использования матрицы жесткости стержневого конечного элемента. Естественно, результатом расчета в этом случае будут усилия соответствующие компонентам перемещений, указанным на Рис. , т.е. N x,1 ,N y,1 ,N x,2 ,N y ,2 ,Nx ,3 ,N y,3 , которые могут быть преобразованы к напряжениям в центре
тяжести конечного элемента (σ x ,σ y ,τ xy ).