
Теория_Вероятностей_КР7
.pdf
27
Тогда по формуле полной вероятности
P( A) = P(Н1)P( A / Н1) + P(Н2 )P( A / Н2 ) + P(Н3 )P( A / Н3 ) + P(Н4 )P( A / Н4 ) = 0,6044 . ►
2.7. Формула Байеса
Если известно, что в результате опыта событие A произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие A происходит с большей вероятностью, и уменьшаются вероятности остальных. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса, которая является следствием теоремы умножения вероятностей и формулы полной вероятности:
P(Hi / A) = |
P(Hi ) P( A / Hi ) |
, |
(2.14) |
|
P(A) |
||||
|
|
|
n
где P( A) = ∑ P(Hi )P( A / Hi ) — формула полной вероятности.
i=1
Заметим, что вероятности гипотез Hi , принятых до опыта называют апри-
орными, а переоцененные по результатам уже проведенного опыта — апостери-
орными вероятностями.
Пример 2.32. 30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного спе-
циалистом высокой квалификации 0,9, надежность прибора, собранного специа-
листом средней квалификации 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.
Решение. Обозначим следующие гипотезы:
Н1 – «прибор собран специалистом высокой квалификации»; Н2 – «прибор собран специалистом средней квалификации».
Вероятности гипотез: P(Н1) = 0,3, P(Н2 ) = 0,7 ( P(H1) + P(H2 ) = 1).
Событие А – «безотказная работа прибора». По условию задачи необходимо найти вероятность гипотезы H1 при условии, что событие А произошло –
P(H1 / A) .
Условные вероятности события А: P(A / Н1) = 0,9 , P( A / Н2 ) = 0,8 .
Вероятность события А: P(A) = 0,3 0,9 + 0,7 0,8 = 0,83.
Воспользуемся формулой Байеса:
P(Н1 / A) = P(Н1)P(A / Н1) = 0,3 0,9 = 0,325. P( A) 0,83
Можно заметить, что вероятность гипотезы H1 увеличилась. ►
28
Пример 2.33. Два руководителя планируют создать совместное предприятие, если в течение года каждому из них удастся сформировать свою долю начального ка-
питала. Вероятности этого равны соответственно p1 и p2 . По истечение года вы-
яснилось, что совместное предприятие не может быть создано. Какова вероят-
ность того, что оба участника не сумели накопить свою долю начального капита-
ла?
Решение. Обозначим следующие гипотезы: Н1 – «оба участника накопили капитал»;
Н2 – «первый накопил, а второй — нет»;
Н3 – «второй накопил, а первый — нет»;
Н4 – «оба участника не накопили капитала». |
|
|
|
||
Найдем вероятности гипотез: |
P(H1) = p1 p2 , |
P(H2 ) = p1(1− p2 ) , |
|||
P(H3 ) = (1− p1) p2 , |
P(H4 ) = (1− p1)(1− p2 ) . |
Нетрудно |
проверить, |
что |
|
P(H1) + P(H2 ) + P(H3 ) + P(H4 ) = 1.
Наблюдалось событие А — «совместное предприятие не может быть создано», которое могло произойти со следующими условными вероятностями:
Р(А/Н1) = 0, P(A/H2) = Р(А/Н3) = Р(А/Н4) = 1.
Следовательно, по формуле полной вероятности
P(A) = P(H2 ) + P(H3 ) + P(H4 ) = 1− P(H1) = 1− p1 p2 .
Тогда по формуле Байеса P(H4 / A) = |
P(H4 ) |
= |
(1− p1)(1− p2 ) |
. ► |
P(A) |
|
|||
|
|
1− p1 p2 |
||
Пример 2.34. Есть два золотоносных района, поделенных на четыре участка каж-
дый, причем по прогнозам известно, что в первом районе три участка из четырех,
а во втором районе два участка из четырех являются золотоносными. Наугад выбран район и куплен один участок, который оказался золотоносным. Какова веро-
ятность вторичной удачной покупки.
Решение. Обозначим следующие гипотезы: Н1 – «выбран первый район»;
Н2 – «выбран второй район».
Вероятности гипотез: P(H1) = P(H2 ) = 12 .
Событие А — «первый раз куплен золотоносный участок». Условные вероятности события А: P( A/ H1) = 3 4 , P(A / H2 ) = 1
4 , P(A / H2 ) = 1 2 .
2 .
По формуле полной вероятности P(A) = 12 34 + 12 12 = 85 .
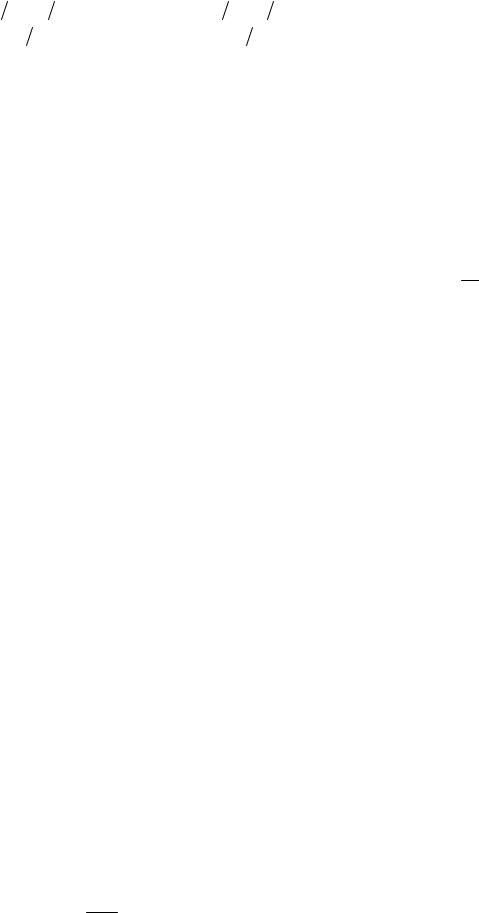
|
|
|
|
|
|
29 |
|
|
|
|
|
Апостериорные |
|
|
вероятности |
исходных |
гипотез |
равны |
|||
P(H1 |
/ A) = |
(1 2) (3 4) |
= |
3 |
, P(H2 / A) = |
(1 2) (1 2) = |
2 . |
|
|
|
|
|
(5 8) |
|
5 |
|
(5 8) |
|
5 |
|
|
Для вторичного эксперимента с покупкой участка можно ввести снова две гипотезы, связанные с его предысторией: H1' — «выбран первый район, на кото-
ром впервые был куплен золотоносный участок», H2' — «выбран второй район,
на котором был куплен золотоносный участок». Тогда P(H1' ) = 3 5, P(H2' ) = 2
5, P(H2' ) = 2 5 .
5 .
Пусть B — вторичная покупка золотоносного участка. Очевидно, что
P(B / H1' ) = 2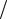 3 , P(B / H2' ) = 1
3 , P(B / H2' ) = 1 3 .
3 .
Тогда вероятность вторичной удачной покупки по формуле полной вероят-
ности равна P(B / A) = P(H1' )P(B / H1' ) + P(H2' )P(B / H2' ) = 53 23 + 52 13 = 158 . ►
3. Повторные независимые испытания
3.1. Формула Бернулли
Рассмотрим случай, когда требуется определить вероятность того, что событие А произойдет заданное количество раз в серии из n опытов. Будем считать при этом, что вероятность A в каждом опыте одинакова и результат каждого опыта не зависит от результатов остальных. Такая постановка задачи называется
схемой независимых испытаний или схемой Бернулли. При выполнении указанных условий вероятность того, что при проведении n независимых испытаний событие A будет наблюдаться ровно k раз (неважно, в каких именно опытах), опреде-
ляется по формуле Бернулли:
Pn (k) = Cnk pk qn−k , |
(3.1) |
где p — вероятность появления A в каждом испытании, а q = 1− p |
— вероят- |
ность того, что в данном опыте событие A не произошло. |
|
Пример 3.1. Победу в волейбольном матче одерживает команда, выигравшая 3 партии. Найти вероятность того, что матч между командами, для которых вероят-
ность выигрыша каждой партии равна соответственно 0,8 и 0,2, будет состоять из
5 партий.
Решение. Для того, чтобы потребовалось играть пятую партию, нужно, чтобы
после четырех партий счет в матче был 2 : 2 . Следовательно, каждая из команд должна выиграть любые две партии из четырех. Если p = 0,8 есть вероятность
выигрыша в каждой партии для первой команды, а q = 0,2 — вероятность ее проигрыша, то, применяя формулу Бернулли (3.1), найдем, что
P4 (2) = С42 0,82 0,22 = 2!4!2! 0,64 0,04 = 0,1536. ►
30
Вероятность того, что в n опытах схемы Бернулли событие А появится от k1 до k2 раз ( 0 ≤ k1 ≤ k2 ≤ n ) обозначим Pn (k1 ≤ k ≤ k2 ) , тогда
k2 |
k2 |
|
Pn (k1 ≤ k ≤ k2 ) = ∑ Pn (k) = |
∑Cnk pk qn−k . |
(3.2) |
k =k1 |
k =k1 |
|
Вероятность Pn (1 ≤ k ≤ n) того, что в n опытах событие А появится хотя бы |
||
один раз, определяется формулой |
|
|
Pn (1 ≤ k ≤ n) = 1 − qn . |
(3.3) |
|
Пример 3.2. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.
Решение. По формуле (3.2) при n = 10, k1 = 4, k2 = 6 , p = q = 0,5 находим
P |
(4 ≤ k ≤ 6) |
= P |
|
(4) |
+ P |
(5) + P |
(6) = |
210 |
+ |
252 |
+ |
210 |
= 21 . |
||
|
|
|
|
||||||||||||
10 |
|
10 |
|
10 |
|
10 |
1024 |
1024 |
1024 |
32 |
|||||
Согласно формуле (3.3) получим |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||
P10 |
(1 ≤ k ≤ 10) |
= 1 |
|
1 |
10 |
1023 |
. ► |
|
|
|
|
|
|||
− |
= |
1024 |
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Пример 3.3. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности наивероятнейшего числа появления бракованных деталей среди 5 отобранных.
Решение. Вероятность изготовления бракованной детали p = 1 − 0,8 = 0,2 . Ис-
комые вероятности найдем по формуле Бернулли (3.1):
P (0) = C0 |
|
0,20 |
0,85 |
= 0,32768; |
P (3) = C3 |
0,23 0,82 |
= 0,0512; |
|||
5 |
|
5 |
|
|
|
|
5 |
5 |
|
|
P |
(1) = C1 |
0,21 0,84 = 0,4096 ; |
P (4) = C 4 |
0,24 0,81 |
= 0,0064 ; |
|||||
5 |
|
5 |
|
|
|
|
5 |
5 |
|
|
P |
(2) |
= C 2 |
0,22 |
0,83 |
= 0,2048 ; |
P (5) = C5 |
0,25 0,80 |
= 0,00032 . |
||
5 |
|
5 |
|
|
|
|
5 |
5 |
|
|
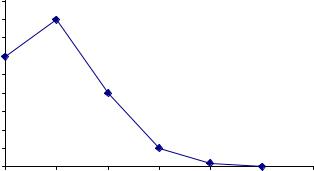
Полученные вероятности изобразим графически точками с координатами
(k, Pn (k)) . Соединяя эти точки, получим многоугольник, или полигон, распреде-
ления вероятностей (рис.9.).
0,45 |
P n (k ) |
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
0,35 |
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
0,25 |
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
0,15 |
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
k |
6 |
|
|
|
Рис. 9. |
|
|
|
|

31
Рассматривая многоугольник распределения вероятностей (рис.9), мы ви-
дим, что есть такие значения k (в данном случае оно одно — k0 = 1) обладающие наибольшей вероятностью. ►
Число k0 наступления события A в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Pn (k0 ) по крайней мере не меньше вероятностей других событий Pn (k) при любом k.
При заданных n и p это число определяется условиями:
np − q ≤ k0 ≤ np + p , k0 – целое число. |
(3.4) |
Если число np + p не является целым, то k0 равно целой части этого числа |
|
( k0 = [np + p]), если же np + p — целое число, то k0 |
имеет два значения |
k0' = np − q и k0'' = np + p .
Пример 3.4. По данным примера 3.3 найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.
Решение. По формуле (3.4) 0,2 ≤ k0 ≤ 1,2 . Очевидно, что единственное целое число, удовлетворяющее полученному неравенству, k0 = 1. Его вероятность P5 (1) = 0,4096 вычислена в примере 3.3. ►
Пример 3.5. Какова вероятность наступления события A в каждом испытании, если наивероятнейшее число наступлений события A в 120 опытах равно 32?
Решение. По условию n = 120, k0 = 32 . Неравенства (3.4) принимают вид
120 p − (1 − p) ≤ 32 ≤ 120 p + p .
Решая эту систему неравенств, находим, что 12132 ≤ p ≤ 12133 . ►
Пример 3.6. При стрельбе по мишени вероятность попадания при одном выстреле
равна 0,7. При каком числе выстрелов наивероятнейшее число попаданий равно
16?
Решение. По условию p = 0,7 q = 0,3 , k0 = 16 .
По формуле (3.4) найдем n.
|
2 |
|
n ≤ 23 |
|
7 . |
Из неравенств 0,7n − 0,3 ≤ 16 ≤ 0,7n + 0,7 получаем, что |
6 |
|
n ≥ 21 |
7 |
|
|
|
Итак, n1 = 22 , n2 = 23, т.е. число всех выстрелов может быть 22 или 23. ►
Пример 3.7. Предположим, что из озера вылавливают 1000 рыб, помечают их красной краской и выпускают обратно. При повторном отлове 1000 рыб среди них оказалось 100 помеченных. Можно ли определить число рыб в озере?

32
Решение. Если предположить, что было произведено 1000 испытаний, в каждом из которых либо появилась, либо не появилась помеченная рыба и считать число 100 (число помеченных рыб) наивероятнейшим числом помеченных рыб, то неравенства (3.4) позволят ответить положительно на поставленный вопрос.
Пусть N – число рыб в озере. Тогда p = 1000 |
N |
, n = 1000, k |
0 |
= 100 . |
|||
|
|
|
|
|
|
||
100 ≤ 10011000 |
|
|
|||||
|
|
|
|
N |
. |
|
|
Получаем систему неравенств |
|
|
|
|
|||
1000 |
|
|
1000 |
|
|||
|
− (1 − |
) ≤ 100 |
|
|
|||
1000 |
N |
N |
|
|
|||
Откуда 9891 ≤ N ≤ 10010 .
Т.о., мы нашли границы, в которых находится число рыб в озере. ►
3.2. Формула Пуассона
При большом числе испытаний n формулой Бернулли пользоваться неудобно, например, вычислить трудно P300 (250) = C300250 p250q50 . В этом случае вероятно-
сти того, что в n испытаниях (n – велико) событие произойдет k раз определяется приближенными формулами, которые устанавливается теоремами Пуассона, локальной и интегральной теоремами Муавра-Лапласа.
Теорема Пуассона. Если при большом числе испытаний n ( n → ∞ ) вероятность p появления А в одном опыте стремится к нулю ( p → 0 ), а произведение
пр = λ сохраняет постоянное значение для разных серий опытов (т. е. среднее число появлений события А в разных сериях испытаний остается неизменным), то вероятность Pn (k) удовлетворяет предельному равенству
lim Pn (k) = |
λk |
e−λ . |
(3.5) |
||
n→∞ |
|
|
k! |
|
|
Из предельного равенства (3.5) при больших n |
и малых p вытекает при- |
||||
ближенная формула Пуассона |
|
|
|
|
|
Pn ( k ) ≈ |
λk |
e−λ |
, |
λ = np. |
(3.6) |
|
k! |
|
|
|
|
Пример 3.8. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
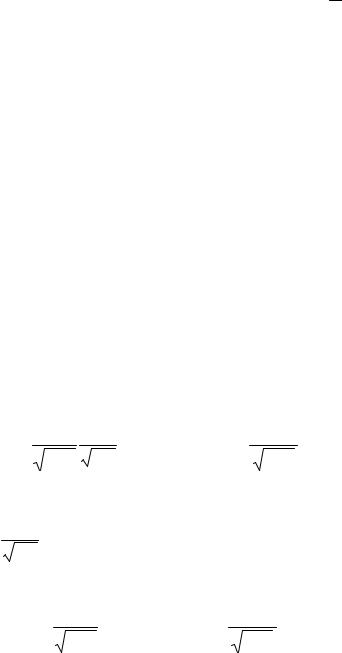
Решение. По условию n=1000, p=0,002, λ=np=2, k=3.
Искомая вероятность P1000 (3) = λ3 e−λ = 232 = 0,18 . ► 3! 2e
33
Пример 3.9. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
Решение. По условию n=500, p=0,004, следовательно, λ=2. По теореме сложения вероятностей
P500 (k < 3) = P500 (0) + P500 (1) + P500 (2) = e−2 + 12!e−2 + 24!e−2 = 5e−2 = 0,68. ►
Пример 3.10. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
Решение. λ=np=1000·0,003=3.
P1000 (k > 2) = 1− P1000 (k ≤ 2) = 1− (P1000 (0) + P1000 (1) + P1000 (2)) =
=1 − (e−3 + 3e−3 + 4,5e−3 )= 0,5678 . ►
3.3.Локальная и интегральная теоремы Муавра-Лапласа
Втех случаях, когда число испытаний п велико, а вероятности р не близка к нулю, для вычисления биномиальных вероятностей используют теоремы МуавраЛапласа.
Локальная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико, то вероятность Рп(k) может быть вычислена по приближенной формуле
P (k ) ≈ |
1 |
|
|
1 e− |
x2 |
, где x = k − np . |
(3.7) |
|
|
|
2 |
||||||
n |
|
npq |
2π |
|
npq |
|
||
|
|
|
|
|||||
Равенство (3.7) тем точнее, чем больше п. |
|
|||||||
|
1 |
e− |
x2 |
|
|
|
|
|
Выражение |
2 |
|
= ϕ (x) |
называется функцией Гаусса. |
|
|||
|
2π |
|
|
|
|
|
|
|
Равенство (3.7) можно переписать в виде |
|
|||||||
|
P (k ) ≈ |
1 |
ϕ (x), |
где x = k − np . |
(3.8) |
|||
|
n |
|
npq |
|
npq |
|
||
|
|
|
|
|
||||
Для функции ϕ (x) составлены таблицы значений (см. приложение 1). Пользуясь таблицей, следует учитывать, что:
а) функция ϕ (x) четная, т.е. ϕ (−x) = ϕ (x) ;
б) при x ≥ 4 можно считать, что ϕ (x) = 0.
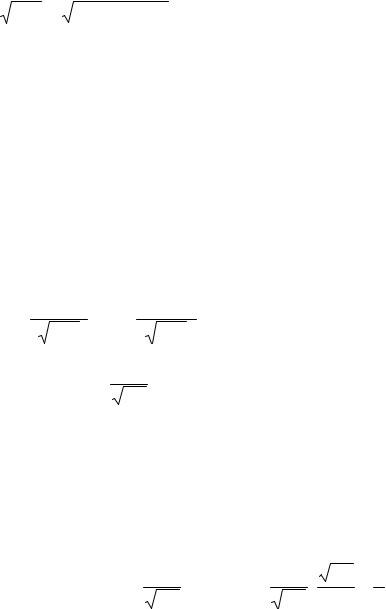
34
Пример 3.11. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение. Здесь п = 200, р = 0,7, q = 0,3, k=160. Применим формулу (3.8). Име-
ем: npq = 200 0,7 0,3 ≈ 6,48, следовательно, x = |
160 − 200 0,7 |
≈ 3,09 . Учиты- |
|||
|
|
|
|
6,48 |
|
вая, что ϕ (3,09) ≈ 0,0034, получаем P |
(160) ≈ |
1 |
0,0034 ≈ 0,0005 . ► |
||
|
|||||
200 |
6,48 |
|
|
|
|
|
|
|
|
||
В тех случаях, когда требуется вычислить вероятность того, что в п независимых испытаниях событие А появится не менее m1 раз, но не более m2 раз, т.е.
Pn (m1 ≤ k ≤ m2 ) , используют интегральную теорему Муавра-Лапласа (является частным случаем более общей теоремы — центральной предельной теоремы).
Интегральная теорема Муавра-Лапласа. Если вероятность p наступления со- |
||||||||||
бытия A в каждом испытании постоянна и отлична от нуля и единицы, то веро- |
||||||||||
ятность Pn (m1 ≤ k ≤ m2 ) может быть найдена по приближенной формуле |
||||||||||
|
|
|
Pn (m1 ≤ k ≤ m2 ) ≈ Φ0 (x2 )− Φ0 (x1), |
(3.9) |
||||||
гдеx1 = |
m1 |
− np |
, x2 |
= |
m2 |
− np |
, |
|
||
|
npq |
|
npq |
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
x |
|
t 2 |
|
|
|
|
Φ0 (x) = |
∫e− |
|
dt — нормированная функция Лапласа. |
(3.10) |
|||||
|
2 |
|||||||||
|
|
|
|
2π 0 |
|
|
|
|
|
|
Укажем некоторые свойства функции Φ0 (x) . |
|
|||||||||
1. |
|
Φ0 (x) |
определена при всех значениях x (−∞,+∞) . |
|
||||||
2.Φ0 (0) =0.
|
|
1 |
+ ∞ |
e− |
t 2 |
1 |
|
2π |
|
1 |
|
|
3. |
Φ0 (+∞) = |
∫ |
2 |
dt = |
|
= |
(при x ≥ 5 можно считать, |
|||||
|
|
2π |
0 |
|
|
|
2π |
|
2 |
|
2 |
|
что Φ0 (x) = 12 ).
4.Φ0 (−∞) = − 12 .
5.Φ0 (x) монотонно возрастает при всех x (−∞,+∞) .
6.Φ0 (x) – функция нечетная: Φ0 (− x) = −Φ0 (x) .
Наряду с нормированной функцией Лапласа (3.10) используют функцию
35
|
1 |
x |
− |
t2 |
(3.11) |
|
Φ(x) = |
∫ e |
2 |
dt , |
|||
|
2π |
−∞ |
|
|
|
|
называемую также функцией Лапласа. Она связана с функцией Φ0 (x) формулой
|
|
|
|
|
Φ(x) = 0,5 + Φ0 (x) . |
(3.12) |
|
|
Тогда формулу (3.9) можно записать в виде |
|
|||||
|
|
|
Pn (m1 ≤ k ≤ m2 ) ≈ Φ(x2 )− Φ(x1 ), |
(3.13) |
|||
гдеx1 |
= |
m1 − np |
, x2 = |
m2 |
− np |
. |
|
npq |
|
npq |
|
||||
|
|
|
|
|
|
||
Имеются таблицы приближенных значений функций Φ0 (x) и Φ(x) (инте-
грал не берется в элементарных функциях), которые приводятся в большинстве учебников по теории вероятностей (см. также приложение 2).
Пример 3.12. . Известно, что при контроле бракуется 10% изделий. На контроль отобрано 625 изделий. Какова вероятность того, что среди отобранных не менее 550 и не более 575 стандартных изделий?
Решение. По условию, n=625; p=0,9; q=0,1; k1=550; k2=575.
Искомую вероятность находим по формуле (3.9). Имеем
|
|
575 − 562,5 |
|
|
550 − 562,5 |
|
|
|
P625 |
|
|
|
|
|
|
≈ |
|
(550 ≤ m ≤ 575) ≈ Ф0 |
625 0,9 0,1 |
|
− Ф0 |
625 0,9 0,1 |
|
► |
||
|
|
|
|
|
|
Ф0 (1,67)− Ф0 (− 1,67) ≈ 0,4526 + 0,4526 = 0,9052.
4.Геометрическое определение вероятности
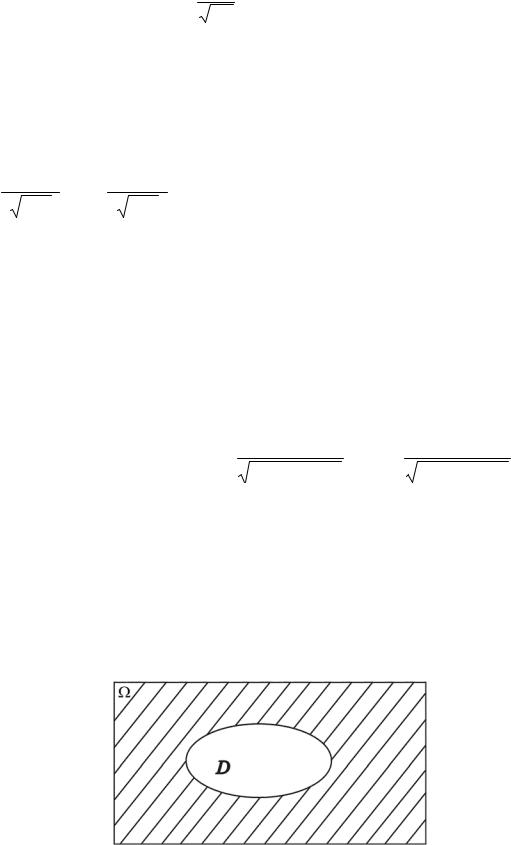
Впредыдущих разделах мы рассматривали лишь конечные ПЭС. Когда ПЭС (или Ω ) есть несчетное множество может применяться геометрическое определение вероятности. Рассмотрим на плоскости некоторую область Ω , имеющую площадь SΩ , и внутри области Ω область D с площадью SD (см. рис.10).
Рис.10.
В области Ω случайно выбирается точка X. Этот выбор можно интерпретировать как бросание точки X в область Ω . При этом попадание точки в область
36
Ω — достоверное событие, в D — случайное. Предполагается, что все точки области Ω равноправны (все элементарные события равновозможны), т. е. что брошенная точка может попасть в любую точку области Ω и вероятность попасть в область D пропорциональна площади этой области и не зависит от ее расположения и формы. Пусть событие А = { X D }, т. е. брошенная точка попадет в область D.
Геометрической вероятностью события А будем называть отношение
площади области D к площади области Ω , т. е. P( A) = SD . SΩ
Геометрическое определение вероятности события применимо и в случае,
когда области Ω и D обе линейные или объемные. В первом случае P(A) = lD , во lΩ
втором случае P(A) = VD , где l — длина, V — объем соответствующей области.
VΩ
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события A, к мере всей области, т.е..
P(A) = mesD |
(4.1) |
mesΩ |
|
Геометрическая вероятность обладает всеми свойствами классического определения вероятности.
Пример 4.1. Задача о встрече. Два лица условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
Решение. Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть x и y — моменты прихода первого и второго лица соответственно(точки отрезка [0,1]).Все возможные результаты эксперимента — это множество точек квадрата со стороной 1:
Ω = {(x, y): 0 ≤ x ≤1, 0 ≤ y ≤1 } (см. рис. 11).
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества
A = {( x , y): │x - y│ ≤ 1/6 } (лица встретятся, если разность между моментами их прихода будет не более 10 минут = 1/6 часа). То есть попадание во множество A наудачу брошенной в квадрат точки означает, что лица встретятся.
