
Теория_игр_методичка
.pdf41
Найденные значения заносим в третий столбец (ММ) и выбираем максимальное W max{ 3; 1; 7} 1, значит оптимальной по данному критерию является стратегия
А2 – продавать в зимние месяцы.
4. Критерий пессимизма-оптимизма Гурвица (П-О)
Для каждой строки рассчитываем значение критерия по формуле:
Wi С minaij (1 С) maxaij . По условию C 0,4 , значит: |
|
1 j 3 |
1 j 3 |
W1 0,4 min{2; 3; 7} (1 0,4) max{2; 3; 7} 0,4 ( 3) 0,6 7 1,2 4,2 3; W2 0,4 min{ 1; 5; 4} (1 0,4) max{ 1; 5; 4} 0,4 ( 1) 0,6 5 0,4 3 2,6;
W3 0,4 min{ 7; 13; 3} (1 0,4) max{ 7; 13; 3} 0,4 ( 7) 0,6 13 2,8 7,8 5 .
Найденные значения заносим в четвертый столбец (П-О) и выбираем максимальное W max{3; 2,6; 5} 5 , значит оптимальной по данному критерию является стратегия А3 –
продавать в весенние месяцы.
5. Критерий Ходжа-Лемана (Х-Л)
Для каждой строки рассчитываем значение критерия по формуле:
3 |
|
Wi u aij p j (1 u) minaij . По условию u 0,6 и множители в каждом слагаемом уже |
|
j 1 |
1 j 3 |
|
|
рассчитаны, их можно взять их первого столбика (Б) и из третьего столбика (ММ), значит:
W1 0,6 1 (1 0,6) ( 3) 0,6 1,2 0,6 ; W2 0,6 3,5 0,4 ( 1) 2,1 0,4 1,7 ;
W3 0,6 4,2 0,4 ( 7) 2,52 2,8 0,28.
Найденные значения заносим в пятый столбец (Х-Л) и выбираем максимальное W max{ 0,6; 1,7; 0,28} 1,7 , значит оптимальной по данному критерию является
стратегия А2 – продавать в зимние месяцы.
5. Критерий минимаксного риска Сэвиджа
Рассчитаем матрицу рисков. Заполнять ее лучше по столбцам. В каждом столбце находим максимальный элемент и вы читаем из него все остальные элементы столбца, результаты записываем на соответствующих местах.
Вот как рассчитывается первый столбец. Максимальный элемент в первом столбце: a11 2 , значит по формуле rij maxi aij aij :
r11 2 a11 2 2 0 ; r21 2 a21 2 ( 1) 3 ; r31 2 a31 2 ( 7) 9 .
Рассчитаем второй столбец матрицы рисков. Максимальный элемент во втором столбце: a32 13, значит:
r12 13 a12 13 ( 3) 16 ; r22 13 a22 13 5 8 ;
r32 13 a32 13 13 0 .
Рассчитаем третий столбец матрицы рисков. Максимальный элемент в третьем столбце: a13 7 , значит:
r13 7 a13 7 7 0 ; r23 7 a23 7 4 3;
r33 7 a33 7 ( 3) 10 .

42
Таким образом, матрица рисков имеет вид (в каждом столбце на месте максимального элемента платежной матрицы должен стоять ноль):
|
|
|
|
|
Wi |
0 |
|
16 |
|
0 |
16 |
3 |
8 |
3 |
8 |
||
9 |
0 |
10 |
10 |
||
Дополним матрицу рисков рассчитанными значениями критерия Wi – в каждой
строке выбираем максимальный элемент (Wi maxrij ):
j
W1 max{0; 16; 0} 16 ; W2 max{3; 8; 3} 8; W3 max{9; 0; 10} 10 ;
Найденные значения заносим в столбец (Wi) и выбираем минимальное
W min{16; 8; 10} 8 , значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
Вывод:
1)Стратегия А1 (продавать сразу после уборки) не является оптимальной ни по одному из критериев.
2)Стратегия А2 (продавать в зимние месяцы) является оптимальной согласно критериям недостаточного основания Лапласа, максиминного критерия Вальда и минимаксного критерия Сэвиджа.
3)Стратегия А3 (продавать в весенние месяцы) является оптимальной согласно критериям Байеса, пессимизма-оптимизма Гурвица, Ходжа-Лемана.
Заданиена самостоятельнуюработу
Задания по вариантам (N – номер варианта; N = 1, …, 30)
Сельскохозяйственное предприятие планирует посадить некоторую сельскохозяйственную культуру двух сортов. Посевная площадь 1000 га. Сорта отличаются друг от друга требованиями к влаге во время вегетационного периода. Проанализировав погодные условия, выделены 4 состояния погоды (S1, S2, S3, S4), отличающиеся режимом осадков и найдены статистические вероятности каждого состояния: p1=0.1; p2=0.3; p3=0.4; p4=0.2. Средняя урожайность (ц/га) каждого сорта на всем участке для каждой состояния погоды приведена в таблице:
|
S1 |
S2 |
S3 |
S4 |
Сорт 1 |
23+N |
29+N |
31+N |
37+N |
Сорт 2 36+N 33+N 28+N 24+N
Возможные варианты посева:
А1) сорт 1 посадить на 100% площади; А2) сорт 1 посадить на 75% площади, сорт 2 посадить на 25% площади;
А3) сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади; А4) сорт 1 посадить на 25% площади, сорт 2 посадить на 75% площади; А5) сорт 2 посадить на 100% площади; Определить оптимальную стратегию с помощью критериев максимального
математического ожидания, недостаточного основания Лапласа, максиминного критерия Вальда, пессимизма-оптимизма Гурвица (коэффициент пессимизма взять равным 0,4), критерия Ходжа-Лемана (коэффициент достоверности информации о состояниях погоды принять равным 0,7), критерия минимаксного риска Сэвиджа.
43
8. Метод идеальной точки решения линейных двухкритериальных задач оптимизации
Решение типового примера
Множество допустимых решений на плоскости xOy задано системой линейных неравенств. Найти допустимое решение, при котором достигают максимума две линейные функции U(x, y), V(x, y).
Система неравенств:
4y – x ≤ 20; 4x + y ≤ 22; х – у ≤ 3; х ≥ 0; у ≥ 0
Целевые функции:
U = 2х – 2у → max V = –2x – y → max
Решение
1. Построим область допустимых решений (ОДР) в плоскости xOy, определяемую системой неравенств. Каждое линейное неравенство на плоскости задает полуплоскость, все точки которой обращают неравенство в верное числовое неравенство.
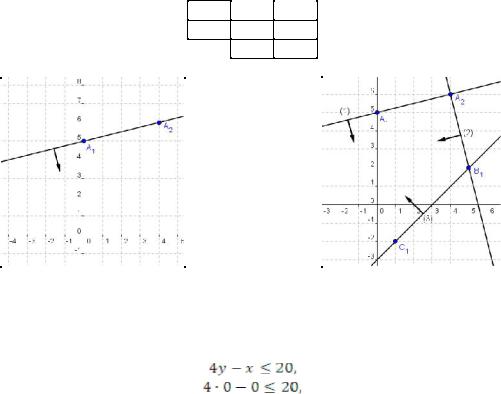
Рассмотрим первое неравенство 4y – x ≤ 20.
Границей полуплоскости является прямая 4y – x = 20. Построим эту прямую по двум точкам. Составим таблицу и выполним построение (рис. 1):
x 0 4
y 5 6
A1 A2
|
|
|
Рис. 1 |
|
Рис. 2 |
Определим, какую полуплоскость задает первое неравенство: выше построенной прямой или ниже ее. Для этого подставим в неравенство координаты любой точки, не лежащей на построенной прямой. Обычно берут начало координат: (0; 0):



 .
.
Получили верное числовое неравенство, значит рассматриваемое линейное неравенство определяет полуплоскость, которой принадлежит начало координат, т.е. расположенную ниже построенной прямой (рис. 1).
Аналогично определим полуплоскости, задаваемые вторым и третьим неравенствами: 4x + y ≤ 22 и х – у ≤ 3 (рис. 2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
||
2) |
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
|
x |
5 |
4 |
|
x |
5 |
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
2 |
|
6 |
|
|
|
|
|
y |
|
2 |
|
-2 |
|
Оставшиеся ограничения: |
|
B1 |
|
A2 |
|
задают |
|
|
B1 |
|
C1 |
|
||||||
|
х ≥ 0, у ≥ 0 |
первую |
|
координатную четверть. |
||||||||||||||
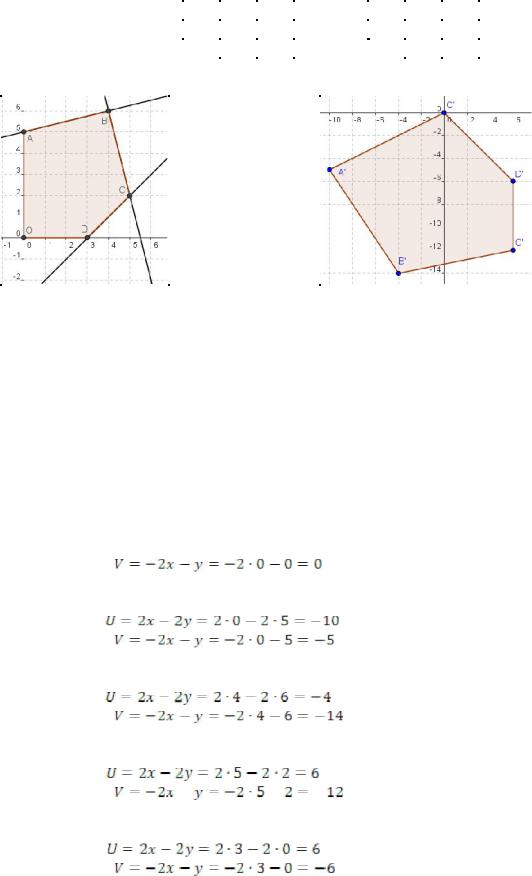
Область допустимых решений изображена на рисунке 3 – многоугольник OABCD.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Рис. 3 |
|
|
Рис. 4 |
|||||||
|
2. Построим в критериальной |
плоскости область, соответствующую области |
|||||||||
допустимых решений OABCD. Для этого необходимо найти координаты вершин.
В нашем случае очевидно, что O(0; 0), A(0; 5), B(4; 6), C(5; 2), D(3; 0), т.к. часть этих точек использовалась при построении прямых. В общем случае координаты точки пересечения двух прямых определяют совместным решением их уравнений, например, для точки С = B1, которая является точкой пересечения (2) и (3) прямых (рис. 2):
С (2) |
4x y 22, |
5x 25, |
x 5, |
(3) : |
|
|
|
|
x y 3, |
x y 3, |
y 2. |
Найдем координаты образов точек O, A, B, C, D в линейном преобразовании, определяемом целевыми функциями:
O(0; 0): 















Таким образом, O(0; 0) → O(0; 0).
A(0; 5):
Таким образом, A(0; 5) → A(–10; –5).
B(4; 6):
Таким образом, B(4; 6) → B(–4; –14).
C(5; 2):
Таким образом, C(5; 2) → C(6; –12).
D(3; 0):
Таким образом, D(3; 0) → D(6; –6).
По найденным координатам точек построим в критериальной плоскости UOV образ многоугольника OABCD – многоугольник O A B C D (рис. 4).
45
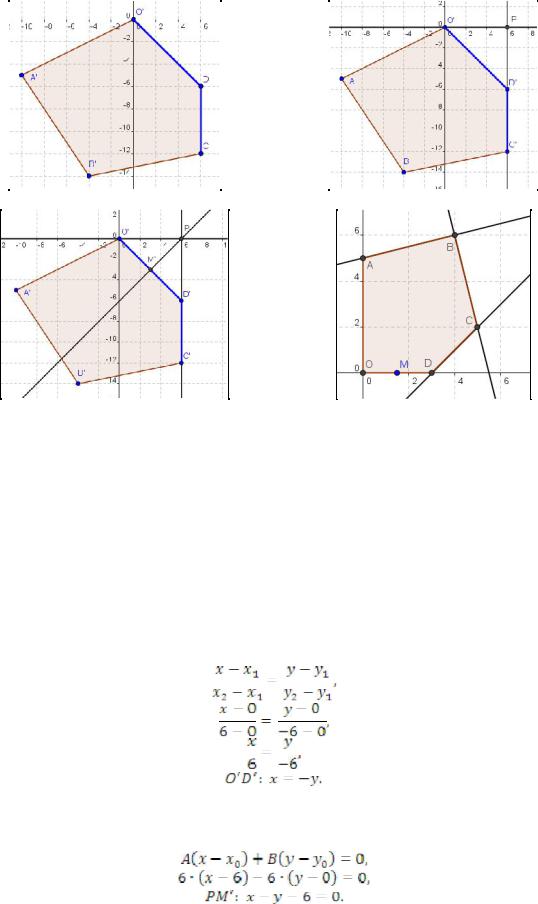
3. В критериальной плоскости найдем границу Парето – северо-восточную границу области O A B C D.
|
|
|
|
|
|
|
|
Рис. 5 |
|
|
|
Рис. 6 |
|
Рис. 7 |
|
Рис. 8 |
Точкой утопии, в которой достигается максимум одновременно по двум критериям U и V, является точка P (рис. 6): через самую высокую (северную) точку области
O A B C D провели горизонтальную прямую (через точку O) и через самую правую (восточную) точку области O A B C D провели вертикальную прямую (через точки C и D); точка – точка пересечения горизонтальной и вертикальной прямой.
4. На границе Парето найдем идеальную точку – точку, наиболее близко расположенную к точке утопии. В нашем случае это основание перпендикуляра,
опущенного из точки утопии Р на отрезок O D – точка M (рис. 7).
Найдем координаты точки M. Для этого найдем уравнение прямой O D. Воспользуемся уравнением прямой, проходящей через две точки:
O(0; 0), D(6; –6)
Найдем уравнение перпендикуляра, опущенного из точки утопии P на отрезок O D. Воспользуемся уравнением прямой с точкой и вектором нормали:


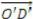

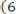




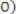

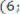
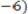 ,
, 
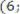

46
Координаты точки М:
Т.е.: М(3; –3), а значит компромиссное решение позволит достигнуть значений целевых функций: U = 3, V = –3.
5. Найдем координаты точки в плоскости xOy, которой соответствует точка М критериальной плоскости. Для этого решим систему уравнений:
Получили, что компромиссным решением метода идеальной точки является M(1,5; 0), в которой критерии достигают значений U = 3, V = –3.
Эта точка принадлежит отрезку OD (рис. 8). Ответ: M(1,5; 0), U = 3, V = –3.
Заданиена самостоятельнуюработу
Множество допустимых решений на плоскости xOy задано системой линейных неравенств. Найти допустимое решение, при котором достигают максимума две линейные функции U(x, y), V(x, y).
Вариант 1
Система неравенств:
х– 3y ≥ –15; 2x + y ≤ 12;
х– у ≤ 3; х ≥ 0; у ≥ 0 Целевые функции:
U = –5х + 3у → max V = 10x + 3y → max
Вариант 3
Система неравенств:
х – 2y ≥ –8; 3x + y ≤ 18; 3х – 2у ≤ 9; х ≥ 0; у ≥ 0
Целевые функции:
U = –9х + 3у → max V = x – 2y → max
Вариант 5
Система неравенств:
х – y ≥ –3; 2x + 3y ≤ 19; 3х – 2у ≤ 9; х ≥ 0; у ≥ 0
Целевые функции:
U = –4х – у → max V = –7x + 6y → max
Вариант 7
Система неравенств:
х– y ≥ –3; x + 5y ≤ 27;
х– у ≤ 3; х ≥ 0; у ≥ 0 Целевые функции:
U = 6х + 2у → max V = –5x + 6y → max
Вариант 2
Система неравенств:
х– 2y ≥ –8; 4x + y ≤ 22;
х– у ≤ 3; х ≥ 0; у ≥ 0 Целевые функции:
U = х – у → max V = –4x + y → max
Вариант 4
Система неравенств:
х – y ≥ –4; x + y ≤ 8; 3х – 2у ≤ 9; х ≥ 0; у ≥ 0
Целевые функции:
U = –2х + 5у → max V = –6x + 3y → max
Вариант 6
Система неравенств:
х– y ≥ –3; x + 2y ≤ 12;
х– у ≤ 3; х ≥ 0; у ≥ 0 Целевые функции:
U = 4х + 10у → max V = 2x – 9y → max
Вариант 8
Система неравенств:
х – y ≥ –2; 2x + 5y ≤ 24; 2х – 3у ≤ 8; х ≥ 0; у ≥ 0
Целевые функции:
U = 9х + 8у → max V = 3x – 10y → max
Вариант 9
Система неравенств:
х – y ≥ –2; x + y ≤ 8; 2х – у ≤ 10; х ≥ 0; у ≥ 0
Целевые функции:
U = 2х – 6у → max V = –4x – 8y → max
Вариант 11
Система неравенств:
3y – 2x ≤ 6; 2x + y ≤ 10; х – у ≤ 2; х≥0; у≥0
Целевые функции:
U=-4х + 3у → max V=-3x – 6y → max
Вариант 13
Система неравенств:
2y – 3x ≤ 2; 2x – 3y ≤ 4; 2x + 3y ≤ 16; х≥0; у≥0
Целевые функции:
U = 4х + 3у → max V = -x + 4y → max
Вариант 15
Система неравенств:
y – 2x ≤ 1; 2y – x ≤ 8; 6x + y ≤ 30; х≥0; у≥0
Целевые функции:
U = х + 2у → max V = -3x + 2y → max
Вариант 17
Система неравенств:
y – 2x ≤ 3; 4y – x ≤ 19; 3x + y ≤ 21; х≥0; у≥0
Целевые функции:
U = 3х + 8у → max V = -6x + 2y → max
Вариант 19
Система неравенств:
y – x ≤ 2; x + 2y ≤ 10; 3x – y ≤ 9; х≥0; у≥0
Целевые функции:
U = 5х + у → max V = -2x + 3y → max
47
Вариант 10
Система неравенств:
2х – 3y ≥ –6; 2x + 5y ≤ 26; х – у ≤ 6; х ≥ 0; у ≥ 0
Целевые функции:
U = –4х – 6у → max V = 8x – 6y → max
Вариант 12
Система неравенств:
y – x ≤ 3; 4y – x ≤ 15; 5x + 2y ≤ 35; х≥0; у≥0
Целевые функции:
U = 4х + 8у → max V = -6x + 3y → max
Вариант 14
Система неравенств:
3y – 2x ≤ 6; x + y ≤ 7; x – y ≤ 3; х≥0; у≥0
Целевые функции:
U = 3х – у → max V = -x + 4y → max
Вариант 16
Система неравенств:
3y – x ≤ 15; x – 2y ≤ 3; x + y ≤ 9; х≥0; у≥0
Целевые функции:
U = х – 3у → max V = -2x – y → max
Вариант 18
Система неравенств:
x + y ≤ 4; x – y ≤ 2; x + 2y ≤ 6; х≥0; у≥0
Целевые функции:
U = 3х + 4у → max V = -x + 2y → max
Вариант 20
Система неравенств:
3y – 4x ≤ 3; 3y – x ≤ 12; 6x – y ≤ 30; х≥0; у≥0
Целевые функции:
U = х + у → max V = -3x + 3y → max
Вариант 21
Система неравенств:
4y – x ≤ 20; 2x + y ≤ 14; 2x – 3y ≤ 6; х≥0; у≥0
Целевые функции:
U = 2х – 3у → max V = -2x – 2y → max
Вариант 23
Система неравенств:
2y – x ≤ 6; 3x + 2y ≤ 14; x – 2y ≤ 2; х≥0; у≥0
Целевые функции:
U = 3х + у → max V = x + 2y → max
Вариант 25
Система неравенств:
y – 2x ≤ 1; 2x + 3y ≤ 27; 5x – y ≤ 25; х≥0; у≥0
Целевые функции:
U = 2х – 2у → max V = -4x – y → max
Вариант 27
Система неравенств:
3y – 2x ≤ 12; 2x + 3y ≤ 24; 4x + y ≤ 28; х≥0; у≥0
Целевые функции:
U = 6х + 3у → max V = -2x + 4y → max
Вариант 29
Система неравенств:
2y – 3x ≤ 4; 2y – x ≤ 8; 6x – y ≤ 18; х≥0; у≥0
Целевые функции:
U = 4х + 2у → max V = -3x + 2y → max
48
Вариант 22
Система неравенств:
y – x ≤ 3; 4y – x ≤ 18; 6x + y ≤ 42; х≥0; у≥0
Целевые функции:
U = 3х + 3у → max V = -3x + 4y → max
Вариант 24
Система неравенств:
y – x ≤ 2; x + y ≤ 8; 3x – 2y ≤ 9; х≥0; у≥0
Целевые функции:
U = 3х – у → max V = -2x + 4y → max
Вариант 26
Система неравенств:
x + 4y ≤ 20; 3x + 2y ≤ 20; x – 3y ≤ 3; х≥0; у≥0
Целевые функции:
U = х – 4у → max V = -x – y → max
Вариант 28
Система неравенств:
3y – x ≤ 9; x + y ≤ 7; 2x – 3y ≤ 4; х≥0; у≥0
Целевые функции:
U = 3х – у → max V = x + 4y → max
Вариант 30
Система неравенств:
3y – 4x ≤ 3; 3x + 4y ≤ 29; x – y ≤ 5; х≥0; у≥0
Целевые функции:
U = 2х – 3у → max V = -2x – y → max
