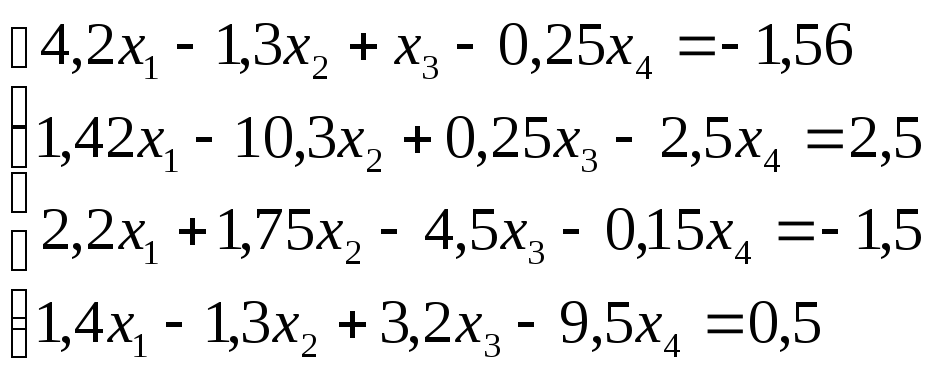16

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный строительный университет»

Утверждено на заседании

кафедры высшей математики

«28» августа 2012г.

Методические указания

по дисциплине «Информатика»

к лабораторной работе по теме:

Матричные операции и решение СЛАУ в MS Excel

для обучающихся на 1, 2-м курсах по

направлениям подготовки

190700 «Технология транспортных процессов»,

270800 «Строительство»,

280700 «Техносферная безопасность»

Часть 2

Ростов-на-Дону

2013

УДК 681.517.07

Методические указания по дисциплине «Информатика» к лабораторной работе по теме: «Матричные операции и решение СЛАУ в MS Excel» для обучающихся на 1, 2-м курсах по направлениям подготовки 190700 «Технология транспортных процессов», 270800 «Строительство», 280700 «Техносферная безопасность» . Часть 2.– Ростов н/Д : РГСУ, 2013. – 16 с.

В предлагаемых методических указаниях содержится материал, необходимый для освоения курса «Информатики» для обучающихся на технических направлениях подготовки (специальностях).

Методические указания содержат руководство по выполнению лабораторных работ, задания для самостоятельной работы студентов и приложение.

Электронная версия методических указаний находится в библиотеке, ауд. 224

УДК 681.517.07

Составители:	канд.физ.-мат.наук, доцент Л.А.Кладенок, канд.физ.-мат.наук, доцент О.В.Назарько, канд.физ.-мат.наук, доцент Н.А.Сайфутдинова, ассистент А.Н.Шишкова, ассистент С.К.Макаров
Рецензент:	канд.физ.-мат.наук, доцент С.А.Никитин

Редактор Н.А.Матекина

Темплан 2012 г., поз.89

Подписано в печать 19.04.13. Формат 60х84/16. Ризограф. Бумага писчая. Уч.-изд.л.0,7. Тираж 100 экз. Заказ

Редакционно-издательский центр Ростовского государственного строительного университета 344022, Ростов-на-Дону, ул. Социалистическая, 162.

© Ростовский государственный

строительный университет, 2012.

Итерационнные методы решения слау

Рассмотрим систему линейных алгебраических уравнений , где  матрица размерности ,  вектор решения, – вектор правых частей:

(1)

Численные методы решения данной системы принято разделять на два класса: прямые методы («точные») и итерационные.

Прямыми методами называются методы, позволяющие получить решение системы уравнений (1) за конечное число арифметических операций.

К прямым методам относятся метод Крамера, метод Гаусса и ряд других методов. Основным недостатком прямых методов является то, что для нахождения решения необходимо выполнить большое число операций.

Суть итерационных методов состоит в том, что решение системы (1) находится как предел последовательных приближений при , где  номер итерации. Применение итерационных методов требует задания начального значения неизвестных (обычно берут для i=1,2,…,m) и точности вычислений . Вычисления проводятся до тех пор, пока не будут выполнены оценки

.

Основное достоинство итерационных методов состоит в том, что точность искомого решения задается.

Различные итерационные методы отличаются формулами расчета очередного приближения. Для получения расчетных формул выполним следующие действия: из i-го уравнения системы (1) выразим x_i :

.

Эти равенства являются основными для расчетных формул методов Якоби и Зейделя.

Метод Якоби: (2)

Данная формула используется для вычисления последующего приближения по известному приближению,координаты которого поставляются в правую часть.

Метод Зейделя: .(3)

Особенностью метода Зейделя является то, что при вычислении используются уже полученные .

Условием сходимости метода Зейделя является диагональное преобладание матрицы , т.е.,i  j, (4) и хотя бы для одной строчки должно быть строгое неравенство. Для метода простой итерации условие может быть строгим, т.е. ,i  j (4.а)

Задание 1.

Решить систему линейных алгебраических уравнений : методом простой итерации (методом Якоби). Методом Зейделя. Точность для обоих методов . Проанализировать полученные результаты нахождения корней СЛАУ методом простой

Образец выполнения.