
- •Часть 1. Линейная алгебра
- •1.1.2. Линейные операции над матрицами
- •1.1.3. Умножение матриц
- •1.1.4.Определители
- •Свойства определителей
- •1.1.5. Обратные матрицы
- •1.2. Системы линейных алгебраических уравнений
- •1.2.1. Метод Крамера
- •1.2.2. Матричный метод
- •1.2.3. Метод Гаусса
- •1.3. Ранг матрицы
- •Свойства ранга матрицы
- •1.4. Собственные векторы и собственные значения матрицы
- •Задачи для самостоятельной работы
- •1.5. Примеры использования алгебраического аппарата для классических экономических моделей.
- •Задачи для самостоятельной работы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено
на заседании кафедры прикладной математики и вычислительной техники 20.05.2011 г.
Линейная алгебра (1 часть)
Методические указания для практических работ студентов
специальностей «Экономика предприятий и организаций, Финансы и кредит, Бухгалтерский учет, анализ и аудит, Налоги и налогообложения»
Ростов-на-Дону
2011
УДК 51(075.8)
Линейная алгебра (1 часть): методические указания для практических работ студентов специальностей «Экономика предприятий и организаций, Финансы и кредит, Бухгалтерский учет, анализ и аудит, Налоги и налогообложения»– Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 32 с.
Изложен краткий курс по линейной алгебре. Представлены типовые задачи и их решения. Приведены варианты заданий для самостоятельной работы. Предназначены для практических работ студентов как очной, так и заочной форм обучения специальностей «Экономика предприятий и организаций», «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Налоги и налогообложения», «Региональная экономика». Электронная версия методических указаний находится в библиотеке, ауд. 224.
УДК 51(075.8)
Составители:
к.ф.-м.н. Богачева М.Н.
к.ф.-м.н. Гробер О.В.
к.ф.-м.н. Гробер Т.А.
Редактор Н.Е. Гладких
Темплан 2011 г., поз.
Подписано
в печать Формат
![]() .
Бумага писчая. Ризограф.
.
Бумага писчая. Ризограф.
Уч.-изд.л. 1,7. Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162.
Ростовский государственный строительный университет, 2011
Часть 1. Линейная алгебра
Матрицы и определители
Основные понятия
Матрицей
размера
![]() называется прямоугольная таблица чисел,
содержащая
называется прямоугольная таблица чисел,
содержащая![]() строк
и
строк
и![]() столбцов
столбцов
 .
.
Каждый
элемент матрицы
![]() имеет два индекса:
имеет два индекса:![]() – номер строки и
– номер строки и![]() – номер столбца. Например, в матрице
– номер столбца. Например, в матрице

размера
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Часто
используется краткая запись матрицы:
![]() .
Матрица называетсяквадратной
.
Матрица называетсяквадратной
![]() -го
порядка, если она состоит из
-го
порядка, если она состоит из![]() строк и
строк и![]() столбцов. Матрица размера
столбцов. Матрица размера![]() называетсяматрицей-строкой,
а матрица размера
называетсяматрицей-строкой,
а матрица размера
![]() матрицей-столбцом.
матрицей-столбцом.
Нулевой матрицей О заданного размера называется матрица, все элементы которой равны 0.
Единичнойназывается квадратная матрица, элементы главной диагонали которой равны 1, а все остальные элементы равны 0:
 .
.
Можно говорить о единичных матрицах любого порядка.
Транспонированной
для матрицы
![]() называется матрица
называется матрица![]() ,
строки которой являются столбцами
матрицы
,
строки которой являются столбцами
матрицы![]() ,
а столбцы – строками
,
а столбцы – строками![]() .
Например, если
.
Например, если
![]() ,
то
,
то
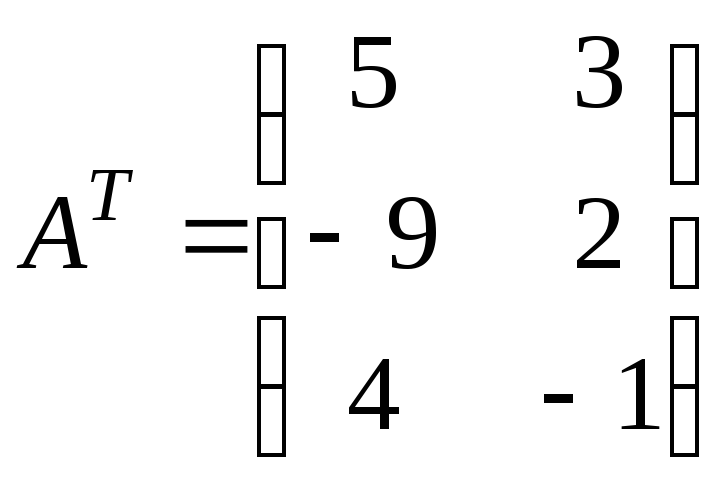 .
.
Матрицы
![]() и
и![]() называютсяравными,
если
называютсяравными,
если
![]() ,
,![]() ,
,![]() .
.
1.1.2. Линейные операции над матрицами
Суммой
матриц
![]() и
и![]() называется матрица
называется матрица![]() .
.
Другими словами, для сложения матриц надо сложить элементы матриц, стоящие на одних и тех же местах. Складываются матрицы только одинакового размера.
Произведениемматрицы![]() на число
на число![]() называется матрица
называется матрица![]() .
.
Другими словами, для умножения матрицы на число надо каждый элемент матрицы умножить на это число. Любую матрицу можно умножить на любое число.
Для любых матриц
одинакового размера и любых чисел
![]() и
и![]() выполняются свойства:
выполняются свойства:
|
1)
|
4)
|
|
2)
|
5)
|
|
3)
|
6)
|
Пример 1.Даны матрицы![]() и
и![]() .
Найти матрицу
.
Найти матрицу![]() .
.
Решение.
![]()
1.1.3. Умножение матриц
Матрицы умножаются по правилу «строка на столбец». Расшифруем, что имеется в виду.
Произведением
матрицы
![]() на матрицу
на матрицу![]() называется матрица
называется матрица![]() размера
размера![]() с элементами
с элементами![]() ,
,![]() ,
,![]() .
.
Другими
словами, для получения элемента, стоящего
в
![]() -той
строке и
-той
строке и![]() -том
столбце матрицы-произведения, следует
вычислить сумму произведений элементов
-том
столбце матрицы-произведения, следует
вычислить сумму произведений элементов![]() -той
строки матрицы
-той
строки матрицы![]() на
на![]() -тый
столбец матрицы
-тый
столбец матрицы![]() .
.
В самом определении произведения матриц заложено, что число столбцов первой матрицы должно совпадать с числом строк второй. Это условие согласования матриц при умножении. Если оно нарушено, то матрицы перемножить нельзя.
Пример
2. Найти
произведение матриц
![]() и
и![]() .
.
Решение.
![]() .
.
Заметим,
что вполне возможна ситуация, когда
![]() существует, а
существует, а![]() нет. Именно так происходит в примере 2.
Кроме того, когда существуют оба
произведения, то чаще всего они не равны,
т.е., вообще говоря,
нет. Именно так происходит в примере 2.
Кроме того, когда существуют оба
произведения, то чаще всего они не равны,
т.е., вообще говоря,![]() .
Приведем еще ряд свойств операции
умножения матриц. Если
.
Приведем еще ряд свойств операции
умножения матриц. Если![]() и
и![]() - квадратные матрицы одного порядка, то
справедливы равенства:
- квадратные матрицы одного порядка, то
справедливы равенства:
|
1)
|
3)
|
|
2)
|
4)
|
1.1.4.Определители
Понятие
определителя вводится только для
квадратных матриц. Рассмотрим квадратную
матрицу 2го
порядка:
 .
.
Определителем
2го
порядка матрицы
![]() называется число:
называется число:
![]() .
.
Пример
3. Вычислить
определитель матрицы
![]() .
.
Решение.
![]()
Пусть
 – матрица 3го
порядка.
– матрица 3го
порядка.
Минором
элемента
![]() называется определитель
называется определитель![]() ,
составленный из элементов, оставшихся
после вычеркивания из матрицы
,
составленный из элементов, оставшихся
после вычеркивания из матрицы![]() -той
строки и
-той
строки и![]() -того
столбца.
-того
столбца.
Алгебраическим
дополнением
элемента
![]() называется число
называется число
![]() .
.
Определителем
3го
порядка (матрицы
![]() )
называется сумма произведений элементов
первой строки матрицы на их алгебраические
дополнения.
)
называется сумма произведений элементов
первой строки матрицы на их алгебраические
дополнения.
 .
.
Пример
3. Вычислить
определитель матрицы
 .
.
Решение. Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:
![]() ;
;
![]() ;
;
![]() .
.
Вычисляем исходный определитель
![]()
В дальнейшем при вычислении определителей мы будем пользоваться более короткой записью:

Далее индуктивно вводится понятие определителей более высоких порядков.
Определителем
![]() -го
порядка
называется сумма произведений элементов
1-ой строки на их алгебраические
дополнения.
-го
порядка
называется сумма произведений элементов
1-ой строки на их алгебраические
дополнения.
